Whats 15 Percent Of 25
saludintensiva
Sep 11, 2025 · 5 min read
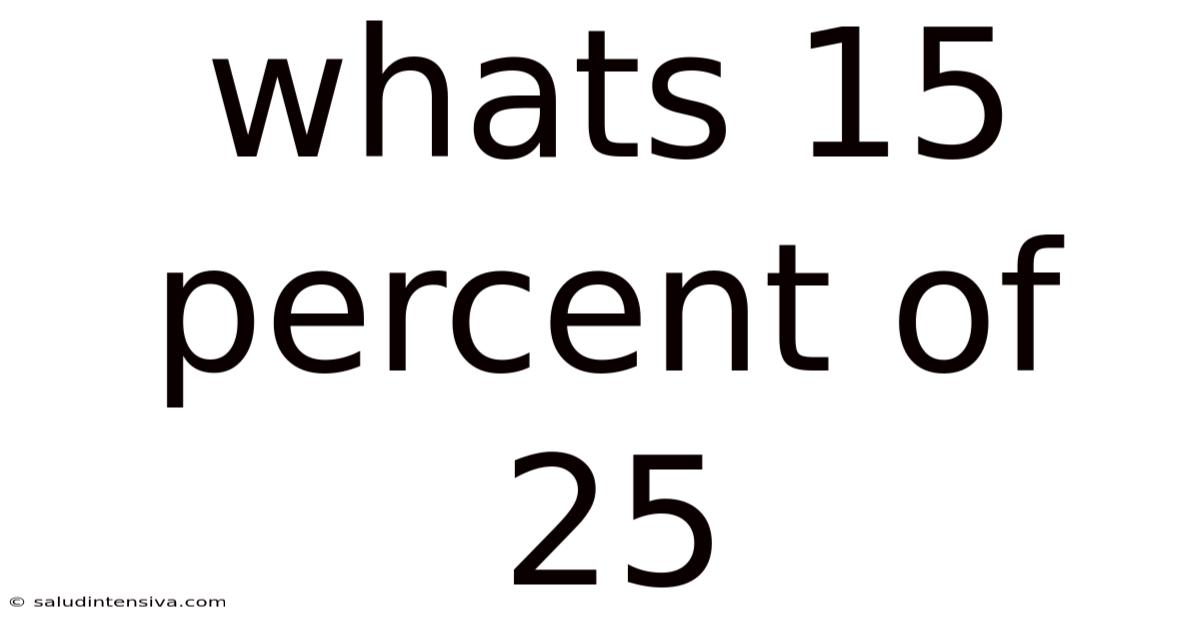
Table of Contents
What's 15 Percent of 25? A Deep Dive into Percentages and Their Applications
Finding 15% of 25 might seem like a simple calculation, easily solved with a calculator. However, understanding the underlying principles of percentages is crucial for various aspects of life, from calculating discounts and taxes to understanding financial reports and statistical data. This article will not only answer the question "What's 15 percent of 25?" but will also explore the concept of percentages in detail, providing you with the tools to tackle similar problems confidently and apply this knowledge in real-world scenarios.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The term "percent" literally means "out of one hundred" ("per cent" in Latin). So, 15% means 15 out of 100, or 15/100. This fraction can be simplified to 3/20. Understanding this fundamental concept is key to solving percentage problems.
Percentages are used extensively because they provide a standardized way to compare different quantities. Whether you're comparing the performance of two stocks, the success rate of two medical treatments, or the discount offered by two stores, percentages allow for a clear and easy comparison.
Calculating 15% of 25: Three Methods
There are several ways to calculate 15% of 25. Let's explore three common methods:
Method 1: Using the Fraction Method
As mentioned earlier, 15% can be expressed as the fraction 15/100. To find 15% of 25, we simply multiply 25 by this fraction:
25 * (15/100) = (25 * 15) / 100 = 375 / 100 = 3.75
Therefore, 15% of 25 is 3.75.
Method 2: Using Decimal Conversion
Percentages can also be expressed as decimals. To convert a percentage to a decimal, divide the percentage by 100. For 15%, this would be 15/100 = 0.15. Now, we can multiply 25 by 0.15:
25 * 0.15 = 3.75
This method provides the same result as the fraction method, confirming our answer.
Method 3: Using the Proportion Method
This method is particularly useful for understanding the relationship between the percentage, the whole, and the part. We can set up a proportion:
15/100 = x/25
Where 'x' represents the unknown value (15% of 25). To solve for x, we cross-multiply:
15 * 25 = 100 * x 375 = 100x x = 375 / 100 = 3.75
Again, we arrive at the same answer: 15% of 25 is 3.75.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is a valuable skill with numerous practical applications:
-
Shopping and Sales: Calculating discounts on sale items is a common application. If a shirt costs $25 and is on sale for 15% off, you'll save $3.75.
-
Taxes: Understanding sales tax percentages is essential for budgeting and calculating the final cost of purchases. If the sales tax is 6%, and you buy something for $25, the tax will be 6% of $25, or $1.50.
-
Finance: Percentages are fundamental to understanding interest rates, returns on investments, and loan repayments. Calculating compound interest, for instance, relies heavily on percentage calculations.
-
Statistics: Data analysis often involves working with percentages, such as calculating percentages of responses in surveys, the success rates of different treatments, or changes in population demographics.
-
Science: In scientific fields, percentages are used to express concentrations of solutions, error rates in experiments, and other quantitative relationships.
-
Everyday Life: Even everyday tasks like calculating tips at a restaurant, determining the percentage of ingredients in a recipe, or figuring out the proportion of a budget allocated to different expenses involve percentage calculations.
Beyond the Basics: More Complex Percentage Problems
While calculating 15% of 25 is relatively straightforward, more complex percentage problems require a deeper understanding of the concepts involved. Here are a few examples:
-
Finding the Percentage Increase or Decrease: This involves calculating the percentage change between two values. For example, if the price of an item increases from $20 to $25, the percentage increase is calculated as: [(25-20)/20] * 100% = 25%.
-
Finding the Original Value: Sometimes, you know the percentage and the resulting value, and you need to find the original value. For example, if an item is on sale for $17.50 after a 15% discount, the original price can be calculated as: $17.50 / (1 - 0.15) = $20.59 (approximately).
-
Working with Multiple Percentages: Problems may involve applying multiple percentages sequentially or calculating the overall effect of combining several percentage changes. This often requires careful consideration of the order of operations and the compounding effect of multiple percentages.
Frequently Asked Questions (FAQs)
-
What is the easiest way to calculate percentages? Using a calculator is usually the quickest method. However, understanding the underlying principles (fraction, decimal, and proportion methods) helps you to solve problems even without a calculator and fosters a deeper comprehension of the concept.
-
How can I improve my skills in percentage calculations? Practice is key. Start with simple problems and gradually move towards more complex ones. Working through different types of problems and using various methods will strengthen your understanding and build your confidence.
-
Are there any online tools or calculators for percentage calculations? Yes, many websites and apps offer percentage calculators that can help with various percentage-related calculations. However, relying solely on calculators without understanding the concepts is not advisable.
-
Why are percentages important in everyday life? Percentages are used extensively in various aspects of life, including finance, shopping, statistics, and more. Understanding percentages empowers you to make informed decisions in numerous situations.
Conclusion: Mastering Percentages for a Brighter Future
This article has explored the concept of percentages in depth, providing a comprehensive understanding of how to calculate them and apply this knowledge to real-world problems. We've answered the initial question – 15% of 25 is 3.75 – but more importantly, we’ve equipped you with the skills to tackle various percentage-related challenges confidently. Mastering percentages is not just about solving mathematical problems; it's about developing a crucial life skill that empowers you to make informed decisions, analyze data effectively, and navigate the complexities of the modern world with greater ease and confidence. From budgeting and shopping to investing and understanding statistics, a firm grasp of percentages is an invaluable asset for everyone.
Latest Posts
Latest Posts
-
Gcf Of 25 And 45
Sep 11, 2025
-
11 50 As A Percent
Sep 11, 2025
-
X Cubed Times X Cubed
Sep 11, 2025
-
Gcf Of 5 And 4
Sep 11, 2025
-
Gcf Of 12 And 54
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Whats 15 Percent Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.