11 50 As A Percent
saludintensiva
Sep 11, 2025 · 5 min read
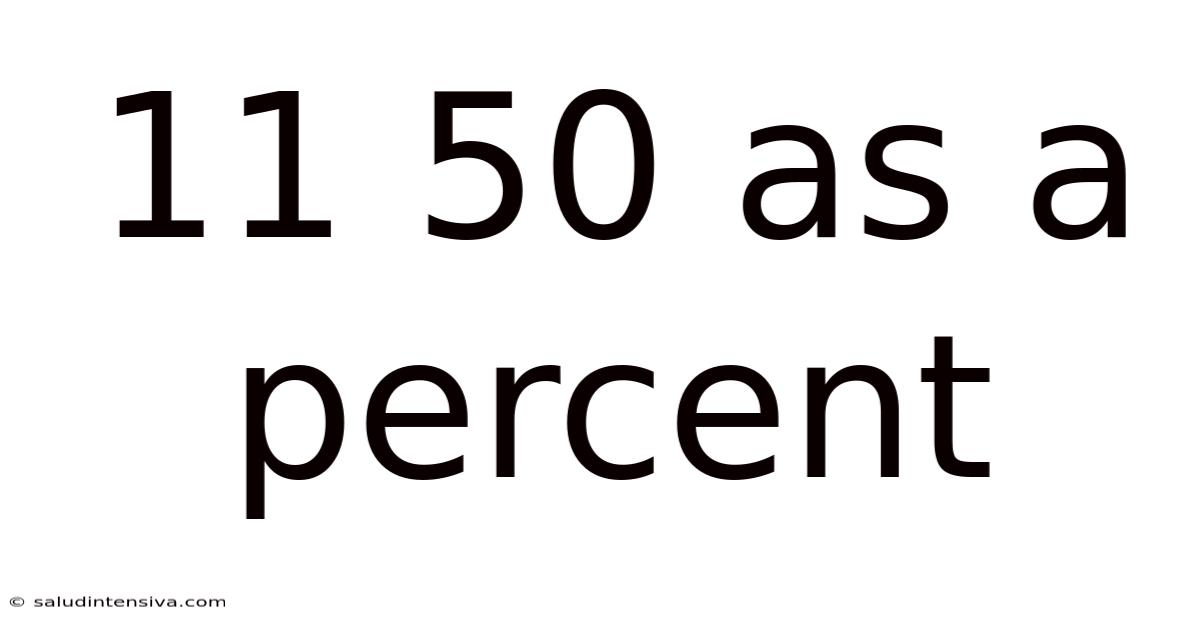
Table of Contents
Understanding 11/50 as a Percent: A Comprehensive Guide
Converting fractions to percentages is a fundamental skill in mathematics with applications spanning various fields, from finance and statistics to everyday calculations. This article delves into the process of converting the fraction 11/50 into a percentage, providing a detailed explanation suitable for learners of all levels. We'll explore the underlying concepts, demonstrate the calculation method, and offer practical examples to solidify your understanding. We'll also address common misconceptions and answer frequently asked questions to ensure a complete grasp of this topic.
Introduction: Fractions, Decimals, and Percentages – The Interconnected Trio
Before diving into the specific conversion of 11/50, let's establish a foundational understanding of the relationship between fractions, decimals, and percentages. These three represent different ways of expressing the same numerical value, making them interchangeable.
-
Fraction: A fraction represents a part of a whole, expressed as a ratio of two numbers – the numerator (top number) and the denominator (bottom number). For instance, 11/50 means 11 parts out of a total of 50 parts.
-
Decimal: A decimal represents a fraction where the denominator is a power of 10 (10, 100, 1000, etc.). Decimals use a decimal point to separate the whole number part from the fractional part.
-
Percentage: A percentage represents a fraction where the denominator is 100. It signifies "per hundred" and is denoted by the symbol %.
The ability to convert between these forms is crucial for solving various mathematical problems and interpreting data effectively.
Method 1: Converting the Fraction to a Decimal, Then to a Percentage
This method involves a two-step process: first converting the fraction to a decimal, and then converting the decimal to a percentage.
Step 1: Converting the Fraction to a Decimal
To convert a fraction to a decimal, we simply divide the numerator by the denominator. In this case:
11 ÷ 50 = 0.22
Step 2: Converting the Decimal to a Percentage
To convert a decimal to a percentage, we multiply the decimal by 100 and add the percent sign (%).
0.22 × 100 = 22%
Therefore, 11/50 is equal to 22%.
Method 2: Direct Conversion Using the Concept of "Per Hundred"
This method leverages the core definition of a percentage as a fraction with a denominator of 100. We need to find an equivalent fraction to 11/50 that has a denominator of 100.
To achieve this, we ask ourselves: "What number, when multiplied by 50, gives us 100?" The answer is 2.
Since we multiply the denominator by 2 to get 100, we must also multiply the numerator by 2 to maintain the same value:
(11 × 2) / (50 × 2) = 22/100
Since 22/100 means 22 parts out of 100, this directly translates to 22%.
Understanding the Concept: Proportions and Ratios
The conversion of fractions to percentages fundamentally involves understanding proportions and ratios. A percentage simply expresses a ratio as a fraction of 100. In the case of 11/50, we are essentially asking: "What is the equivalent ratio if we were to express it with a denominator of 100?" Solving this proportion leads us to the percentage value.
Practical Applications: Real-World Examples
The ability to convert fractions to percentages is invaluable in numerous real-world scenarios. Here are a few examples:
-
Calculating Discounts: If a store offers a 11/50 discount on an item, converting this fraction to 22% allows for easier calculation of the final price.
-
Analyzing Test Scores: If a student answers 11 out of 50 questions correctly on a test, their score is 22%, providing a clear understanding of their performance.
-
Financial Calculations: In finance, percentages are frequently used to represent interest rates, returns on investments, or changes in stock prices. Converting fractions to percentages helps in analyzing these financial data.
-
Statistical Analysis: In statistics, percentages are often used to represent proportions within a data set. Converting fractions to percentages simplifies the interpretation of data.
Common Misconceptions and Errors
While the conversion process is relatively straightforward, some common errors can arise:
-
Incorrect order of division: Remember to divide the numerator (11) by the denominator (50), not the other way around.
-
Forgetting to multiply by 100: A crucial step in converting a decimal to a percentage is multiplying by 100. Omitting this step will lead to an incorrect answer.
-
Misinterpreting the fraction: Ensure you correctly identify the numerator and the denominator of the fraction before beginning the calculation.
Frequently Asked Questions (FAQ)
Q1: Can I convert any fraction to a percentage?
Yes, any fraction can be converted to a percentage. The process involves dividing the numerator by the denominator and multiplying the result by 100.
Q2: What if the decimal has more than two decimal places after conversion?
If the resulting decimal has more than two decimal places, you can round it to the nearest hundredth for practical purposes. For instance, if the decimal is 0.225, you would round it to 0.23 and express it as 23%.
Q3: What if the denominator of the fraction is not a factor of 100?
Even if the denominator is not a factor of 100, you can still convert the fraction to a percentage using the method of dividing the numerator by the denominator and multiplying by 100.
Q4: Are there other ways to convert 11/50 to a percentage besides the methods described above?
While the methods described provide the most straightforward approaches, you could also use proportions or cross-multiplication techniques to solve for the equivalent percentage. However, the methods outlined are generally more efficient and easier to understand.
Conclusion: Mastering Fraction-to-Percentage Conversions
Converting 11/50 to a percentage, resulting in 22%, is a fundamental skill with widespread applications. Understanding the underlying principles of fractions, decimals, and percentages, and mastering the conversion methods, empowers you to confidently tackle similar problems in various contexts. By practicing these methods and addressing potential misconceptions, you'll develop a robust understanding of this crucial mathematical concept. Remember, consistent practice is key to mastering any mathematical skill, and this holds true for converting fractions to percentages as well. So, keep practicing, and you'll find these calculations become second nature!
Latest Posts
Latest Posts
-
1 9 As A Percent
Sep 11, 2025
-
Gcf Of 48 And 60
Sep 11, 2025
-
13 Percent In Decimal Form
Sep 11, 2025
-
9 7 9 As A Decimal
Sep 11, 2025
-
7 3 As A Decimal
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 11 50 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.