13 Percent In Decimal Form
saludintensiva
Sep 11, 2025 · 5 min read
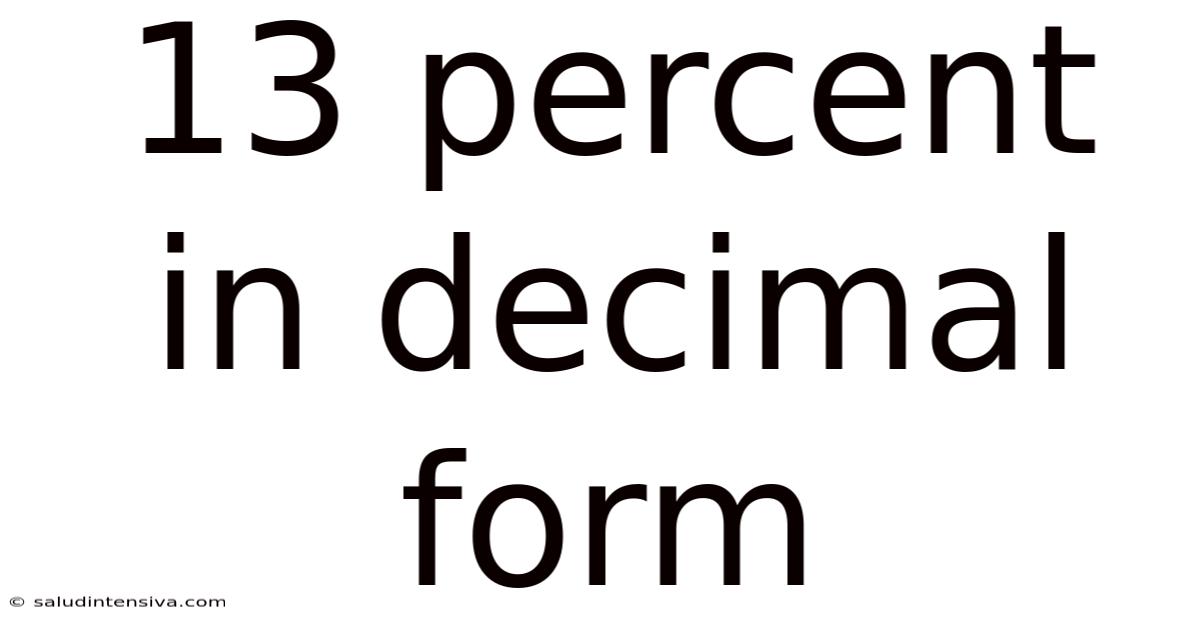
Table of Contents
13 Percent in Decimal Form: A Comprehensive Guide
Understanding percentages and their decimal equivalents is a fundamental skill in mathematics and numerous real-world applications. This article provides a comprehensive guide to converting 13 percent into its decimal form, explaining the underlying principles and offering practical examples to solidify your understanding. We'll delve into the process, explore related concepts, and answer frequently asked questions, ensuring you master this essential skill.
Introduction: Percentages and Decimals
Percentages and decimals are two different ways of representing parts of a whole. A percentage represents a fraction of 100, denoted by the symbol %. A decimal represents a fraction where the denominator is a power of 10. Converting between these forms is crucial for various calculations, including those involving discounts, taxes, interest rates, and statistical analysis. This article focuses specifically on understanding and calculating the decimal equivalent of 13%.
Converting 13% to Decimal Form: The Simple Method
The most straightforward way to convert a percentage to a decimal is to divide the percentage by 100. In this case, we have 13%. To convert 13% to a decimal, we simply perform the following calculation:
13% ÷ 100 = 0.13
Therefore, 13% in decimal form is 0.13. This is a fundamental conversion that applies to all percentages. To convert any percentage to its decimal equivalent, simply divide by 100.
Understanding the Underlying Principle
The conversion from percentage to decimal stems from the definition of a percentage. A percentage is a fraction out of 100. 13% means 13 out of 100, which can be written as the fraction 13/100. Dividing 13 by 100 gives us 0.13. This demonstrates the equivalence between the fraction, the percentage, and the decimal representation.
Practical Applications of Decimal Equivalents
The ability to convert percentages to decimals is essential in numerous real-world scenarios:
-
Calculating discounts: If a store offers a 13% discount on an item, you can easily calculate the discount amount by multiplying the item's price by 0.13.
-
Determining taxes: Similarly, if a sales tax is 13%, you can calculate the tax amount by multiplying the price by 0.13.
-
Financial calculations: Interest rates, loan calculations, and investment returns often involve percentages, requiring conversion to decimals for accurate calculations.
-
Statistical analysis: Many statistical measures, such as percentages, proportions, and probabilities, are often expressed in decimal form for computational ease.
-
Scientific calculations: In fields like chemistry and physics, concentrations, efficiencies, and other quantities are often expressed as percentages and frequently need conversion to decimal form for calculations and analysis.
Beyond 13%: Generalizing the Conversion Process
The process of converting percentages to decimals is consistent across all values. Let's look at some examples:
- 25%: 25% ÷ 100 = 0.25
- 5%: 5% ÷ 100 = 0.05
- 150%: 150% ÷ 100 = 1.5
- 0.5%: 0.5% ÷ 100 = 0.005
Notice that percentages greater than 100% result in decimal values greater than 1, while percentages less than 1% result in decimal values less than 0.01. The method remains the same: divide by 100.
Alternative Method: Moving the Decimal Point
A quicker method to convert a percentage to a decimal is to move the decimal point two places to the left. For example, in 13%, the decimal point is implicitly located after the 3 (13.0%). Moving the decimal point two places to the left gives us 0.13. This shortcut is derived from the division by 100, as dividing by 100 is equivalent to moving the decimal point two places to the left.
Converting Decimals Back to Percentages
The reverse process—converting a decimal to a percentage—is equally important. To do this, simply multiply the decimal by 100 and add the "%" symbol. For example, to convert 0.13 back to a percentage:
0.13 x 100 = 13%
This demonstrates the inverse relationship between percentages and decimals.
Working with Fractions and Percentages
Often, you'll need to work with fractions and percentages together. Remember that to convert a fraction to a percentage, you first convert the fraction to a decimal by dividing the numerator by the denominator, and then multiply by 100 and add the % symbol. For instance:
1/4 = 0.25 = 25%
1/2 = 0.5 = 50%
3/5 = 0.6 = 60%
Advanced Applications: Compound Interest and Exponential Growth
Understanding decimal equivalents of percentages is particularly crucial when dealing with compound interest and exponential growth. These concepts involve repeated multiplication using the decimal form of the percentage growth rate. For example, if you have an initial investment that grows at 13% annually, you'd use 0.13 in the compound interest formula to calculate the future value. Accurate calculations in finance heavily rely on this conversion.
Frequently Asked Questions (FAQ)
Q: What is the difference between 0.13 and 13%?
A: They represent the same value but in different forms. 0.13 is the decimal form, while 13% is the percentage form. They both represent 13 parts out of 100.
Q: Can I convert a percentage with a fraction, such as 13 1/2%, to a decimal?
A: Yes, first convert the mixed number to an improper fraction (27/2). Then convert the fraction to a decimal (27/2 = 13.5), and finally convert the decimal to a percentage (13.5/100 = 0.135).
Q: Why is it important to understand this conversion?
A: This conversion is fundamental for numerous calculations across various fields, ensuring accuracy and efficiency in mathematical and real-world applications. It’s a cornerstone of financial calculations, statistical analysis, and various scientific disciplines.
Q: Are there any online tools to help with percentage-decimal conversions?
A: While many online calculators exist, understanding the underlying principle of dividing by 100 or moving the decimal point two places is more valuable than relying solely on tools. This ensures you grasp the concept and can perform the conversion manually when needed.
Conclusion: Mastering Percentage-Decimal Conversions
Converting 13% to its decimal equivalent, 0.13, is a simple yet essential skill. This process, along with understanding the reverse conversion, is fundamental for navigating various mathematical and real-world situations. Mastering this conversion empowers you to confidently tackle calculations involving discounts, taxes, interest, statistical analysis, and many other applications. Remember the core principle: dividing a percentage by 100 (or moving the decimal point two places to the left) yields its decimal equivalent. By internalizing this straightforward method, you equip yourself with a powerful tool for problem-solving in numerous contexts.
Latest Posts
Latest Posts
-
600 M2 To Sq Ft
Sep 11, 2025
-
7 18 As A Decimal
Sep 11, 2025
-
Convert 81 F To Celsius
Sep 11, 2025
-
3 Square 4 Square
Sep 11, 2025
-
Half Of 5 1 4
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 13 Percent In Decimal Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.