7 18 As A Decimal
saludintensiva
Sep 11, 2025 · 5 min read
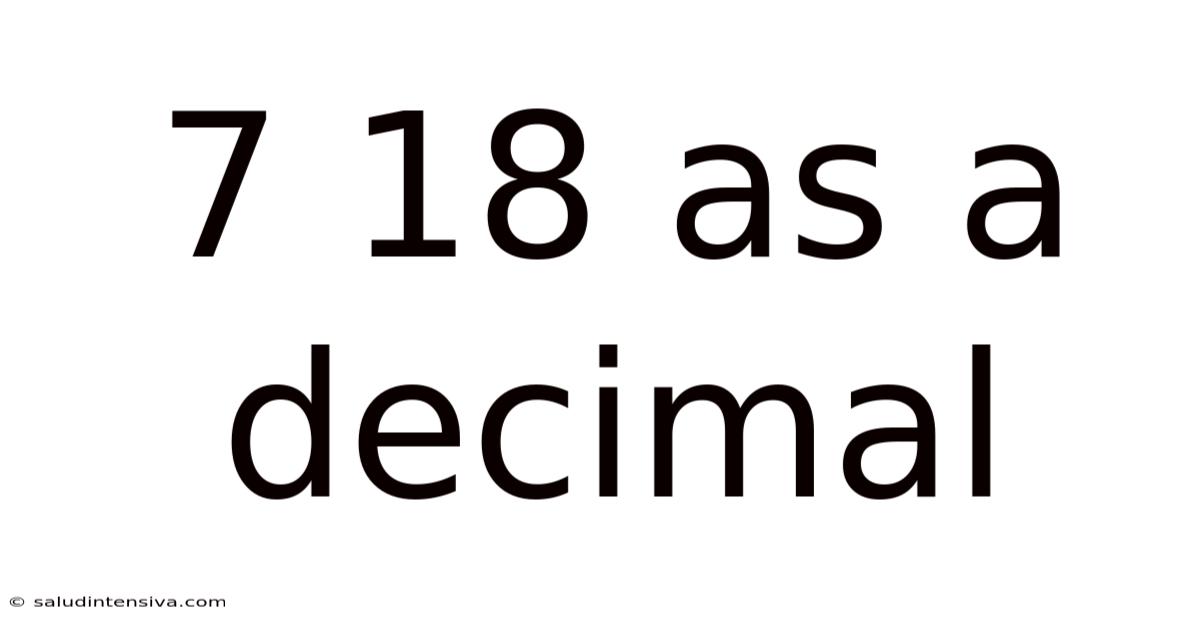
Table of Contents
7/18 as a Decimal: A Comprehensive Guide to Fraction-to-Decimal Conversion
Converting fractions to decimals is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced scientific computations. This comprehensive guide will delve into the process of converting the fraction 7/18 into its decimal equivalent, exploring different methods and providing a deeper understanding of the underlying mathematical principles. We'll also address common misconceptions and answer frequently asked questions. Understanding this conversion is key to mastering decimal representation and building a strong foundation in numeracy.
Understanding Fractions and Decimals
Before we embark on the conversion of 7/18, let's briefly revisit the concepts of fractions and decimals. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). A decimal is a number expressed in the base-10 system, using a decimal point to separate the whole number part from the fractional part. Converting a fraction to a decimal essentially means expressing the fractional part of the whole as a decimal representation.
Method 1: Long Division
The most straightforward method to convert a fraction to a decimal is through long division. We divide the numerator (7) by the denominator (18).
-
Set up the long division: Write 7 as the dividend (inside the division symbol) and 18 as the divisor (outside the division symbol). Add a decimal point and a zero to the dividend to begin the division process.
-
Perform the division: Since 18 doesn't go into 7, we add a zero to the dividend, making it 70. 18 goes into 70 three times (18 x 3 = 54). Write the '3' above the zero in the dividend. Subtract 54 from 70, resulting in 16.
-
Continue the process: Bring down another zero, making it 160. 18 goes into 160 eight times (18 x 8 = 144). Write the '8' above the second zero. Subtract 144 from 160, resulting in 16.
-
Repeating decimal: Notice a pattern? We're back to 16. This indicates a repeating decimal. We can continue the process, but the digits will repeat infinitely: 3, 8, 3, 8, and so on.
Therefore, 7/18 as a decimal is approximately 0.3888... or 0.3̅8. The bar over the '8' signifies that the digit 8 repeats infinitely.
Method 2: Converting to an Equivalent Fraction with a Denominator of 10, 100, 1000, etc.
This method involves finding an equivalent fraction with a denominator that is a power of 10 (10, 100, 1000, and so on). This is not always possible, especially with fractions like 7/18. However, let's explore this approach to understand its limitations.
To convert 7/18 to a decimal using this method, we would need to find a number that, when multiplied by 18, results in a power of 10. Unfortunately, 18 does not have such a convenient factor. This method is more effective with fractions that have denominators that are factors of powers of 10 (like 2, 5, 4, 25, 8, 125, etc.).
Method 3: Using a Calculator
The simplest way to convert 7/18 to a decimal is using a calculator. Simply divide 7 by 18. Most calculators will display the result as 0.388888... or a similar representation indicating the repeating decimal. While convenient, understanding the underlying process through long division is essential for a deeper grasp of the concept.
Understanding Repeating Decimals
The result of converting 7/18 to a decimal, 0.3̅8, is a repeating decimal. This means that the decimal representation has a sequence of digits that repeat infinitely. These repeating decimals are often represented with a bar over the repeating sequence. Understanding repeating decimals is crucial in various mathematical contexts.
Significance of Repeating Decimals
The occurrence of repeating decimals highlights the relationship between rational and irrational numbers. A rational number can be expressed as a fraction of two integers (like 7/18). Rational numbers either have a terminating decimal representation (e.g., 1/4 = 0.25) or a repeating decimal representation (e.g., 7/18 = 0.3̅8). An irrational number cannot be expressed as a fraction of two integers and has a non-repeating, non-terminating decimal representation (e.g., π).
Rounding Repeating Decimals
In practical applications, we often need to round repeating decimals to a certain number of decimal places. For example, we might round 0.3̅8 to 0.39 (rounded to two decimal places) or 0.389 (rounded to three decimal places). The method of rounding depends on the context and required precision.
Applications of Fraction-to-Decimal Conversion
The ability to convert fractions to decimals is crucial in many fields, including:
- Science and Engineering: Precise measurements and calculations often require decimal representations.
- Finance: Calculating interest rates, discounts, and other financial computations frequently involve decimal numbers.
- Everyday Life: Many situations, from cooking to calculating distances, involve fractions that are easily converted to decimals for easier computation.
Frequently Asked Questions (FAQ)
Q: Why does 7/18 result in a repeating decimal?
A: A fraction results in a repeating decimal when its denominator (in its simplest form) contains prime factors other than 2 and 5. The denominator 18 (which simplifies to 2 x 3²) contains the prime factor 3, leading to a repeating decimal.
Q: Can all fractions be expressed as terminating or repeating decimals?
A: Yes, all fractions (rational numbers) can be expressed as either terminating or repeating decimals.
Q: How do I round a repeating decimal correctly?
A: The standard rounding rules apply. If the digit after the desired place is 5 or greater, round up; otherwise, round down.
Q: Is there a way to predict if a fraction will result in a repeating decimal without performing the division?
A: Yes. Simplify the fraction to its lowest terms. If the denominator contains prime factors other than 2 and 5, the decimal representation will be repeating.
Conclusion
Converting 7/18 to a decimal, resulting in the repeating decimal 0.3̅8, demonstrates a fundamental concept in mathematics. This process, whether done through long division, using a calculator, or understanding the relationship between the fraction's denominator and the resulting decimal, reinforces the importance of understanding rational numbers and their decimal representations. This knowledge is essential for various applications across numerous fields, solidifying its importance in mathematical literacy. The ability to accurately convert fractions to decimals, understand repeating decimals, and apply appropriate rounding techniques are invaluable skills for anyone seeking a strong foundation in mathematics.
Latest Posts
Latest Posts
-
To The 2 3 Power
Sep 11, 2025
-
Calculate Interquartile Range In Excel
Sep 11, 2025
-
Is 2 5 Greater Than 1 3
Sep 11, 2025
-
Gcf Of 20 And 40
Sep 11, 2025
-
Lcm Of 9 And 3
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 7 18 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.