Is 2/5 Greater Than 1/3
saludintensiva
Sep 11, 2025 · 6 min read
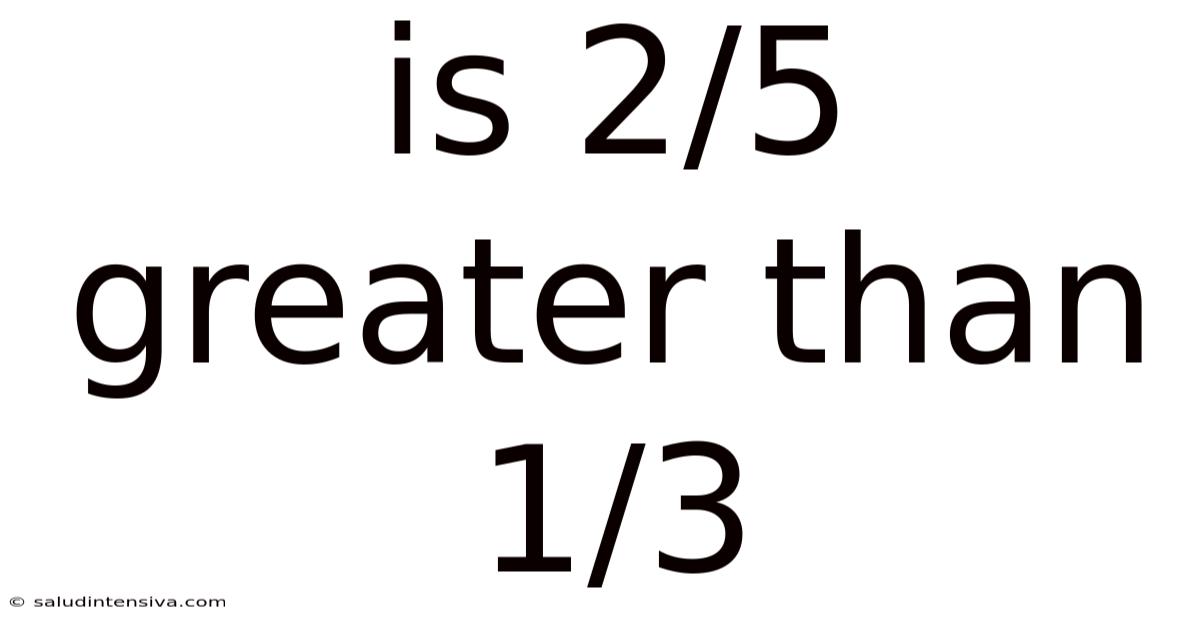
Table of Contents
Is 2/5 Greater Than 1/3? A Comprehensive Exploration of Fraction Comparison
Is 2/5 greater than 1/3? This seemingly simple question opens the door to a deeper understanding of fractions, a fundamental concept in mathematics with wide-ranging applications in everyday life. This article will not only answer this question definitively but will also equip you with the skills and knowledge to compare any two fractions with confidence. We'll explore various methods, delve into the underlying mathematical principles, and address common misconceptions. By the end, you'll be able to tackle fraction comparisons with ease and a newfound appreciation for their practical significance.
Understanding Fractions: A Quick Recap
Before diving into the comparison, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into. For example, in the fraction 2/5, the numerator is 2, and the denominator is 5, meaning we have 2 out of 5 equal parts.
Method 1: Finding a Common Denominator
The most straightforward method for comparing fractions is to find a common denominator. This involves finding a number that is a multiple of both denominators. Once we have a common denominator, we can directly compare the numerators.
Let's compare 2/5 and 1/3.
-
Find the least common multiple (LCM) of the denominators: The denominators are 5 and 3. The LCM of 5 and 3 is 15 (since 5 x 3 = 15).
-
Convert the fractions to equivalent fractions with the common denominator:
-
To convert 2/5 to an equivalent fraction with a denominator of 15, we multiply both the numerator and denominator by 3: (2 x 3) / (5 x 3) = 6/15.
-
To convert 1/3 to an equivalent fraction with a denominator of 15, we multiply both the numerator and denominator by 5: (1 x 5) / (3 x 5) = 5/15.
-
-
Compare the numerators: Now we compare 6/15 and 5/15. Since 6 > 5, we conclude that 6/15 > 5/15.
-
Therefore, 2/5 > 1/3.
Method 2: Converting to Decimals
Another effective method is to convert the fractions to decimals. This involves dividing the numerator by the denominator for each fraction.
-
Convert 2/5 to a decimal: 2 ÷ 5 = 0.4
-
Convert 1/3 to a decimal: 1 ÷ 3 ≈ 0.333... (this is a repeating decimal)
-
Compare the decimals: Since 0.4 > 0.333..., we can conclude that 2/5 > 1/3.
This method is particularly useful when dealing with fractions that are difficult to compare using a common denominator. However, remember that repeating decimals can sometimes require careful consideration of the precision you need.
Method 3: Visual Representation
Visualizing fractions can be incredibly helpful, especially for beginners. We can represent fractions using diagrams, such as circles or rectangles, divided into equal parts.
Imagine two identical circles. Divide the first circle into 5 equal parts and shade 2 of them (representing 2/5). Divide the second circle into 3 equal parts and shade 1 of them (representing 1/3). By visually comparing the shaded areas, it becomes clear that the shaded area in the first circle (2/5) is larger than the shaded area in the second circle (1/3).
This method provides a concrete, intuitive understanding of fraction comparison, making it easier to grasp the concept, especially for younger learners.
The Mathematical Reasoning Behind Fraction Comparison
The methods above all rely on the fundamental principle that fractions represent proportions. When we find a common denominator, we're essentially expressing both fractions in terms of the same unit of measurement, allowing for a direct comparison of their magnitudes. Similarly, converting to decimals allows for a direct numerical comparison. The visual representation reinforces this concept by showing the proportional sizes directly.
The core mathematical concept is the idea of equivalence. When we multiply the numerator and denominator of a fraction by the same number (other than zero), we are creating an equivalent fraction that represents the same proportion. This is crucial for finding common denominators and ensuring accurate comparisons.
Addressing Common Misconceptions
A common misconception is that simply comparing numerators or denominators independently is sufficient. This is incorrect. For example, some might mistakenly think that 1/3 is larger than 2/5 because 3 > 2 (comparing denominators). However, this ignores the fact that the denominators represent different sized parts of the whole.
Another potential misunderstanding is the belief that larger numbers always imply a larger fraction. While this might be true in some cases (like comparing 2/5 and 3/5), it is not universally applicable. The relationship between the numerator and denominator is what ultimately determines the size of the fraction.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to compare fractions? A: Yes, you can use a calculator to convert fractions to decimals, which allows for a direct comparison. However, understanding the underlying methods of finding a common denominator or visual representation is crucial for developing a deeper understanding of fractions.
-
Q: What if the fractions have very large denominators? A: Finding a common denominator might become computationally intensive with very large numbers. In such cases, converting to decimals is often a more efficient approach.
-
Q: Are there other methods to compare fractions? A: While the methods described above are the most common and practical, more advanced techniques exist, such as cross-multiplication, that are useful in certain situations.
-
Q: Why is understanding fraction comparison important? A: Fraction comparison is essential for many aspects of mathematics and real-world applications. From baking (measuring ingredients) to calculating probabilities to understanding financial ratios, the ability to compare fractions is a fundamental skill.
Conclusion: Mastering Fraction Comparison
Determining whether 2/5 is greater than 1/3 is more than just a simple mathematical exercise. It's an opportunity to delve into the fundamentals of fractions and develop a strong understanding of their properties. By mastering the methods of finding common denominators, converting to decimals, and utilizing visual representations, you can confidently compare any two fractions and apply this skill to numerous situations in your life and studies. Remember, the key is not just to get the right answer but to understand why that answer is correct, solidifying your mathematical foundation and building confidence in your abilities. Through practice and a deeper understanding of the underlying concepts, fraction comparison will cease to be a challenge and become a tool that empowers you to tackle more complex mathematical problems with ease.
Latest Posts
Latest Posts
-
Add To Multiply To Calculator
Sep 11, 2025
-
Lcm Of 9 12 15
Sep 11, 2025
-
Lcm Of 8 And 24
Sep 11, 2025
-
2 3 X 1 12
Sep 11, 2025
-
2 3 7 As A Decimal
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Is 2/5 Greater Than 1/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.