Lcm Of 9 12 15
saludintensiva
Sep 11, 2025 · 6 min read
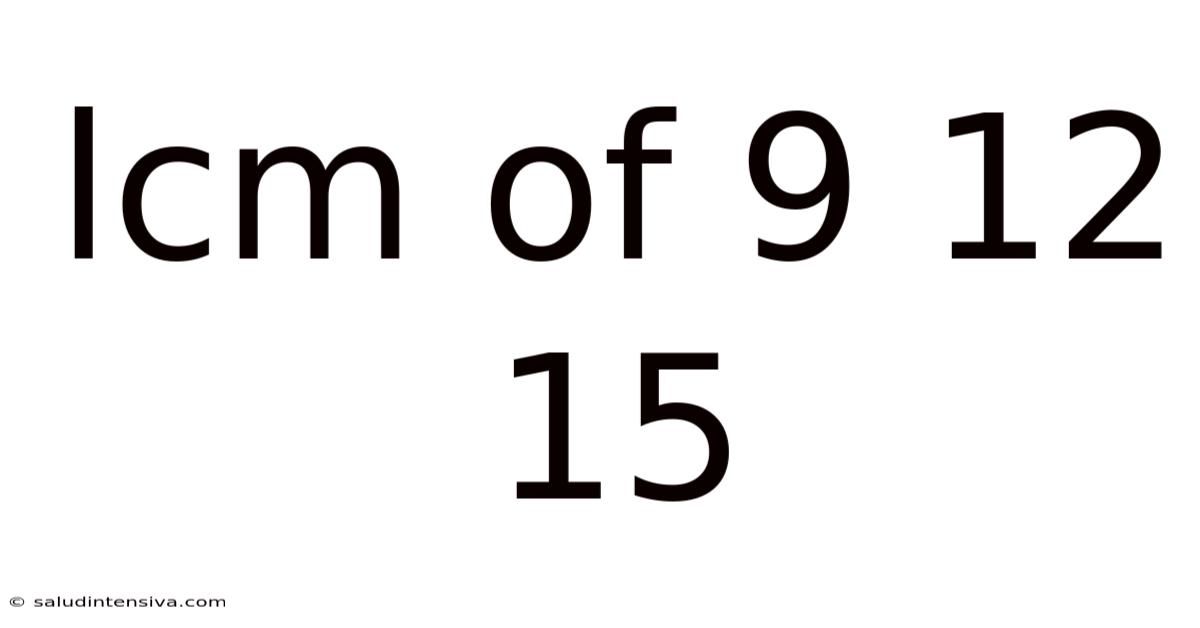
Table of Contents
Finding the Least Common Multiple (LCM) of 9, 12, and 15: A Comprehensive Guide
Finding the least common multiple (LCM) of a set of numbers is a fundamental concept in mathematics with applications ranging from simple fraction addition to complex scheduling problems. This comprehensive guide will walk you through various methods to calculate the LCM of 9, 12, and 15, explain the underlying mathematical principles, and answer frequently asked questions. Understanding LCM is crucial for various mathematical operations and real-world scenarios, making this a valuable skill to master.
Introduction: What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers without leaving a remainder. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. For example, the LCM of 2 and 3 is 6 because 6 is the smallest number that is divisible by both 2 and 3. This concept extends to more than two numbers, as we'll see with our example of 9, 12, and 15.
Method 1: Listing Multiples
This is the most straightforward method, especially for smaller numbers. We list the multiples of each number until we find the smallest multiple common to all three.
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, 108, 117, 126, 135...
- Multiples of 12: 12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132, 144, 156, 168, 180...
- Multiples of 15: 15, 30, 45, 60, 75, 90, 105, 120, 135, 150, 165, 180, 195, 210, 225...
By comparing the lists, we can see that the smallest number common to all three lists is 180. Therefore, the LCM of 9, 12, and 15 is 180.
While this method is simple for smaller numbers, it becomes less efficient and more prone to error as the numbers get larger. Let's explore more efficient methods.
Method 2: Prime Factorization
This method is more efficient and systematic, especially for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM from those prime factors.
-
Find the prime factorization of each number:
- 9 = 3 x 3 = 3²
- 12 = 2 x 2 x 3 = 2² x 3
- 15 = 3 x 5
-
Identify the highest power of each prime factor present:
- The prime factors are 2, 3, and 5.
- The highest power of 2 is 2² = 4.
- The highest power of 3 is 3² = 9.
- The highest power of 5 is 5¹ = 5.
-
Multiply the highest powers together:
LCM(9, 12, 15) = 2² x 3² x 5 = 4 x 9 x 5 = 180
This method provides a more structured and reliable way to find the LCM, especially when dealing with larger numbers or a greater number of integers.
Method 3: Using the Greatest Common Divisor (GCD)
The LCM and GCD (Greatest Common Divisor) are closely related. There's a formula that connects them:
LCM(a, b, c) = (a x b x c) / GCD(a, b, c)
However, this formula is only directly applicable for two numbers. For more than two numbers, we need a more nuanced approach. We can use the GCD iteratively.
First, let's find the GCD of two of the numbers, say 9 and 12. We can use the Euclidean algorithm:
- 12 = 1 x 9 + 3
- 9 = 3 x 3 + 0
The GCD(9, 12) = 3.
Now, find the GCD of this result (3) and the remaining number (15):
- 15 = 5 x 3 + 0
The GCD(3, 15) = 3. This is the GCD of 9, 12, and 15.
Now, use the formula (but note this is simplified for explanation. A true iterative method is needed for larger sets): Instead of using the formula directly across all three numbers, we use it in a stepwise manner to find the LCM.
We have: LCM(9,12) = (9 * 12) / GCD(9,12) = (9 * 12) / 3 = 36. Then, LCM(36, 15) = (36 * 15) / GCD(36,15) = (36 * 15) / 3 = 180.
Therefore, the LCM(9, 12, 15) = 180. This method demonstrates the relationship between LCM and GCD. For more than two numbers, a more rigorous iterative approach applying the GCD calculation sequentially is required for accuracy.
Explanation of the Mathematical Principles
The success of the prime factorization method hinges on the Fundamental Theorem of Arithmetic, which states that every integer greater than 1 can be represented uniquely as a product of prime numbers (ignoring the order of the factors). This uniqueness allows us to systematically construct the LCM by taking the highest power of each prime factor present in the numbers.
The relationship between LCM and GCD is based on the property that the product of two integers is equal to the product of their LCM and GCD. While the formula directly applies for two numbers, for three or more, an iterative application of the GCD and LCM calculations is required to ensure accuracy.
Real-world Applications of LCM
The concept of LCM isn't just an abstract mathematical exercise. It finds practical applications in various real-world scenarios:
- Scheduling: Imagine three buses arrive at a bus stop at intervals of 9, 12, and 15 minutes. The LCM (180 minutes, or 3 hours) tells you when all three buses will arrive simultaneously again.
- Fraction Addition/Subtraction: Finding a common denominator when adding or subtracting fractions involves finding the LCM of the denominators.
- Project Management: If different tasks in a project take 9, 12, and 15 days to complete, the LCM helps determine the shortest time for all tasks to be completed simultaneously.
- Gear Ratios: In mechanical engineering, the LCM can be used to calculate gear ratios to synchronize the rotation of multiple gears.
Frequently Asked Questions (FAQ)
-
Q: What if the numbers have no common factors?
- A: If the numbers are relatively prime (meaning they share no common factors other than 1), their LCM is simply the product of the numbers.
-
Q: Can I use a calculator to find the LCM?
- A: Many scientific calculators have built-in functions to calculate the LCM of multiple numbers.
-
Q: Is there a formula for finding the LCM of more than two numbers?
- A: While there isn't a single, direct formula like the GCD formula, the prime factorization method and iterative GCD approaches are efficient and reliable methods for finding the LCM of any number of integers.
-
Q: Why is the LCM important in fractions?
- A: Finding a common denominator (which is the LCM of the denominators) is essential for adding or subtracting fractions, allowing us to combine them into a single fraction.
Conclusion
Finding the least common multiple (LCM) is a crucial skill in mathematics with practical applications in various fields. While the simple method of listing multiples works for smaller numbers, the prime factorization method provides a more efficient and reliable approach for larger numbers and a greater number of integers. Understanding the relationship between LCM and GCD further enhances your mathematical problem-solving abilities. Mastering the LCM calculation helps build a strong foundation in number theory and expands your problem-solving toolkit. Remember to choose the method best suited to the problem at hand; the prime factorization is generally the most efficient and reliable for larger numbers or more complex scenarios. The journey to understanding LCM is not merely about calculating numbers; it's about comprehending the fundamental principles that underpin various mathematical operations and their applications in the real world.
Latest Posts
Latest Posts
-
29 Billion As A Number
Sep 11, 2025
-
15 8 As A Mixed Number
Sep 11, 2025
-
How Long Is 117 Minutes
Sep 11, 2025
-
Lcm Of 28 And 16
Sep 11, 2025
-
What Is 10 Of 25 00
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 9 12 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.