What Is 10 Of 25.00
saludintensiva
Sep 11, 2025 · 5 min read
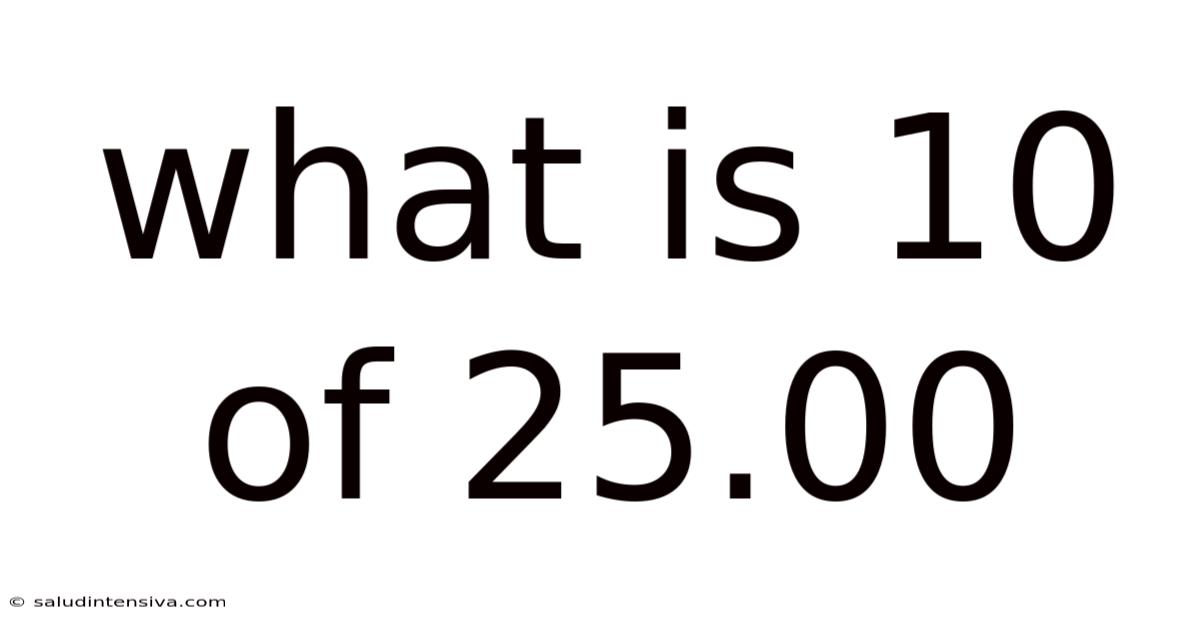
Table of Contents
What is 10% of 25.00? A Deep Dive into Percentages and Their Applications
Understanding percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and taxes to analyzing financial data and understanding statistical information. This article explores the seemingly simple question, "What is 10% of 25.00?", but it goes beyond a simple answer, delving into the underlying concepts, different methods of calculation, and the broader implications of percentage calculations.
Introduction: Deconstructing the Problem
The question, "What is 10% of 25.00?", asks us to find 10% of a given amount, 25.00. This involves understanding the meaning of percentage and applying the appropriate mathematical operations. A percentage represents a fraction of 100. For instance, 10% means 10 out of 100, or 10/100, which simplifies to 1/10. Therefore, finding 10% of 25.00 is equivalent to finding one-tenth of 25.00.
Methods for Calculating 10% of 25.00
There are several ways to calculate 10% of 25.00. Let's explore three common approaches:
1. The Direct Method (Using Fractions):
As mentioned earlier, 10% is equivalent to 1/10. Therefore, to find 10% of 25.00, we can simply multiply 25.00 by 1/10:
25.00 x (1/10) = 2.50
This method is straightforward and easy to understand, especially for those comfortable working with fractions.
2. The Decimal Method:
Percentages can also be expressed as decimals. 10% is equivalent to 0.10 (or simply 0.1). Therefore, we can calculate 10% of 25.00 by multiplying 25.00 by 0.1:
25.00 x 0.1 = 2.50
This method is particularly useful when using calculators, as it avoids the need to convert fractions.
3. The Proportion Method:
This method uses the concept of ratios and proportions. We can set up a proportion to solve the problem:
10/100 = x/25.00
Where 'x' represents the unknown value (10% of 25.00). To solve for 'x', we can cross-multiply:
10 * 25.00 = 100 * x
250 = 100x
x = 250/100 = 2.50
While slightly more complex, this method reinforces the underlying relationship between percentages, fractions, and ratios.
Therefore, 10% of 25.00 is 2.50.
Expanding the Concept: Beyond the Basic Calculation
While the calculation itself is simple, understanding the concept of percentages has far-reaching implications. Let's explore some practical applications:
-
Retail Discounts: Imagine a shirt priced at $25.00 is on sale with a 10% discount. The discount amount is 10% of $25.00, which we've calculated to be $2.50. The final price would be $25.00 - $2.50 = $22.50.
-
Sales Tax: If a sales tax rate is 10%, then the tax on a $25.00 item would be $2.50. The total cost, including tax, would be $25.00 + $2.50 = $27.50.
-
Financial Analysis: Percentages are crucial in financial statements. Profit margins, return on investment (ROI), and growth rates are all expressed as percentages. Understanding percentage calculations is essential for interpreting financial data and making informed decisions.
-
Statistical Analysis: Percentages are frequently used in statistical analysis to represent proportions and probabilities. For example, a survey might report that 10% of respondents prefer a certain product.
-
Scientific Applications: Percentages play a role in many scientific disciplines, such as chemistry (concentration of solutions) and biology (growth rates of populations).
Practical Applications: Real-World Scenarios
Let's explore some more complex scenarios involving percentage calculations:
Scenario 1: Calculating Multiple Percentages:
Suppose a store offers a 10% discount followed by an additional 5% discount for members. What would be the final price of a $25.00 item?
-
Step 1: Calculate the 10% discount: 25.00 x 0.10 = $2.50. The price after the first discount is $25.00 - $2.50 = $22.50.
-
Step 2: Calculate the 5% discount on the reduced price: $22.50 x 0.05 = $1.125.
-
Step 3: The final price is $22.50 - $1.125 = $21.375 (approximately $21.38).
Note: It is important to calculate discounts sequentially, not cumulatively (15% of the original price).
Scenario 2: Finding the Original Price:
Suppose an item is sold for $22.50 after a 10% discount. What was the original price?
This requires working backward. Let's represent the original price as 'x'. After a 10% discount, the remaining price is 90% (100% - 10%) of the original price. We can set up an equation:
0.90x = 22.50
x = 22.50 / 0.90 = 25.00
Therefore, the original price was $25.00.
Scenario 3: Calculating Percentage Increase or Decrease:
Let's say the price of an item increases from $20.00 to $25.00. What is the percentage increase?
-
Step 1: Calculate the difference: $25.00 - $20.00 = $5.00
-
Step 2: Divide the difference by the original price: $5.00 / $20.00 = 0.25
-
Step 3: Multiply by 100 to express as a percentage: 0.25 x 100 = 25%
Therefore, the price increased by 25%.
Frequently Asked Questions (FAQ)
- Q: What if I need to calculate a percentage other than 10%?
A: The same principles apply. Simply replace 0.1 (or 1/10) with the decimal or fractional equivalent of the desired percentage. For example, to calculate 25% of 25.00, you would multiply 25.00 by 0.25.
- Q: How can I calculate percentages without a calculator?
A: For simple percentages like 10%, 25%, or 50%, you can use mental math and fractional equivalents. For more complex percentages, you might need to resort to long multiplication or division.
- Q: Are there any online tools to help with percentage calculations?
A: Yes, many websites and apps provide percentage calculators. These tools can be helpful for quick calculations or for verifying your own calculations.
Conclusion: Mastering Percentages – A Lifelong Skill
Understanding percentages is not just about solving mathematical problems; it's about developing a crucial life skill. From managing personal finances to interpreting data and making informed decisions, the ability to calculate and interpret percentages is invaluable. While the basic calculation of "What is 10% of 25.00?" might seem straightforward, this article has explored the underlying concepts, provided alternative calculation methods, and demonstrated the practical applications of percentages in diverse real-world scenarios. By grasping these concepts, you'll be well-equipped to tackle more complex percentage problems and confidently apply this essential mathematical skill in your daily life. Remember to practice regularly to solidify your understanding and build your confidence in tackling percentage-related challenges.
Latest Posts
Latest Posts
-
Multiplication Of Square Roots Calculator
Sep 11, 2025
-
Conversao Fahrenheit Em Graus Celsius
Sep 11, 2025
-
Lcm Of 6 And 15
Sep 11, 2025
-
97 4 Degrees Fahrenheit To Celsius
Sep 11, 2025
-
27 8 As A Mixed Number
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about What Is 10 Of 25.00 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.