Lcm Of 9 And 3
saludintensiva
Sep 11, 2025 · 6 min read
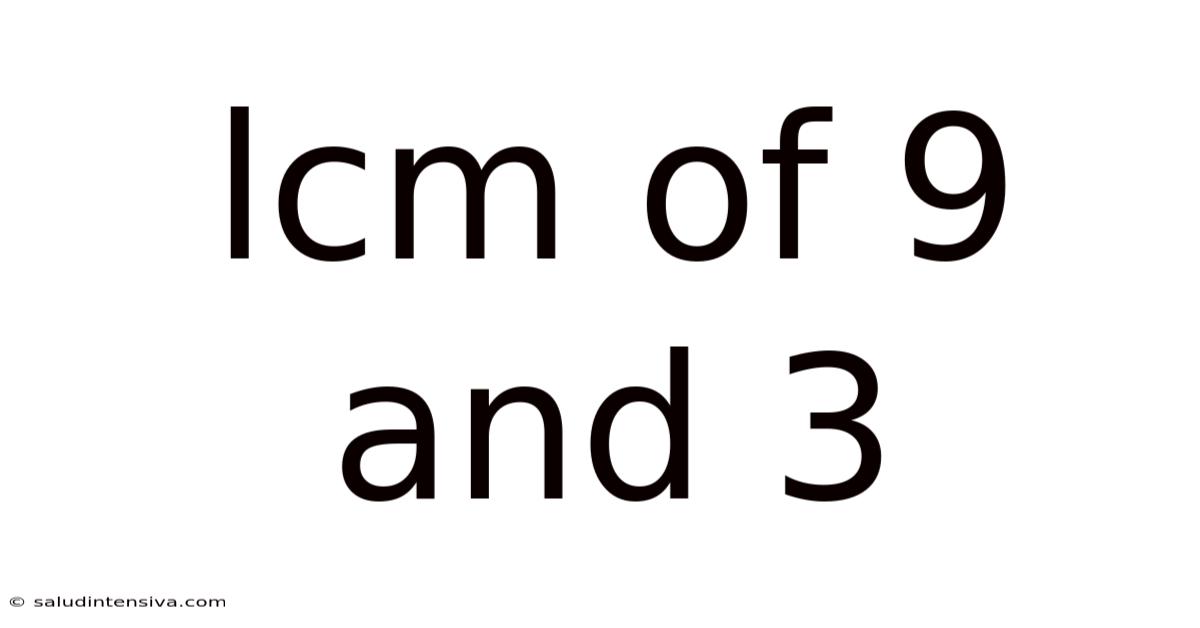
Table of Contents
Finding the Least Common Multiple (LCM) of 9 and 3: A Comprehensive Guide
Finding the least common multiple (LCM) is a fundamental concept in mathematics, particularly important in areas like fractions, algebra, and even music theory. This article provides a comprehensive explanation of how to find the LCM of 9 and 3, exploring different methods and delving into the underlying mathematical principles. Understanding LCMs is crucial for various mathematical operations, and this guide will equip you with the knowledge and skills to confidently tackle similar problems. We'll move beyond simply finding the answer and explore the 'why' behind the methods, making the concept clear and intuitive.
Understanding Least Common Multiples (LCMs)
Before we dive into calculating the LCM of 9 and 3, let's establish a clear understanding of what an LCM actually is. The least common multiple of two or more numbers is the smallest positive integer that is a multiple of all the numbers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly without leaving a remainder. For instance, if we consider the numbers 2 and 3, their multiples are:
- Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30...
The common multiples of 2 and 3 are 6, 12, 18, 24, and so on. The smallest of these common multiples is 6, therefore, the LCM of 2 and 3 is 6.
Method 1: Listing Multiples
The simplest method for finding the LCM, especially for smaller numbers like 9 and 3, is by listing the multiples of each number until you find the smallest common multiple.
Let's list the multiples of 9 and 3:
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90...
- Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27, 30...
By comparing the lists, we can see that the smallest number that appears in both lists is 9. Therefore, the LCM of 9 and 3 is 9.
Method 2: Prime Factorization
The prime factorization method is a more robust method that works well for larger numbers and allows for a systematic approach. This method involves breaking down each number into its prime factors. Prime factors are prime numbers (numbers divisible only by 1 and themselves) that multiply together to give the original number.
Let's find the prime factorization of 9 and 3:
- Prime factorization of 9: 3 x 3 = 3²
- Prime factorization of 3: 3
Now, we identify the highest power of each prime factor present in either factorization. In this case, the only prime factor is 3, and the highest power is 3¹. Therefore, the LCM is 3² = 9.
Method 3: Greatest Common Divisor (GCD) Method
The LCM and the greatest common divisor (GCD) are closely related. The GCD is the largest number that divides both numbers without leaving a remainder. There's a useful formula connecting the LCM and GCD:
LCM(a, b) * GCD(a, b) = a * b
First, let's find the GCD of 9 and 3 using the Euclidean algorithm:
- Divide the larger number (9) by the smaller number (3): 9 ÷ 3 = 3 with a remainder of 0.
- Since the remainder is 0, the GCD is the smaller number, which is 3.
Now, we can use the formula:
LCM(9, 3) * GCD(9, 3) = 9 * 3 LCM(9, 3) * 3 = 27 LCM(9, 3) = 27 ÷ 3 = 9
Why is the LCM Important?
Understanding LCMs is crucial for various mathematical operations and applications. Here are some key reasons:
-
Adding and Subtracting Fractions: Finding the LCM of the denominators is essential when adding or subtracting fractions with different denominators. You need to find a common denominator to perform the operation, and the LCM provides the smallest and most efficient common denominator.
-
Solving Problems Involving Cycles: LCMs are used to solve problems involving repeating cycles or events that occur at different intervals. For example, if two buses arrive at a stop every 9 minutes and 3 minutes respectively, the LCM will tell you when both buses will arrive simultaneously.
-
Simplifying Algebraic Expressions: LCMs are frequently used in simplifying algebraic fractions and expressions. Finding a common denominator allows for combining or simplifying terms.
-
Applications in Music Theory: LCMs are used in music theory to find the least common multiple of different rhythmic patterns, helping musicians synchronize complex musical passages.
A Deeper Dive into the Mathematics
The prime factorization method offers a deeper understanding of the mathematical principles behind LCM calculations. By breaking down numbers into their prime factors, we are essentially identifying the fundamental building blocks of those numbers. The LCM, obtained by taking the highest power of each prime factor, represents the smallest number that contains all the prime factors of both numbers in their entirety. This ensures that the LCM is divisible by both original numbers.
Frequently Asked Questions (FAQ)
Q1: Is the LCM always larger than both numbers?
A1: No. In cases where one number is a multiple of the other, as in the case of 9 and 3 (where 9 is a multiple of 3), the LCM is the larger of the two numbers.
Q2: What if I have more than two numbers?
A2: The process is similar. You can use the prime factorization method or iterative pairwise LCM calculations. For instance, to find the LCM of 3, 6, and 9, you would first find the LCM of 3 and 6, and then find the LCM of the result and 9.
Q3: Are there any shortcuts for finding the LCM?
A3: If one number is a factor of the other, the LCM is simply the larger number. For relatively small numbers, the listing multiples method can be quite quick. For larger numbers, prime factorization is a more efficient and reliable method.
Q4: How does the GCD method relate to the prime factorization method?
A4: Both methods are fundamentally linked. The GCD, found through prime factorization, reveals the common prime factors, and the LCM is built upon the remaining prime factors to create the smallest number divisible by both originals. The formula relating LCM and GCD elegantly highlights this connection.
Conclusion
Finding the least common multiple of 9 and 3, which is 9, demonstrates a fundamental concept in mathematics with broad applications. We explored three different methods – listing multiples, prime factorization, and using the GCD – highlighting their strengths and demonstrating how they lead to the same result. This article aimed not only to provide a solution but also to provide a solid understanding of the underlying mathematical principles and the practical significance of LCMs in various fields. By grasping these concepts, you will be better equipped to tackle more complex mathematical problems and appreciate the interconnectedness of different mathematical ideas. Remember, understanding the 'why' behind the mathematical operations is just as crucial as knowing the 'how'.
Latest Posts
Latest Posts
-
Add To Multiply To Calculator
Sep 11, 2025
-
Lcm Of 9 12 15
Sep 11, 2025
-
Lcm Of 8 And 24
Sep 11, 2025
-
2 3 X 1 12
Sep 11, 2025
-
2 3 7 As A Decimal
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 9 And 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.