3 Square + 4 Square
saludintensiva
Sep 11, 2025 · 7 min read
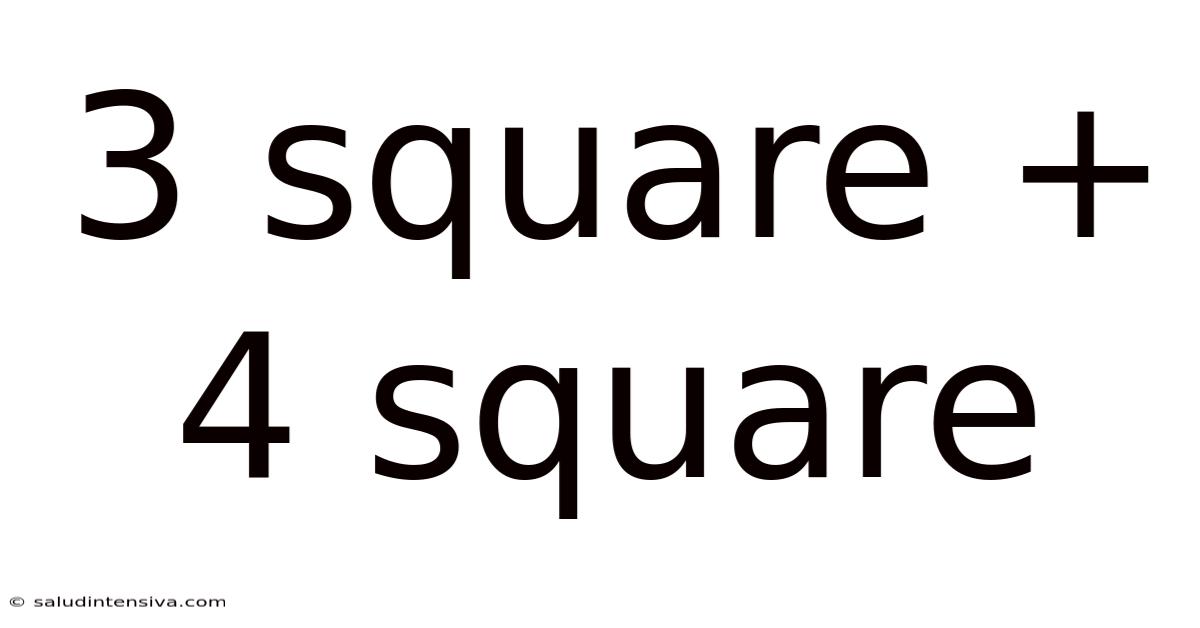
Table of Contents
Exploring the Pythagorean Puzzle: A Deep Dive into 3² + 4²
The simple equation 3² + 4² = 25 is more than just a basic arithmetic problem; it's a foundational element of geometry, trigonometry, and even advanced mathematical concepts. This seemingly straightforward calculation unlocks a world of understanding about right-angled triangles, the Pythagorean theorem, and the elegance of mathematical relationships. This article will explore this equation in depth, examining its implications, applications, and relevance across various mathematical fields. We'll move beyond the simple answer to uncover the deeper mathematical beauty hidden within.
Understanding the Basics: Squares and the Pythagorean Theorem
Before diving into the intricacies of 3² + 4², let's solidify our understanding of the fundamental concepts involved. The notation "3²" (read as "three squared") signifies 3 multiplied by itself: 3 x 3 = 9. Similarly, 4² is 4 x 4 = 16. Therefore, the equation 3² + 4² represents the sum of these squares: 9 + 16 = 25.
This seemingly simple calculation is intimately connected to the Pythagorean theorem, a cornerstone of geometry. The theorem states that in a right-angled triangle (a triangle with one 90-degree angle), the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides (called legs or cathetus). This relationship is expressed as:
a² + b² = c²
where 'a' and 'b' are the lengths of the legs, and 'c' is the length of the hypotenuse.
Our equation, 3² + 4² = 25, perfectly illustrates the Pythagorean theorem. If we consider a right-angled triangle with legs of length 3 and 4, the hypotenuse will have a length of √25 = 5. This classic 3-4-5 triangle is a fundamental example used in countless geometry problems and practical applications.
Applications of the 3-4-5 Triangle and its Significance
The 3-4-5 triangle, representing the solution to 3² + 4² = 5², holds immense significance across various fields:
-
Construction and Engineering: The 3-4-5 triangle is frequently used in construction to ensure right angles. By measuring 3 units along one side, 4 units along the other, and checking for a 5-unit distance between those points, builders can verify that the corner is perfectly square. This ensures accurate building foundations and structures.
-
Surveying and Mapping: Surveyors utilize the Pythagorean theorem and the 3-4-5 triangle to determine distances and angles accurately. This is crucial for land surveying, creating maps, and constructing infrastructure.
-
Navigation: Navigation systems and GPS technology rely on precise calculations involving distances and angles. The Pythagorean theorem plays a critical role in these calculations, enabling accurate positioning and route planning.
-
Computer Graphics and Game Development: In computer graphics and game development, the Pythagorean theorem is used extensively to calculate distances between points in two or three-dimensional space. This is fundamental for rendering realistic images and creating smooth game animations.
-
Physics and Engineering: Many physics and engineering problems involve calculations of distances, velocities, and forces. The Pythagorean theorem is an essential tool in solving these problems, particularly in problems involving vectors and their components.
Beyond the 3-4-5 Triangle: Generalizing the Pythagorean Theorem
While the 3-4-5 triangle is a prime example, the Pythagorean theorem applies to all right-angled triangles. The equation a² + b² = c² remains true regardless of the lengths of the legs. For instance:
-
A triangle with legs of 5 and 12: 5² + 12² = 25 + 144 = 169, and √169 = 13, so this is a 5-12-13 right-angled triangle.
-
A triangle with legs of 6 and 8: 6² + 8² = 36 + 64 = 100, and √100 = 10, giving us a 6-8-10 triangle (which is simply a scaled-up version of the 3-4-5 triangle).
These examples demonstrate that the Pythagorean theorem is a general principle, not limited to specific values. The relationship between the squares of the sides remains consistent for all right-angled triangles.
Proof of the Pythagorean Theorem: A Visual Demonstration
Numerous proofs of the Pythagorean theorem exist, demonstrating its mathematical rigor. One visually intuitive proof involves using geometric manipulation:
Imagine two squares, each with side length (a + b). Within each square, draw four identical right-angled triangles with legs 'a' and 'b', and hypotenuse 'c'.
In the first square, arrange the triangles so they leave a central square with side length 'c'. The area of this central square is c². The total area of the larger square is (a + b)².
In the second square, arrange the triangles differently, so they leave two smaller squares, one with side 'a' and the other with side 'b'. The areas of these smaller squares are a² and b², respectively. The total area of the larger square remains (a + b)².
Since both larger squares have the same area, we can equate the sum of the areas within:
a² + b² + 2(½ab) = c² + 2(½ab)
The terms 2(½ab) cancel out on both sides, leaving the Pythagorean theorem:
a² + b² = c²
This visual proof elegantly demonstrates the mathematical truth behind the Pythagorean theorem.
Exploring the Equation in Higher Dimensions: Beyond Two Dimensions
The Pythagorean theorem's principles extend beyond two dimensions. In three dimensions, the distance between two points (x₁, y₁, z₁) and (x₂, y₂, z₂) can be calculated using a three-dimensional version of the theorem:
d² = (x₂ - x₁)² + (y₂ - y₁)² + (z₂ - z₁)²
This formula finds applications in various fields, including:
- Physics: Calculating distances and displacements in three-dimensional space.
- Computer Graphics: Rendering three-dimensional objects and simulating movement.
- Navigation: Determining precise locations using three-dimensional coordinate systems.
Solving Problems Using the Pythagorean Theorem: Practical Examples
Let's solidify our understanding by applying the Pythagorean theorem to some practical examples:
Example 1: A ladder leans against a wall. The base of the ladder is 6 meters from the wall, and the top of the ladder reaches 8 meters up the wall. What is the length of the ladder?
Using the Pythagorean theorem:
a² + b² = c²
6² + 8² = c²
36 + 64 = c²
100 = c²
c = √100 = 10 meters
Therefore, the length of the ladder is 10 meters.
Example 2: A ship sails 15 km east and then 20 km north. How far is the ship from its starting point?
Again, using the Pythagorean theorem:
a² + b² = c²
15² + 20² = c²
225 + 400 = c²
625 = c²
c = √625 = 25 km
The ship is 25 km from its starting point.
Frequently Asked Questions (FAQ)
Q: Is the Pythagorean theorem only applicable to right-angled triangles?
A: No, the Pythagorean theorem is only directly applicable to right-angled triangles. For other types of triangles, different trigonometric laws (like the Law of Cosines or the Law of Sines) are used.
Q: Are there any triangles where the Pythagorean theorem doesn't work?
A: The Pythagorean theorem only holds true for right-angled triangles. If you try to apply it to a triangle that doesn't have a 90-degree angle, the equation will not be satisfied.
Q: Are there any real-world applications of the Pythagorean theorem beyond those mentioned?
A: Yes, countless applications exist in fields like astronomy (calculating distances between celestial bodies), electronics (calculating impedance in circuits), and even medicine (measuring distances in medical imaging).
Conclusion: The Enduring Power of a Simple Equation
The equation 3² + 4² = 25, while seemingly simple, unveils a profound mathematical relationship underpinning geometry and countless real-world applications. The Pythagorean theorem, embodied by this equation, serves as a cornerstone of mathematical understanding, demonstrating the power and elegance of mathematical principles in explaining and solving problems across diverse disciplines. From construction to computer graphics, navigation to physics, the enduring influence of this fundamental theorem continues to shape our understanding of the world around us. Its exploration extends far beyond simple calculations, offering a gateway to deeper mathematical concepts and showcasing the interconnectedness of various mathematical fields. The journey from a simple equation to a deeper understanding of the Pythagorean theorem highlights the beauty and practicality of mathematical exploration.
Latest Posts
Latest Posts
-
To The 2 3 Power
Sep 11, 2025
-
Calculate Interquartile Range In Excel
Sep 11, 2025
-
Is 2 5 Greater Than 1 3
Sep 11, 2025
-
Gcf Of 20 And 40
Sep 11, 2025
-
Lcm Of 9 And 3
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 3 Square + 4 Square . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.