X Cubed Times X Cubed
saludintensiva
Sep 11, 2025 · 4 min read
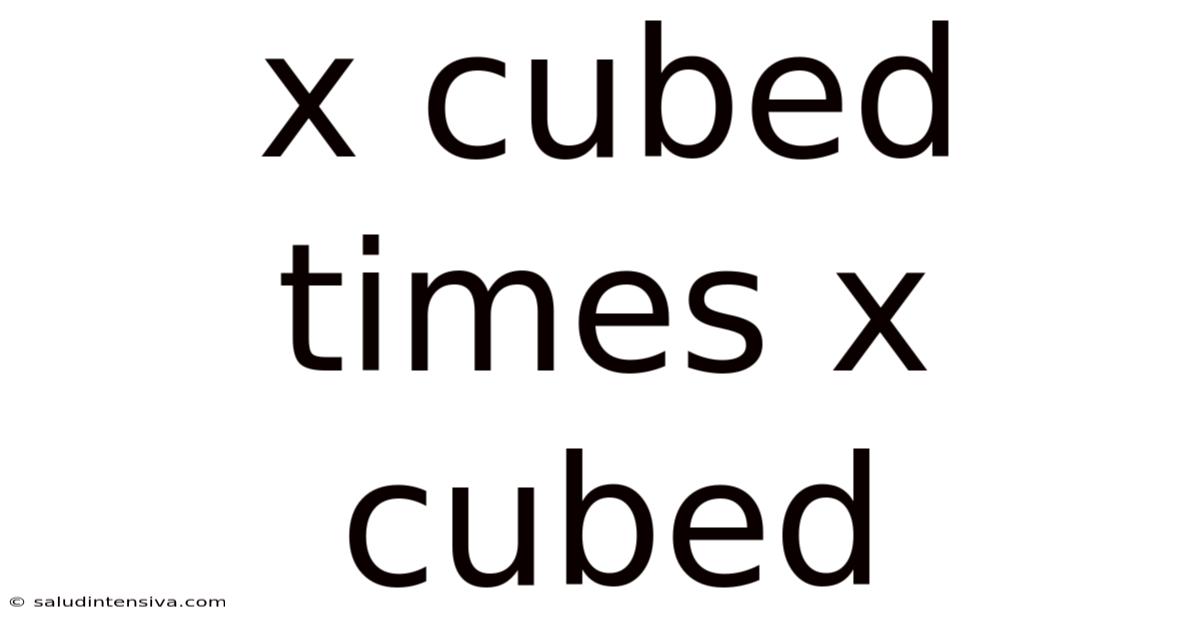
Table of Contents
Understanding x Cubed Times x Cubed: A Deep Dive into Exponential Algebra
This article explores the seemingly simple mathematical expression "x cubed times x cubed," delving deep into its meaning, implications, and applications. We will unravel the underlying principles of exponents and demonstrate how to solve this problem, along with variations and related concepts. This guide is designed for learners of all levels, from those just beginning their algebraic journey to those seeking a more comprehensive understanding of exponential operations. Understanding this fundamental concept is crucial for mastering higher-level mathematics, including calculus and beyond.
Understanding Exponents
Before tackling "x cubed times x cubed," let's solidify our understanding of exponents. An exponent (or power) indicates how many times a base number is multiplied by itself. For example:
- x² (x squared) means x * x
- x³ (x cubed) means x * x * x
- x⁴ (x to the power of four) means x * x * x * x
The small number above and to the right of the base (x) is the exponent. The base number (x) can be any number, variable, or even an expression.
Solving x Cubed Times x Cubed
Now, let's tackle the main problem: x³ * x³. Remembering that x³ means x * x * x, we can rewrite the expression as:
(x * x * x) * (x * x * x)
This is simply a matter of multiplying the x's together. Counting them, we see there are six x's in total. Therefore:
x³ * x³ = x⁶
This demonstrates a fundamental rule of exponents: When multiplying terms with the same base, you add their exponents. In our case, 3 + 3 = 6. This rule can be generalized as: xᵃ * xᵇ = x⁽ᵃ⁺ᵇ⁾
Expanding the Concept: Different Bases and More Complex Expressions
While x³ * x³ is a straightforward example, let's explore more complex scenarios to build a more robust understanding.
Different Bases:
The rule of adding exponents only applies when the bases are identical. If we had, for example, x³ * y³, we cannot simply add the exponents. The expression remains as x³ * y³. There is no further simplification unless we know specific numerical values for x and y.
More Complex Exponents:
The same rule applies with larger exponents. For instance:
-
x⁵ * x⁷ = x¹² (5 + 7 = 12)
-
x¹⁰ * x⁻⁵ = x⁵ (10 + (-5) = 5) This example introduces negative exponents, which represent reciprocals. x⁻ⁿ = 1/xⁿ
-
(x²)³ = x⁶. This illustrates another crucial rule: When raising a power to a power, multiply the exponents. In this case, 2 * 3 = 6. This can be generalized as: (xᵃ)ᵇ = x⁽ᵃ*ᵇ⁾
Expressions with Coefficients:
Let's consider expressions with coefficients (numbers multiplying the variable):
-
2x³ * 3x³ = 6x⁶. Here, we multiply the coefficients (2 * 3 = 6) and add the exponents of the variables (3 + 3 = 6).
-
5x² * 4x⁴ = 20x⁶
The general rule here is to multiply the coefficients and then apply the exponent addition rule for like bases.
Applications in Various Fields
Understanding the principles of exponents, especially this specific case of x³ * x³, has far-reaching applications across numerous fields:
-
Physics: Calculating volumes, areas, and energy levels often involves exponential functions. Understanding how to manipulate expressions like x³ * x³ is crucial for solving complex physics problems, such as those related to gravitational forces or electromagnetic fields.
-
Engineering: Many engineering disciplines rely heavily on mathematical modeling, where exponential functions are essential for representing growth, decay, or other dynamic processes. Calculating stresses, strains, and fluid flow frequently requires manipulating exponential equations.
-
Computer Science: In computer science, the growth rates of algorithms are frequently expressed using exponential notation (e.g., O(n³)). Understanding how to work with exponents is fundamental for analyzing algorithm efficiency.
-
Finance: Compound interest calculations involve exponential functions. Understanding the behavior of exponents helps in forecasting financial growth and understanding the impact of investments over time.
-
Chemistry: Calculating the concentration of reactants and products in chemical reactions often involves exponential equations.
Frequently Asked Questions (FAQ)
Q: What if the exponents are fractions?
A: The rules still apply. For example, x^(1/2) * x^(1/2) = x¹ = x. Remember, x^(1/2) is the square root of x.
Q: What if one term is negative?
A: The rules still hold, but pay attention to the signs. For example: -x³ * x³ = -x⁶. The negative sign remains.
Q: Can I use this concept with variables other than 'x'?
A: Absolutely! The principles are the same regardless of the variable used. a³ * a³ = a⁶, y³ * y³ = y⁶, and so on.
Q: What if I have more than two terms being multiplied?
A: Extend the same principle. For instance: x³ * x³ * x² = x⁸ (3 + 3 + 2 = 8)
Conclusion
Understanding "x cubed times x cubed" goes beyond simply obtaining the answer x⁶. It lays the groundwork for a deeper understanding of exponential algebra, a fundamental concept with far-reaching applications across multiple disciplines. Mastering the rules of exponents, including adding exponents when multiplying like bases and multiplying exponents when raising a power to a power, equips you with a powerful tool for tackling more complex mathematical problems and building a solid foundation in advanced mathematical concepts. The seemingly simple act of multiplying x³ by x³ opens doors to a vast and fascinating world of mathematical possibilities. By consistently practicing and applying these concepts, you’ll not only solve problems efficiently but also develop a deeper intuitive grasp of algebraic relationships.
Latest Posts
Latest Posts
-
Gcf Of 48 And 60
Sep 11, 2025
-
13 Percent In Decimal Form
Sep 11, 2025
-
9 7 9 As A Decimal
Sep 11, 2025
-
7 3 As A Decimal
Sep 11, 2025
-
9 12 Is What Percent
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about X Cubed Times X Cubed . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.