Gcf Of 12 And 54
saludintensiva
Sep 11, 2025 · 6 min read
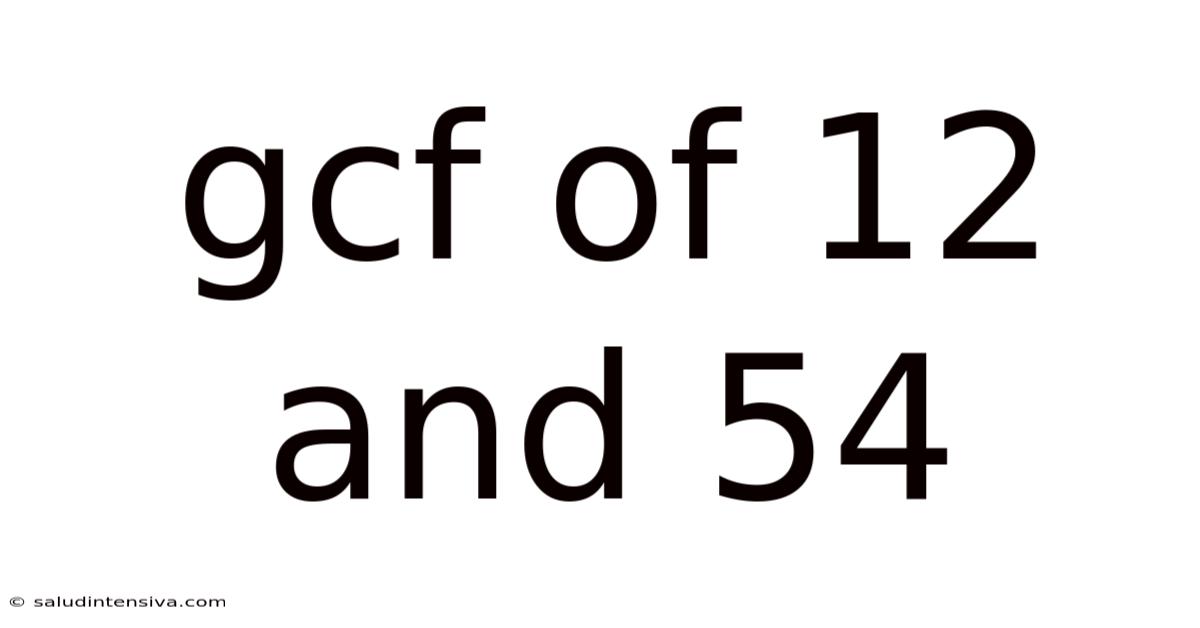
Table of Contents
Unveiling the Greatest Common Factor (GCF) of 12 and 54: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers might seem like a simple arithmetic task. However, understanding the underlying concepts and various methods for calculating the GCF provides a strong foundation for more advanced mathematical concepts. This article will delve deep into finding the GCF of 12 and 54, exploring multiple approaches, explaining the theoretical basis, and answering frequently asked questions. By the end, you'll not only know the GCF of 12 and 54 but also possess a robust understanding of this fundamental mathematical operation.
Understanding the Greatest Common Factor (GCF)
Before we dive into calculating the GCF of 12 and 54, let's clarify what it means. The greatest common factor of two or more integers is the largest positive integer that divides each of the integers without leaving a remainder. In simpler terms, it's the biggest number that perfectly divides both numbers. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12, while the factors of 54 are 1, 2, 3, 6, 9, 18, 27, and 54. The GCF is the largest number present in both lists.
Method 1: Listing Factors
The most straightforward method, especially for smaller numbers like 12 and 54, is to list all the factors of each number and identify the largest common factor.
Factors of 12: 1, 2, 3, 4, 6, 12 Factors of 54: 1, 2, 3, 6, 9, 18, 27, 54
Comparing the two lists, we see that the common factors are 1, 2, 3, and 6. The greatest among these is 6. Therefore, the GCF of 12 and 54 is 6.
Method 2: Prime Factorization
Prime factorization is a more powerful method that works efficiently for larger numbers. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
Prime factorization of 12: 2 x 2 x 3 = 2² x 3 Prime factorization of 54: 2 x 3 x 3 x 3 = 2 x 3³
To find the GCF using prime factorization, identify the common prime factors and their lowest powers. Both 12 and 54 share a 2 and a 3. The lowest power of 2 is 2¹ (or simply 2), and the lowest power of 3 is 3¹. Therefore, the GCF is 2 x 3 = 6.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF, especially for larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers become equal, and that number is the GCF.
Let's apply the Euclidean algorithm to 12 and 54:
- 54 ÷ 12 = 4 with a remainder of 6. We replace 54 with the remainder 6.
- Now we have 12 and 6. 12 ÷ 6 = 2 with a remainder of 0. Since the remainder is 0, the GCF is the last non-zero remainder, which is 6.
Method 4: Using a Ladder Diagram (for visual learners)
The ladder diagram provides a visual representation of the Euclidean algorithm, making it easier to follow, especially for those who benefit from visual aids.
54 | 12
----
48 |
---
6 | 12
---
0
We start by dividing the larger number (54) by the smaller number (12). The remainder (6) becomes the new divisor, and the previous divisor (12) becomes the new dividend. We continue this process until we get a remainder of 0. The last non-zero remainder (6) is the GCF.
The Mathematical Basis: Divisibility Rules and Prime Numbers
Understanding the GCF relies heavily on concepts like divisibility rules and prime numbers. Divisibility rules help us quickly determine if a number is divisible by another without performing the actual division. For example, a number is divisible by 2 if it's an even number, divisible by 3 if the sum of its digits is divisible by 3, and so on. Prime numbers, as previously mentioned, are only divisible by 1 and themselves. The prime factorization method leverages the fundamental theorem of arithmetic, which states that every integer greater than 1 can be uniquely represented as a product of prime numbers.
Applications of GCF in Real Life
While finding the GCF of 12 and 54 might seem abstract, the concept has many practical applications:
- Simplifying Fractions: The GCF is crucial for simplifying fractions to their lowest terms. For example, the fraction 54/12 can be simplified to 9/2 by dividing both the numerator and the denominator by their GCF (6).
- Measurement and Division: When dealing with measurements, finding the GCF can help determine the largest possible equal units for dividing things. For example, if you have 12 meters of red ribbon and 54 meters of blue ribbon, and you want to cut them into equal pieces of the maximum length, the GCF (6) will tell you that you can cut each ribbon into 6-meter lengths.
- Problem Solving: Many word problems in math, particularly those involving ratios, proportions, and distribution, rely on understanding and calculating the GCF.
Frequently Asked Questions (FAQ)
Q1: What if the GCF of two numbers is 1?
A1: If the GCF of two numbers is 1, they are called relatively prime or coprime. This means they share no common factors other than 1.
Q2: Can the GCF of two numbers be larger than either of the numbers?
A2: No, the GCF can never be larger than the smaller of the two numbers.
Q3: Is there a way to find the GCF of more than two numbers?
A3: Yes, you can extend the methods described above to find the GCF of more than two numbers. For prime factorization, you'd find the common prime factors and their lowest powers among all the numbers. For the Euclidean algorithm, you'd repeatedly find the GCF of pairs of numbers until you arrive at the GCF of all the numbers.
Q4: Are there any limitations to the Euclidean algorithm?
A4: The Euclidean algorithm is very efficient, but its computational complexity increases as the numbers get extremely large. For extremely large numbers, more advanced algorithms might be necessary.
Q5: How does the GCF relate to the Least Common Multiple (LCM)?
A5: The GCF and LCM are closely related. For any two positive integers a and b, the product of their GCF and LCM is equal to the product of the two numbers themselves. This relationship is expressed as: GCF(a, b) * LCM(a, b) = a * b. This relationship is useful for finding the LCM of two numbers if you already know their GCF.
Conclusion
Finding the greatest common factor (GCF) of 12 and 54, as we've demonstrated, is a straightforward yet fundamental mathematical operation with far-reaching applications. Whether you use the method of listing factors, prime factorization, the Euclidean algorithm, or the visual ladder diagram, understanding the underlying principles ensures a strong grasp of this crucial concept. The GCF is not merely an isolated arithmetic skill; it forms the bedrock for more complex mathematical problems and real-world applications in various fields. This comprehensive guide not only answers the question of finding the GCF of 12 and 54 but also equips you with the knowledge and tools to tackle similar problems confidently and proficiently. Remember to choose the method that best suits your understanding and the size of the numbers involved.
Latest Posts
Latest Posts
-
Cube Root Of 1 2
Sep 11, 2025
-
6 30 As A Percentage
Sep 11, 2025
-
6 Out Of 10 Percentage
Sep 11, 2025
-
Gcf Of 30 And 40
Sep 11, 2025
-
Is 7 8 Bigger Than 3 4
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Gcf Of 12 And 54 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.