Cube Root Of 1 2
saludintensiva
Sep 11, 2025 · 6 min read
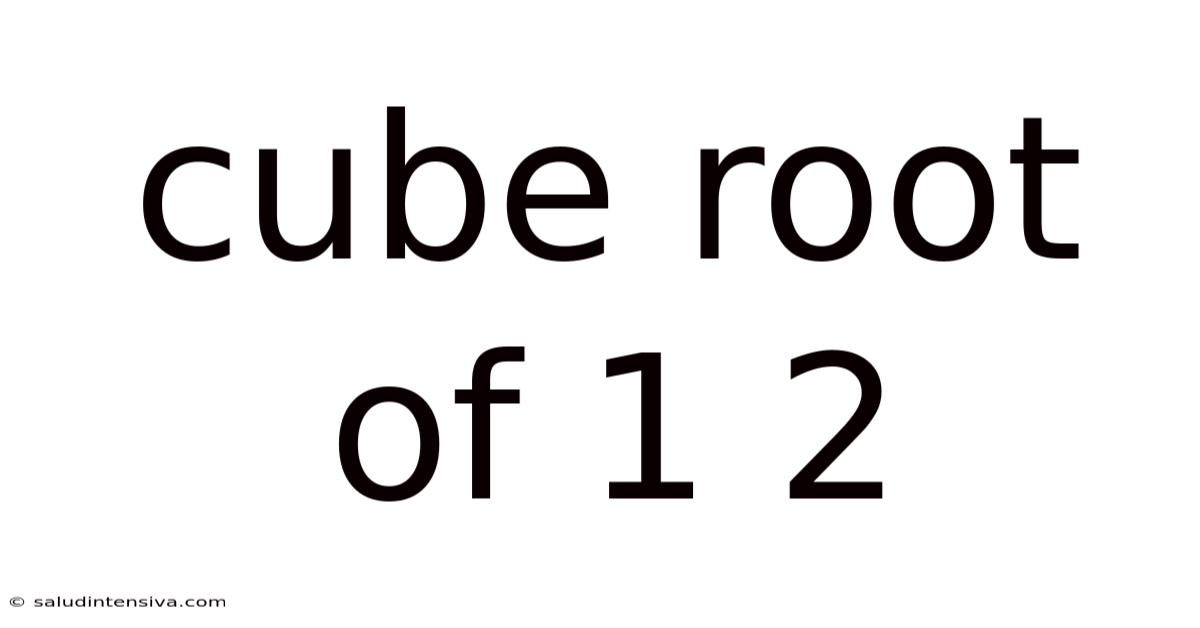
Table of Contents
Unraveling the Cube Root of 12: A Deep Dive into Mathematics
Finding the cube root of 12 might seem like a simple mathematical task, but it offers a fascinating gateway into deeper concepts within algebra and numerical analysis. This article explores various methods for calculating the cube root of 12, ranging from simple estimation techniques to more sophisticated algorithms, providing a comprehensive understanding suitable for students and enthusiasts alike. We'll also delve into the theoretical underpinnings and practical applications of cube roots, ensuring a rich and informative learning experience.
Understanding Cube Roots: The Basics
Before tackling the cube root of 12 specifically, let's solidify our understanding of cube roots in general. The cube root of a number, denoted as ³√x, is a value that, when multiplied by itself three times (cubed), equals x. In other words, if y = ³√x, then y³ = x. For instance, the cube root of 8 is 2 because 2 x 2 x 2 = 8. Unlike square roots, which can have both positive and negative solutions (except for zero), cube roots of positive numbers always yield a single, positive real number. Cube roots of negative numbers result in a single, negative real number.
The cube root of 12, denoted as ³√12, is a real number that, when cubed, equals 12. Because 12 is not a perfect cube (meaning it's not the result of cubing an integer), the cube root of 12 is an irrational number; its decimal representation goes on forever without repeating. This means we can only approximate its value.
Method 1: Estimation and Trial and Error
A straightforward approach to finding an approximate value for ³√12 involves educated guessing and refining our estimate. We know that 2³ = 8 and 3³ = 27. Since 12 lies between 8 and 27, the cube root of 12 must be between 2 and 3. Let's start with a guess of 2.2.
- 2.2³ = 10.648 (too low)
- Let's try 2.3: 2.3³ = 12.167 (close!)
- 2.25³ = 11.39 (closer)
- 2.28³ = 11.85 (getting closer)
- 2.29³ = 12.06 (very close!)
This method demonstrates that ³√12 is approximately 2.289. The accuracy depends on the patience and precision of our guesses. While effective for rough estimations, this method is inefficient for high-precision calculations.
Method 2: Using a Calculator
The simplest and most accurate method for finding the cube root of 12 is to use a scientific calculator or computer software. Most calculators have a dedicated cube root function (often denoted as ³√ or x^(1/3)). Simply input 12 and apply the cube root function. The calculator will provide a precise approximation, typically up to several decimal places. This yields a value of approximately 2.289428485.
Method 3: The Babylonian Method (Newton-Raphson Method)
The Babylonian method, also known as the Newton-Raphson method, is an iterative algorithm that provides increasingly accurate approximations of cube roots. It's based on the principle of successively refining an initial guess using a specific formula.
Steps:
- Initial Guess: Start with an initial guess, x₀, for the cube root of 12. Let's use 2.
- Iteration Formula: Apply the iterative formula: xₙ₊₁ = (1/3) * [2xₙ + (12/xₙ²)] This formula refines the guess in each iteration.
- Iteration: Repeat step 2, substituting the previous approximation (xₙ) into the formula to obtain the next approximation (xₙ₊₁). Continue this process until the desired level of accuracy is reached. The difference between successive approximations will become smaller with each iteration.
Let's perform a few iterations:
- Iteration 1: x₁ = (1/3) * [2(2) + (12/2²)] = 2.3333
- Iteration 2: x₂ = (1/3) * [2(2.3333) + (12/2.3333²)] ≈ 2.29
- Iteration 3: x₃ = (1/3) * [2(2.29) + (12/2.29²)] ≈ 2.2894
As you can see, the approximations converge rapidly towards the actual value of ³√12. The more iterations performed, the more accurate the result will be. This method is computationally efficient and readily adaptable to computer programming for highly precise calculations.
Method 4: Binomial Theorem Approximation
For a more theoretical approach, the binomial theorem can be employed to approximate the cube root of 12. This method involves expressing 12 as a sum or difference of a perfect cube and a smaller number and then using the binomial expansion to approximate the cube root. While more complex than the previous methods, it provides valuable insight into the mathematical properties of cube roots. This approach often requires advanced mathematical knowledge and is beyond the scope of a basic explanation in this article.
Method 5: Logarithms and Exponentials
Another sophisticated approach involves using logarithms and exponentials. The cube root of 12 can be expressed as 12^(1/3). Using logarithmic properties, we can write:
log(³√12) = (1/3)log(12)
By calculating the logarithm of 12 (using a calculator or logarithm tables), multiplying by 1/3, and then finding the antilogarithm (exponential), we can obtain an approximation of ³√12. This method relies on the properties of logarithms and exponential functions and is suitable for those with a strong mathematical background.
The Significance of Cube Roots in Various Fields
The calculation of cube roots is not merely an academic exercise. It holds significant practical implications across diverse fields:
- Engineering: Cube roots are frequently used in engineering calculations, particularly those involving volume, flow rates, and stress analysis. For example, determining the side length of a cube given its volume requires calculating a cube root.
- Physics: In physics, cube roots appear in various formulas related to mechanics, thermodynamics, and fluid dynamics. They are involved in calculations related to gravitational forces, energy, and fluid flow.
- Chemistry: In chemistry, cube roots can be found in formulas related to molarity, density, and reaction rates.
- Finance: While less frequent than square roots, cube roots can find application in certain financial models related to compound interest or investment growth.
- Computer Graphics: Cube roots play a role in 3D graphics and modeling, particularly in transformations and calculations involving vectors and matrices.
Frequently Asked Questions (FAQ)
Q: Is the cube root of 12 a rational or irrational number?
A: The cube root of 12 is an irrational number. Irrational numbers cannot be expressed as a simple fraction of two integers and have non-repeating, non-terminating decimal expansions.
Q: Can I use a simple calculator to find the cube root of 12?
A: Most scientific calculators have a cube root function (often represented as ³√ or x^(1/3)). Simply enter 12 and use the appropriate function.
Q: What is the difference between the cube root and the square root?
A: The square root of a number x (√x) is a value that, when multiplied by itself, equals x. The cube root of a number x (³√x) is a value that, when multiplied by itself three times, equals x.
Q: Are there any negative cube roots?
A: The cube root of a positive number is always a positive real number. The cube root of a negative number is always a negative real number.
Q: Why is the Babylonian method effective for finding cube roots?
A: The Babylonian method is an iterative process that refines an initial guess using a formula derived from calculus. Each iteration brings the approximation closer to the true value, leading to rapid convergence.
Conclusion
Finding the cube root of 12, while appearing simple at first glance, opens doors to a fascinating world of mathematical concepts and techniques. From simple estimation to sophisticated algorithms like the Babylonian method, various approaches can be used to approximate its value. The practical applications of cube roots extend across numerous fields, highlighting their importance beyond purely mathematical contexts. Understanding cube roots is not merely about memorizing formulas; it's about grasping fundamental mathematical principles and their real-world relevance. This article has aimed to provide a comprehensive and accessible explanation, empowering readers with a deeper understanding of this essential mathematical concept.
Latest Posts
Latest Posts
-
Convert 81 F To Celsius
Sep 11, 2025
-
3 Square 4 Square
Sep 11, 2025
-
Half Of 5 1 4
Sep 11, 2025
-
Lcm Of 11 And 2
Sep 11, 2025
-
Gcf Of 60 And 72
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Cube Root Of 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.