1 1/50 As A Decimal
saludintensiva
Sep 19, 2025 · 5 min read
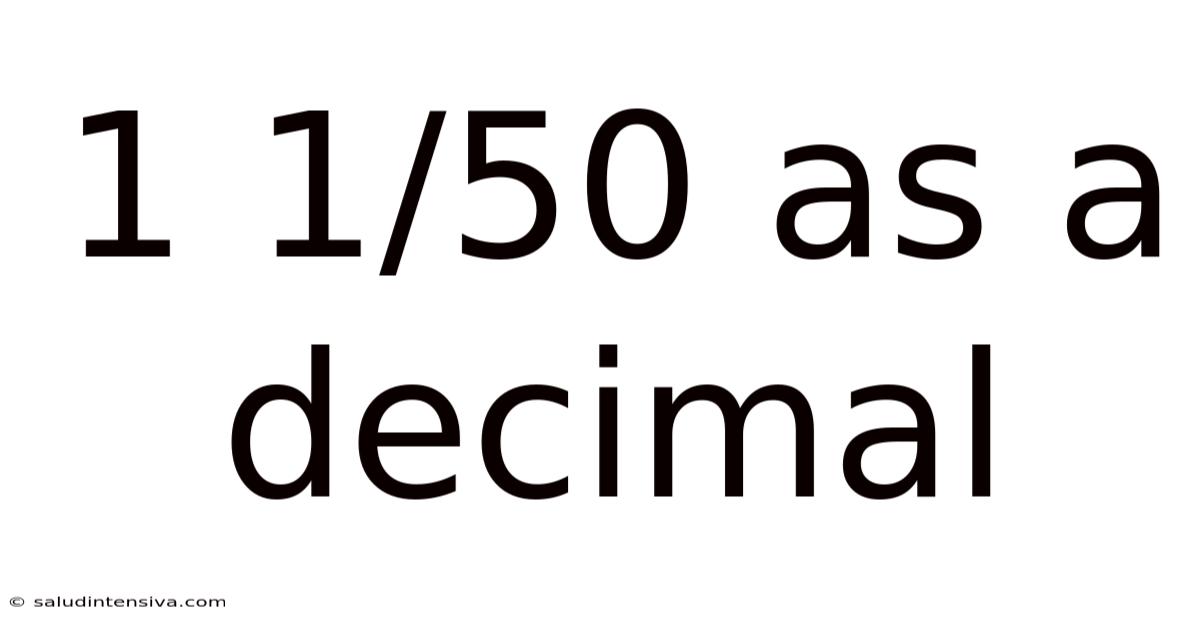
Table of Contents
1 1/50 as a Decimal: A Comprehensive Guide
Converting fractions to decimals is a fundamental skill in mathematics, crucial for various applications from everyday calculations to advanced scientific computations. This article delves into the process of converting the mixed number 1 1/50 into its decimal equivalent, exploring the underlying principles and providing a thorough understanding of the method. We will also touch upon related concepts and address frequently asked questions to solidify your grasp of this important mathematical concept.
Understanding Mixed Numbers and Decimal Representation
Before we dive into the conversion, let's review the basics. A mixed number, like 1 1/50, combines a whole number (1 in this case) and a fraction (1/50). A decimal, on the other hand, represents a number using base-10, with a decimal point separating the whole number part from the fractional part. The conversion process involves transforming the fractional part of the mixed number into its decimal equivalent and then adding it to the whole number.
Method 1: Converting the Fraction to a Decimal
The most straightforward method involves converting the fraction 1/50 to a decimal first. This can be achieved through division:
-
Divide the numerator by the denominator: Divide 1 by 50. This calculation yields 0.02.
-
Add the whole number: Add the whole number part of the mixed number (1) to the decimal equivalent of the fraction (0.02). This gives us the final answer: 1.02.
Therefore, 1 1/50 as a decimal is 1.02.
Method 2: Converting the Mixed Number Directly
We can also directly convert the entire mixed number into an improper fraction and then convert the improper fraction to a decimal. Let's explore this method:
-
Convert to an improper fraction: To convert a mixed number to an improper fraction, multiply the whole number by the denominator of the fraction and add the numerator. Keep the same denominator. In our case:
(1 * 50) + 1 = 51
So, 1 1/50 becomes 51/50.
-
Divide the numerator by the denominator: Now, divide 51 by 50. This gives us 1.02.
Again, we arrive at the same answer: 1.02. This method demonstrates the equivalence between mixed numbers and improper fractions in decimal conversion.
Understanding the Decimal Place Value
It's crucial to understand the place value system in decimals. In the number 1.02:
- 1 represents the ones place (whole number).
- 0 represents the tenths place (one-tenth).
- 2 represents the hundredths place (two-hundredths).
This means that 1.02 is equal to 1 + 0/10 + 2/100. Understanding place value is essential for accurately interpreting and using decimal numbers.
Expanding on Decimal Conversions: More Complex Examples
While 1 1/50 is a relatively simple conversion, let's consider more complex examples to solidify your understanding:
Example 1: Converting 2 3/4 to a decimal
-
Convert to an improper fraction: (2 * 4) + 3 = 11. So, 2 3/4 becomes 11/4.
-
Divide the numerator by the denominator: 11 ÷ 4 = 2.75
Therefore, 2 3/4 as a decimal is 2.75.
Example 2: Converting 5 17/25 to a decimal
-
Convert to an improper fraction: (5 * 25) + 17 = 142. So, 5 17/25 becomes 142/25.
-
Divide the numerator by the denominator: 142 ÷ 25 = 5.68
Therefore, 5 17/25 as a decimal is 5.68.
These examples highlight the consistent application of the method regardless of the complexity of the fraction involved.
The Significance of Decimal Representation
The conversion of fractions to decimals is not merely an academic exercise; it holds significant practical value across numerous fields:
-
Finance: Calculating interest rates, discounts, and profit margins often involves working with decimals.
-
Science: Measurements in scientific experiments are frequently represented as decimals for greater precision.
-
Engineering: Engineering designs and calculations often rely on decimal representation for accurate dimensions and specifications.
-
Everyday life: Calculating percentages, comparing prices, and measuring quantities often require converting fractions to decimals.
Frequently Asked Questions (FAQ)
Q1: What if the fraction doesn't divide evenly?
A1: If the fraction doesn't divide evenly, the resulting decimal will be a repeating decimal (e.g., 1/3 = 0.333...). You might need to round the decimal to a specific number of decimal places based on the context of the problem.
Q2: Can I use a calculator for this conversion?
A2: Yes, using a calculator is a convenient and efficient way to convert fractions to decimals. Most calculators have a division function that directly performs this conversion.
Q3: Why is understanding decimal place value important?
A3: Understanding decimal place value is crucial for accurate calculations and interpretation of results. It ensures you correctly identify the magnitude of each digit in the decimal number and perform calculations accurately.
Q4: What are some real-world applications of converting fractions to decimals?
A4: Real-world applications abound, including calculating percentages (e.g., calculating sales tax or discounts), measuring quantities (e.g., length, weight, volume), and comparing prices. It is also fundamental in various professional fields like finance, engineering, and science.
Q5: Are there any alternative methods for converting fractions to decimals?
A5: While division is the most common and reliable method, you can also use equivalent fractions to simplify the conversion process in some cases. For example, you can convert 1/50 to 2/100 and then easily recognize it as 0.02.
Conclusion
Converting fractions, including mixed numbers, to decimals is a core mathematical skill with broad applications. This article has comprehensively explored the process of converting 1 1/50 to its decimal equivalent (1.02) through two distinct methods, emphasizing the underlying principles and the significance of decimal place value. By mastering this skill, you'll enhance your ability to solve various mathematical problems and navigate a wide range of real-world situations involving numerical calculations. The examples and FAQs provided aim to solidify your understanding and equip you with the confidence to tackle similar conversions independently. Remember, consistent practice is key to mastering any mathematical concept.
Latest Posts
Latest Posts
-
Gcf Of 28 And 14
Sep 19, 2025
-
4 9 As A Percentage
Sep 19, 2025
-
Deg R To Deg C
Sep 19, 2025
-
15 Percent Into A Fraction
Sep 19, 2025
-
Size Of Acre In Yards
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 1 1/50 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.