1 1/8 As A Percent
saludintensiva
Sep 22, 2025 · 6 min read
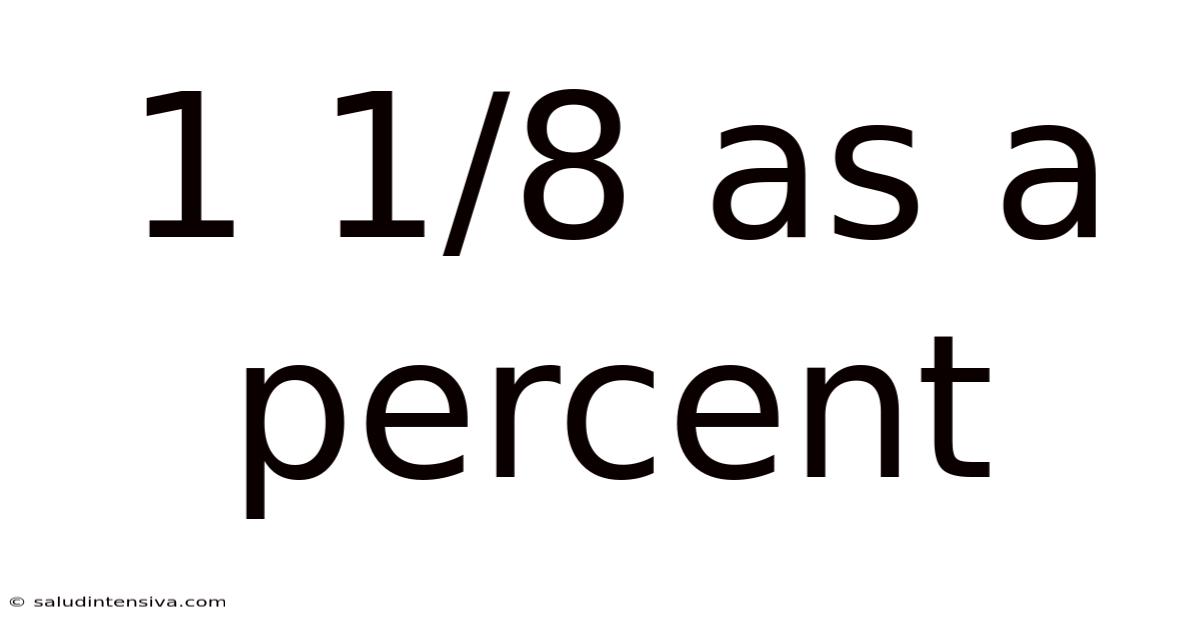
Table of Contents
Decoding 1 1/8 as a Percentage: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics, crucial for various applications in daily life, from calculating discounts and tips to comprehending financial reports and statistical data. This article delves deep into converting the mixed fraction 1 1/8 into a percentage, providing a thorough explanation suitable for all levels of understanding. We’ll not only show you how to do it, but also why the methods work, equipping you with a solid grasp of the underlying principles. This comprehensive guide will explore the different approaches, address common misconceptions, and answer frequently asked questions related to this specific conversion and broader percentage calculations.
Understanding Fractions and Percentages
Before diving into the conversion of 1 1/8, let's refresh our understanding of fractions and percentages.
A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). For example, in the fraction 1/8, 1 is the numerator and 8 is the denominator, indicating one out of eight equal parts.
A percentage is a fraction where the denominator is always 100. It represents a portion of a whole expressed as a number out of 100. The symbol "%" is used to denote percentage. For example, 25% means 25 out of 100, which is equivalent to the fraction 25/100, or simplified, 1/4.
Converting 1 1/8 to an Improper Fraction
The mixed fraction 1 1/8 combines a whole number (1) and a proper fraction (1/8). To convert it into a percentage, it's easier to first convert it into an improper fraction. This means expressing the entire quantity as a single fraction where the numerator is greater than or equal to the denominator.
To do this, we multiply the whole number by the denominator and add the numerator:
(1 x 8) + 1 = 9
The new numerator is 9, and the denominator remains 8. Therefore, 1 1/8 is equivalent to the improper fraction 9/8.
Converting the Improper Fraction to a Decimal
The next step involves converting the improper fraction 9/8 into a decimal. This is done by dividing the numerator (9) by the denominator (8):
9 ÷ 8 = 1.125
This decimal, 1.125, represents the same quantity as 1 1/8.
Converting the Decimal to a Percentage
Finally, to express 1.125 as a percentage, we multiply the decimal by 100:
1.125 x 100 = 112.5
Therefore, 1 1/8 is equal to 112.5%. This indicates that 1 1/8 represents 112.5 parts out of 100.
Alternative Method: Converting the Fraction Directly to a Percentage
While the previous method is straightforward, we can also convert the mixed fraction directly to a percentage without converting to an improper fraction first. Let's break it down:
- Convert the fractional part to a decimal: 1/8 = 0.125
- Add the whole number: 1 + 0.125 = 1.125
- Multiply by 100 to convert to percentage: 1.125 x 100 = 112.5%
This method achieves the same result, offering a slightly shorter calculation path for those comfortable working with decimals directly.
Understanding the Meaning of 112.5%
It's important to understand the significance of a percentage exceeding 100%. While percentages typically represent a portion of a whole (less than or equal to 100%), a percentage greater than 100% signifies a quantity exceeding the original whole. In this case, 112.5% of a quantity means 1.125 times that quantity. For example, if you have a quantity of 100, then 112.5% of that quantity would be 112.5. This concept is often used in contexts like growth, increase, or comparisons where one value is larger than another.
Real-World Applications
The ability to convert fractions to percentages is valuable in numerous everyday situations. Here are some examples:
- Calculating Percentage Increase/Decrease: If a stock price increases from $8 to $9, the percentage increase is calculated using the concept explained above.
- Understanding Financial Reports: Financial statements often present data as percentages for easier interpretation and comparison.
- Calculating Discounts and Sales Tax: Knowing how to convert fractions and decimals into percentages is essential for determining the final price after discounts or adding sales taxes.
- Interpreting Statistical Data: Statistics frequently use percentages to represent proportions and trends in data sets.
Frequently Asked Questions (FAQ)
Q1: Can I convert any mixed fraction to a percentage using this method?
A1: Yes, absolutely. This method applies to all mixed fractions. Simply follow the steps: convert to an improper fraction, then to a decimal, and finally multiply by 100 to get the percentage.
Q2: What if the fraction has a larger denominator? Does the process change?
A2: No, the process remains the same. While the calculations might become slightly more complex with larger denominators, the underlying principles remain consistent. You'll still convert the mixed fraction to an improper fraction, divide to get the decimal, and then multiply by 100 to express it as a percentage.
Q3: Why is it important to understand the conversion of fractions to percentages?
A3: Understanding this conversion is fundamental for comprehending and applying mathematical concepts in various real-world scenarios, from everyday finance to advanced statistical analysis. It helps in interpreting data, calculating increases or decreases, and making informed decisions.
Q4: Are there any online tools or calculators that can help with this conversion?
A4: While many online tools and calculators can assist with fraction-to-percentage conversions, understanding the underlying methodology is crucial for developing a strong mathematical foundation and for troubleshooting if you encounter unexpected results.
Q5: Can I express 112.5% as a mixed fraction?
A5: Yes, you can reverse the process. 112.5% is equivalent to 1.125. To convert this decimal back to a fraction, write it as 1125/1000. Then, simplify the fraction by dividing both the numerator and denominator by their greatest common divisor, which is 125. This will give you 9/8, which is the same as the original mixed fraction 1 1/8.
Conclusion
Converting 1 1/8 to a percentage involves a straightforward process that reinforces our understanding of fractions, decimals, and percentages. By mastering this conversion, you build a strong foundation in numerical literacy, essential for tackling more complex mathematical challenges and real-world applications. Remember that the key steps involve converting the mixed fraction to an improper fraction, converting the improper fraction to a decimal, and finally multiplying the decimal by 100 to obtain the percentage equivalent. Understanding the meaning of percentages greater than 100% is equally important for interpreting results accurately in various contexts. This comprehensive guide provides a solid understanding of the concept and equips you with the skills to tackle similar conversions with confidence.
Latest Posts
Latest Posts
-
Tens Of Thousands Of Dollars
Sep 22, 2025
-
Convert 95 C To F
Sep 22, 2025
-
Is 3 6 Equal To 1 2
Sep 22, 2025
-
Rate Me 1 Through 10
Sep 22, 2025
-
Business Days In November 2024
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 1 1/8 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.