1 1 8 Simplified Fraction
saludintensiva
Sep 22, 2025 · 5 min read
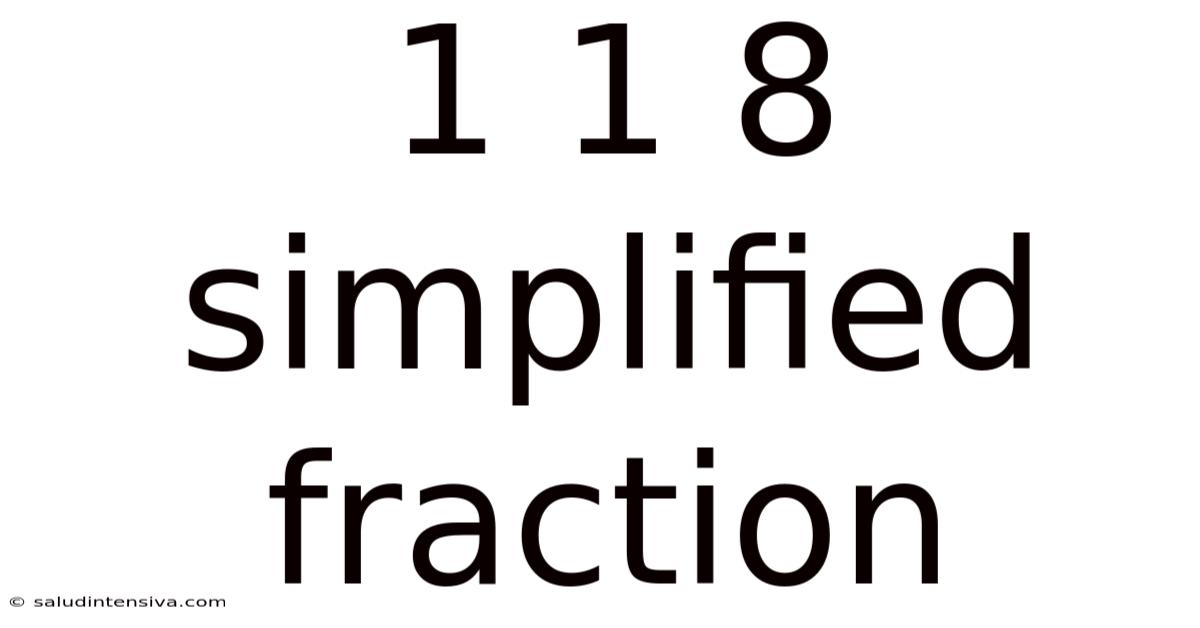
Table of Contents
Unveiling the Simplicity of 11/8: A Comprehensive Guide to Fraction Simplification
Understanding fractions is a cornerstone of mathematics, crucial for everything from baking a cake to calculating complex engineering designs. This article delves into the simplification of the fraction 11/8, explaining the process step-by-step, exploring the underlying mathematical concepts, and answering frequently asked questions. We'll also touch upon the broader context of fraction simplification and its importance in various fields. By the end, you'll not only know how to simplify 11/8 but also possess a strong foundation in fraction manipulation.
What is a Fraction and Why Simplify?
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). For instance, in the fraction 11/8, 11 is the numerator and 8 is the denominator. This means we have 11 parts out of a total of 8 parts. Since we have more parts than the whole allows, this is an improper fraction.
Simplifying a fraction means reducing it to its lowest terms. This doesn't change the value of the fraction; it simply makes it easier to understand and work with. Simplified fractions are more manageable in calculations and provide a clearer representation of the quantity involved. Think of it like reducing a complex recipe to its essential ingredients – the result is the same, but the process is streamlined.
Simplifying 11/8: A Step-by-Step Guide
The fraction 11/8 is an improper fraction, meaning the numerator (11) is larger than the denominator (8). Before simplification, we need to convert it into a mixed number, which combines a whole number and a proper fraction.
1. Conversion to Mixed Number:
To convert 11/8 to a mixed number, we perform a division:
11 ÷ 8 = 1 with a remainder of 3
This means 11/8 is equivalent to 1 and 3/8. The whole number (1) represents the number of times 8 goes into 11 completely, and the remainder (3) becomes the numerator of the new proper fraction, with the denominator remaining the same (8).
2. Simplifying the Proper Fraction (if possible):
Now we examine the proper fraction 3/8. To simplify a fraction, we need to find the greatest common divisor (GCD) of the numerator and the denominator. The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder.
In this case, the GCD of 3 and 8 is 1. Since the GCD is 1, the fraction 3/8 is already in its simplest form. It cannot be further simplified.
3. Final Result:
Therefore, the simplified form of 11/8 is 1 3/8. This mixed number represents one whole and three-eighths of another.
The Importance of Finding the Greatest Common Divisor (GCD)
Finding the GCD is paramount in simplifying fractions. Several methods exist to determine the GCD, including:
-
Listing Factors: List all the factors (numbers that divide evenly) of both the numerator and the denominator. The largest number that appears in both lists is the GCD. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The GCD of 12 and 18 is 6.
-
Prime Factorization: Break down both the numerator and the denominator into their prime factors (numbers divisible only by 1 and themselves). The GCD is the product of the common prime factors raised to the lowest power. For example, the prime factorization of 12 is 2² x 3, and the prime factorization of 18 is 2 x 3². The common prime factors are 2 and 3. The lowest power of 2 is 2¹, and the lowest power of 3 is 3¹. Therefore, the GCD is 2 x 3 = 6.
-
Euclidean Algorithm: This is a more efficient method for larger numbers. It involves repeatedly dividing the larger number by the smaller number and replacing the larger number with the remainder until the remainder is 0. The last non-zero remainder is the GCD.
Beyond 11/8: Practical Applications of Fraction Simplification
The ability to simplify fractions isn't just an academic exercise; it's a vital skill with widespread applications:
-
Cooking and Baking: Recipes often use fractions to indicate ingredient quantities. Simplifying fractions makes it easier to measure and understand the proportions.
-
Construction and Engineering: Precise measurements are crucial in these fields. Simplifying fractions ensures accuracy and simplifies calculations.
-
Finance: Working with percentages and proportions in financial calculations often involves simplifying fractions to understand the relative values.
-
Data Analysis: Simplifying fractions can make interpreting data easier and clearer when dealing with proportions and ratios.
-
Everyday Life: From sharing items equally to understanding discounts, the ability to work with and simplify fractions is a useful life skill.
Frequently Asked Questions (FAQs)
Q: Can I simplify a fraction by dividing the numerator and denominator by any number?
A: No, you must divide both the numerator and the denominator by their greatest common divisor (GCD). Dividing by any other common factor will simplify the fraction, but not to its lowest terms.
Q: What if the GCD is 1?
A: If the GCD of the numerator and denominator is 1, the fraction is already in its simplest form and cannot be simplified further.
Q: Is there a difference between simplifying an improper fraction and a proper fraction?
A: The process is similar, but improper fractions must first be converted to mixed numbers before simplifying the fractional part.
Q: Why is simplifying fractions important?
A: Simplifying fractions makes them easier to understand, compare, and use in calculations. It provides a clearer representation of the quantity and streamlines mathematical processes.
Conclusion
Simplifying fractions is a fundamental skill in mathematics with wide-ranging practical applications. While the process might seem straightforward, understanding the underlying concepts, like the greatest common divisor, is crucial for mastering it. The simplification of 11/8 to 1 3/8 exemplifies the process, demonstrating how converting an improper fraction to a mixed number and finding the GCD leads to a more concise and easily understandable representation of the fraction's value. By grasping these concepts and practicing regularly, you'll gain confidence and proficiency in handling fractions, making them less daunting and more valuable tools in your mathematical arsenal. Remember, practice makes perfect – so keep working with fractions to build a strong foundation for future mathematical endeavors.
Latest Posts
Latest Posts
-
6 5 Percent As A Decimal
Sep 22, 2025
-
1 Kilo To Troy Oz
Sep 22, 2025
-
How Many Months 90 Days
Sep 22, 2025
-
What Is 3 15 Simplified
Sep 22, 2025
-
80 Deg F To C
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 1 1 8 Simplified Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.