1 1 8 X 3
saludintensiva
Sep 12, 2025 · 6 min read
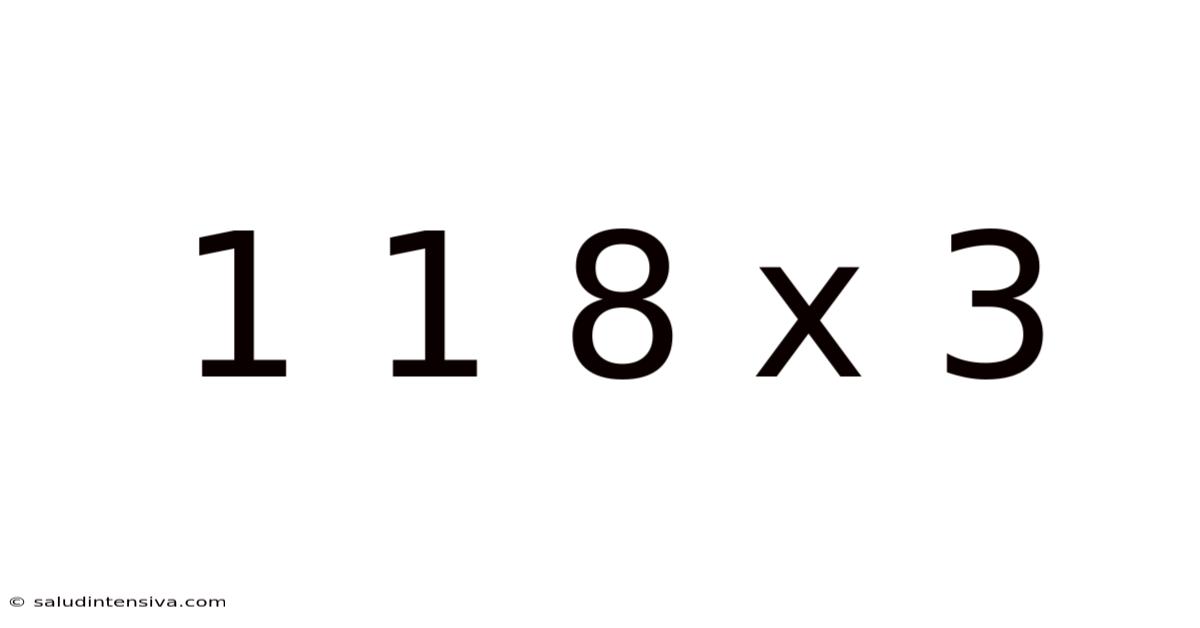
Table of Contents
Decoding 118 x 3: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple multiplication problem, 118 x 3, but expands far beyond a basic calculation. We'll delve into the underlying mathematical principles, explore different methods of solving it, discuss its practical applications, and even touch upon the broader implications of multiplication in various fields. Understanding this seemingly straightforward equation unlocks a deeper appreciation for the fundamental building blocks of mathematics and its pervasive influence on our world.
Introduction: More Than Just Numbers
At first glance, 118 x 3 appears as a straightforward arithmetic problem. However, its simplicity belies a wealth of mathematical concepts and practical applications. This problem offers a perfect entry point to understand multiplication's core principles, various solution methods, and its real-world relevance in diverse fields ranging from everyday budgeting to advanced engineering. By the end of this exploration, you’ll not only know the answer to 118 x 3 but also gain a much deeper understanding of multiplication itself.
Method 1: The Standard Algorithm
The most common approach to solving 118 x 3 is the standard multiplication algorithm taught in elementary schools. This method involves multiplying each digit of 118 by 3 individually and then adding the results, carrying over when necessary.
- Multiply the ones digit: 3 x 8 = 24. Write down '4' and carry-over '2'.
- Multiply the tens digit: 3 x 1 = 3. Add the carry-over '2': 3 + 2 = 5. Write down '5'.
- Multiply the hundreds digit: 3 x 1 = 3. Write down '3'.
- Combine the results: The final answer is 354.
Therefore, 118 x 3 = 354.
Method 2: Distributive Property
The distributive property of multiplication states that a(b + c) = ab + ac. We can apply this to solve 118 x 3 by breaking down 118 into smaller, easier-to-manage numbers.
- Break down 118: We can express 118 as 100 + 10 + 8.
- Apply the distributive property: 3 x (100 + 10 + 8) = (3 x 100) + (3 x 10) + (3 x 8)
- Calculate each part: 300 + 30 + 24 = 354
This method demonstrates the underlying principle of multiplication, showing how it distributes across addition. It's particularly useful for mental calculations and for understanding the logic behind multiplication.
Method 3: Repeated Addition
Multiplication can be fundamentally understood as repeated addition. 118 x 3 simply means adding 118 three times:
118 + 118 + 118 = 354
While this method is straightforward, it becomes less efficient with larger numbers. However, it reinforces the core concept of multiplication as a shortcut for repeated addition.
Method 4: Lattice Multiplication (for Visual Learners)
Lattice multiplication is a visual method that can be helpful for understanding the process and reducing errors, especially with larger numbers. While slightly more complex to set up, it offers a clear way to see the individual multiplication steps.
- Create a lattice: Draw a grid with two rows (for the digits of 118) and one column (for the multiplier 3).
- Multiply and place digits: Multiply each digit of 118 by 3 and place the result diagonally within the corresponding cell. For example, 3 x 8 = 24, so place '2' in the top half and '4' in the bottom half of the cell.
- Add diagonally: Add the numbers along each diagonal, carrying over when necessary.
- Read the result: The final answer will be read from top to bottom along the outer edge of the lattice.
This visual approach can be particularly beneficial for learners who prefer a more graphical representation of the calculation.
The Mathematical Principles Behind 118 x 3
This seemingly simple problem embodies several key mathematical principles:
- Commutative Property: While not directly used in solving 118 x 3, the commutative property of multiplication (a x b = b x a) is a fundamental concept. It demonstrates that the order of the numbers does not affect the product. Thus, 118 x 3 is the same as 3 x 118.
- Associative Property: This property allows for regrouping numbers in multiplication without affecting the result. For instance, if we had a more complex problem involving multiple multiplications, the associative property would be crucial for simplifying the calculation.
- Distributive Property (as discussed above): This property is particularly relevant here, showcasing how multiplication interacts with addition.
- Identity Property: The identity property of multiplication states that any number multiplied by 1 remains unchanged. While not directly present in 118 x 3, it's an important foundational concept in the number system.
Real-World Applications of Multiplication
Multiplication is far from a theoretical exercise; it's a fundamental tool used in countless real-world scenarios:
- Everyday Budgeting: Calculating the total cost of multiple items, determining monthly expenses, or calculating the cost of bulk purchases all rely on multiplication. For example, if you need to buy three items costing $118 each, multiplication helps you quickly determine the total cost.
- Construction and Engineering: Calculating the amount of materials needed for a project, determining the area or volume of structures, and many other engineering calculations rely heavily on multiplication.
- Cooking and Baking: Scaling recipes, calculating ingredient quantities, and adjusting portion sizes all involve multiplication.
- Science and Technology: Numerical modelling, data analysis, and many scientific calculations use multiplication as a cornerstone.
- Finance and Business: Calculating profits, losses, interest, and many other financial computations are based on multiplication.
- Computer Programming: Multiplication is a core arithmetic operation in programming, used extensively in algorithms and calculations.
Extending the Concept: Beyond 118 x 3
While we've focused on 118 x 3, the principles discussed apply to any multiplication problem. Understanding these methods and principles empowers you to solve more complex problems efficiently and accurately. For instance, consider the following extensions:
- Multiplying larger numbers: The same techniques can be applied to multiply larger numbers, requiring only a bit more patience and careful execution.
- Multiplying decimals and fractions: The principles of multiplication extend to decimals and fractions, though the procedures might differ slightly.
- Algebraic multiplication: In algebra, multiplication involves variables and expressions, requiring an understanding of the rules of exponents and the distributive property.
Frequently Asked Questions (FAQ)
Q: What are some common mistakes people make when multiplying?
A: Common mistakes include errors in carrying over digits, misplacing digits in the answer, and not understanding the distributive property. Practice and careful attention to detail are crucial for accuracy.
Q: Are there any shortcuts for multiplying numbers mentally?
A: Yes, there are several mental math techniques. Breaking down numbers using the distributive property, rounding, and using number properties can help simplify mental calculations.
Q: Why is learning multiplication important?
A: Multiplication is a fundamental mathematical skill essential for various academic, professional, and everyday life applications. A strong understanding of multiplication opens doors to more advanced mathematical concepts and real-world problem-solving.
Conclusion: The Power of Multiplication
The seemingly simple equation, 118 x 3, provides a gateway to understanding the profound significance of multiplication. From its foundational principles to its widespread practical applications, multiplication serves as a cornerstone of mathematics and a vital tool for navigating our world. By mastering multiplication techniques and understanding its underlying logic, you equip yourself with a powerful skill that will continue to benefit you throughout your life. The answer to 118 x 3 is 354, but the true value lies in the understanding gained throughout this exploration. So keep practicing, exploring, and discovering the incredible power of multiplication!
Latest Posts
Latest Posts
-
20 3 As A Mixed Number
Sep 12, 2025
-
Is 1 4 Bigger Than 3 16
Sep 12, 2025
-
What Time Is 14 53
Sep 12, 2025
-
76 Graus Fahrenheit Em Celsius
Sep 12, 2025
-
Year Over Year Percentage Calculator
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 1 1 8 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.