1 17/20 As A Percent
saludintensiva
Sep 10, 2025 · 5 min read
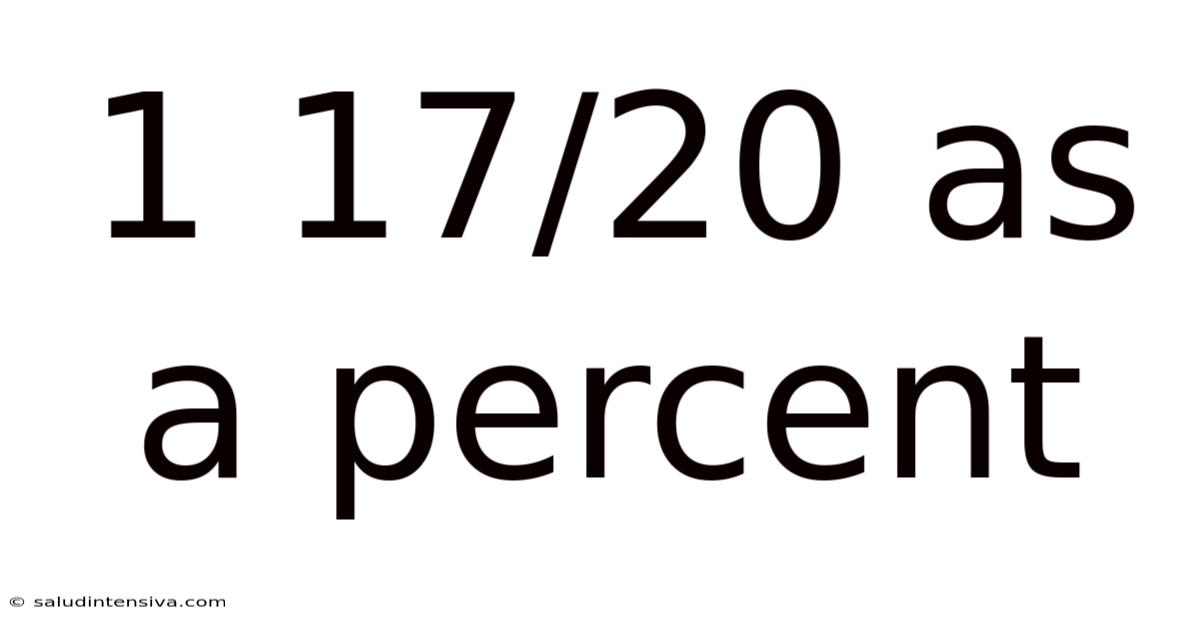
Table of Contents
1 17/20 as a Percent: A Comprehensive Guide to Converting Mixed Numbers to Percentages
Converting fractions and mixed numbers into percentages is a fundamental skill in mathematics, essential for various applications from everyday calculations to advanced statistical analysis. This comprehensive guide will delve into the process of converting the mixed number 1 17/20 into a percentage, explaining the underlying principles and providing multiple approaches to solve this problem. We'll also explore related concepts and answer frequently asked questions to ensure a thorough understanding of this important mathematical concept.
Understanding the Basics: Fractions, Decimals, and Percentages
Before diving into the conversion, let's clarify the relationship between fractions, decimals, and percentages. They are all different ways of representing parts of a whole.
- Fractions: Represent a part of a whole as a ratio of two numbers (numerator/denominator). For example, 1/2 represents one out of two equal parts.
- Decimals: Represent a part of a whole using the base-10 system. For instance, 0.5 is equivalent to 1/2.
- Percentages: Represent a part of a whole as a fraction of 100. The symbol "%" denotes "per hundred". So, 50% means 50 out of 100, which is equivalent to 1/2 or 0.5.
The key to converting between these forms is understanding that they are all interchangeable. We can convert from one form to another using simple arithmetic operations.
Method 1: Converting the Mixed Number to an Improper Fraction
The first step in converting 1 17/20 to a percentage involves transforming the mixed number into an improper fraction. A mixed number combines a whole number and a fraction (e.g., 1 17/20). An improper fraction has a numerator larger than or equal to its denominator (e.g., 37/20).
To convert 1 17/20 to an improper fraction, we follow these steps:
- Multiply the whole number by the denominator: 1 * 20 = 20
- Add the numerator to the result: 20 + 17 = 37
- Keep the same denominator: 20
Therefore, 1 17/20 is equivalent to the improper fraction 37/20.
Method 2: Converting the Improper Fraction to a Decimal
Now that we have the improper fraction 37/20, we can convert it to a decimal by performing the division:
37 ÷ 20 = 1.85
This decimal, 1.85, represents the same quantity as 1 17/20 and 37/20.
Method 3: Converting the Decimal to a Percentage
The final step is to convert the decimal 1.85 to a percentage. To do this, we multiply the decimal by 100:
1.85 * 100 = 185
Therefore, 1 17/20 is equal to 185%.
A Summary of the Conversion Process
To reiterate the steps involved in converting 1 17/20 to a percentage:
- Convert the mixed number to an improper fraction: 1 17/20 = 37/20
- Convert the improper fraction to a decimal: 37/20 = 1.85
- Convert the decimal to a percentage: 1.85 * 100 = 185%
Therefore, the answer is 185%.
Understanding the Result: What does 185% mean?
A percentage greater than 100% indicates that the value represents more than the whole. In this context, 185% means that the quantity represented by 1 17/20 is 185% of a single unit or 1.85 times the size of a single unit. This is often encountered when dealing with growth rates, increases, or quantities exceeding the original baseline. For example, if a company's profit increased by 1 17/20 times its previous profit, we would say that the profit increased by 185%.
Alternative Approach: Direct Conversion from Mixed Number to Percentage
While the stepwise approach detailed above is methodical and helps understand the underlying principles, there's a slightly more concise way to convert directly from a mixed number to a percentage. Let's examine this approach:
- Convert the fractional part to a decimal: 17/20 = 0.85
- Add the whole number: 1 + 0.85 = 1.85
- Multiply by 100 to obtain the percentage: 1.85 * 100 = 185%
This method achieves the same result but streamlines the process by combining steps.
Practical Applications of Percentage Conversions
The ability to convert fractions and mixed numbers into percentages is crucial in many real-world scenarios, including:
- Finance: Calculating interest rates, profit margins, and returns on investment.
- Statistics: Representing data as percentages in charts and graphs.
- Retail: Calculating discounts, sales tax, and markups.
- Science: Expressing experimental results and data analysis.
- Everyday Life: Calculating tips, splitting bills, and understanding proportions.
Frequently Asked Questions (FAQ)
Q1: Can I convert any mixed number to a percentage?
A1: Yes, you can convert any mixed number to a percentage using the methods described above. The process remains the same regardless of the specific values of the whole number and fraction.
Q2: What if the fraction part of the mixed number has a denominator that isn't easily divisible by 10, 100, or 1000?
A2: Even if the denominator is not easily divisible by powers of 10, the process is the same. You will simply get a decimal with more digits after the decimal point. You can round the decimal to the desired number of significant figures after converting to a percentage.
Q3: What if the mixed number is negative?
A3: If the mixed number is negative (e.g., -1 17/20), the resulting percentage will also be negative. Follow the same steps, and the final answer will be -185%.
Q4: Are there any online calculators that can perform this conversion?
A4: Yes, numerous online calculators are available to perform this type of conversion. Simply search for "mixed number to percentage calculator" to find a suitable tool. However, understanding the underlying principles is crucial for problem-solving and critical thinking.
Conclusion
Converting 1 17/20 to a percentage involves a straightforward process that hinges on understanding the relationships between fractions, decimals, and percentages. By transforming the mixed number into an improper fraction, then a decimal, and finally a percentage, we arrive at the answer of 185%. This seemingly simple calculation is a cornerstone of numerous mathematical applications, highlighting the importance of mastering these fundamental conversion techniques. The ability to fluently translate between these different representations of numerical values is essential for success in various academic and professional fields. Remember to practice these steps to build confidence and proficiency in percentage calculations.
Latest Posts
Latest Posts
-
10 6 As A Decimal
Sep 10, 2025
-
31 40 As A Decimal
Sep 10, 2025
-
38 40 As A Percent
Sep 10, 2025
-
Half Of 3 1 2 Inches
Sep 10, 2025
-
1 4 As A Whole Number
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 1 17/20 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.