1 17 As A Percentage
saludintensiva
Sep 17, 2025 · 5 min read
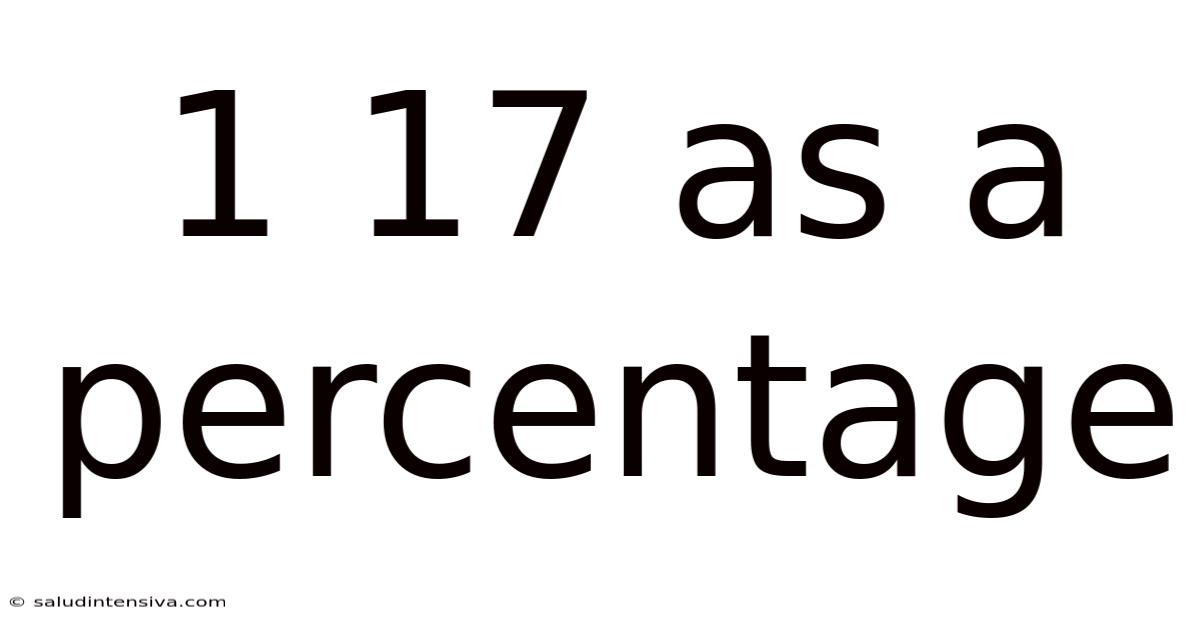
Table of Contents
1/17 as a Percentage: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics with broad applications in everyday life, from calculating discounts and tips to comprehending data in various fields. This comprehensive guide will delve into the process of converting the fraction 1/17 into a percentage, explaining the methodology in detail, exploring related concepts, and addressing frequently asked questions. We'll explore different methods to achieve this conversion, ensuring a thorough understanding for readers of all levels.
Understanding Fractions and Percentages
Before we tackle the specific conversion of 1/17, let's review the basics. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates the number of parts you have, while the denominator indicates the total number of parts the whole is divided into.
A percentage is a fraction expressed as a portion of 100. It signifies a rate, ratio, or proportion per hundred. The symbol "%" is used to denote a percentage. For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or 1/2.
The core relationship between fractions and percentages is that a percentage is simply a fraction with a denominator of 100. Therefore, converting a fraction to a percentage involves finding an equivalent fraction with a denominator of 100, or using a different mathematical approach.
Method 1: Direct Conversion Using Division
The most straightforward method for converting a fraction to a percentage is through division. This method works for any fraction, including 1/17.
-
Divide the numerator by the denominator: Divide 1 by 17. This will give you a decimal value. 1 ÷ 17 ≈ 0.0588235
-
Multiply the decimal by 100: To express the decimal as a percentage, multiply the result by 100. 0.0588235 × 100 ≈ 5.88235%
-
Round to the desired precision: Since percentages are often rounded for practical purposes, you can round the result to a specific number of decimal places. For example, rounding to two decimal places gives us approximately 5.88%.
Therefore, 1/17 is approximately 5.88%. Remember that this is an approximation because the decimal representation of 1/17 is non-terminating (it goes on infinitely).
Method 2: Finding an Equivalent Fraction with a Denominator of 100
While less practical for a fraction like 1/17, this method helps illustrate the fundamental relationship between fractions and percentages. The goal is to find a number that, when multiplied by 17, gives 100 (or a close approximation). Unfortunately, there isn't a whole number that satisfies this condition exactly. However, we can use a calculator to get a close approximation:
-
Determine the multiplier: Divide 100 by the denominator (17): 100 ÷ 17 ≈ 5.882
-
Multiply both the numerator and the denominator by this approximate multiplier:
- Numerator: 1 × 5.882 ≈ 5.882
- Denominator: 17 × 5.882 ≈ 99.994 (very close to 100)
-
Express as a percentage: The resulting fraction is approximately 5.882/100, which is approximately 5.882%. Again, rounding to two decimal places gives us 5.88%.
This method highlights the conceptual link between fractions and percentages but is less efficient for fractions with denominators that don't easily yield multiples of 100.
Understanding the Remainder and Precision
It's crucial to understand that the conversion of 1/17 to a percentage results in a non-terminating decimal. This means the decimal representation goes on infinitely without repeating. The precision of the percentage depends on how many decimal places you round to. Rounding to two decimal places provides a practical approximation for most applications, but for higher precision, you would need to include more decimal places.
Applications of Percentage Conversions
Converting fractions to percentages is incredibly useful in many real-world situations:
- Financial Calculations: Calculating interest rates, discounts, tax rates, and profit margins all involve working with percentages.
- Data Analysis: Percentages are used extensively to represent data proportions in graphs, charts, and reports.
- Probability and Statistics: Probabilities are often expressed as percentages.
- Everyday Life: Understanding percentages helps in making informed decisions related to shopping, budgeting, and other daily activities.
Frequently Asked Questions (FAQ)
Q: Why isn't the percentage for 1/17 a whole number?
A: Because 17 is not a factor of 100. Only fractions whose denominators are factors of 100 (e.g., 1/2, 1/4, 1/5, 1/10, 1/20, 1/25, 1/50, 1/100) will convert to whole number percentages. Fractions with other denominators will result in decimal percentages.
Q: What is the most accurate way to represent 1/17 as a percentage?
A: There is no single "most accurate" way. The accuracy depends on the number of decimal places you use. The more decimal places you use, the more precise the representation, but it also becomes less practical for everyday use. 5.88% is a sufficiently accurate approximation for most purposes.
Q: Can I use a calculator to convert any fraction to a percentage?
A: Yes, a calculator is a very helpful tool for this conversion. Simply divide the numerator by the denominator, and then multiply the result by 100.
Q: Are there any other methods to convert fractions to percentages?
A: While the division method is the most efficient, you can also use proportion techniques or convert the fraction into a decimal and then multiply by 100. The key is to find an equivalent fraction with a denominator of 100, though this is not always practical.
Conclusion
Converting 1/17 to a percentage requires dividing 1 by 17 and multiplying the result by 100. This yields an approximate percentage of 5.88%. Understanding this conversion process is crucial for various applications in mathematics, finance, and daily life. Remember that the result is an approximation due to the non-terminating decimal nature of the fraction. Choosing the appropriate level of precision depends on the context of the problem. By mastering this fundamental concept, you'll be better equipped to handle numerous situations that involve working with fractions and percentages. The methods outlined above provide a comprehensive understanding of this important mathematical skill, enabling you to confidently tackle similar conversions in the future.
Latest Posts
Latest Posts
-
260 Billion In Scientific Notation
Sep 17, 2025
-
Answer To A Multiplication Problem
Sep 17, 2025
-
2 3 Plus 1 6
Sep 17, 2025
-
What Is 200db Depreciation Method
Sep 17, 2025
-
4 To Power Of 8
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 1 17 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.