1 2 1 3 2
saludintensiva
Sep 12, 2025 · 6 min read
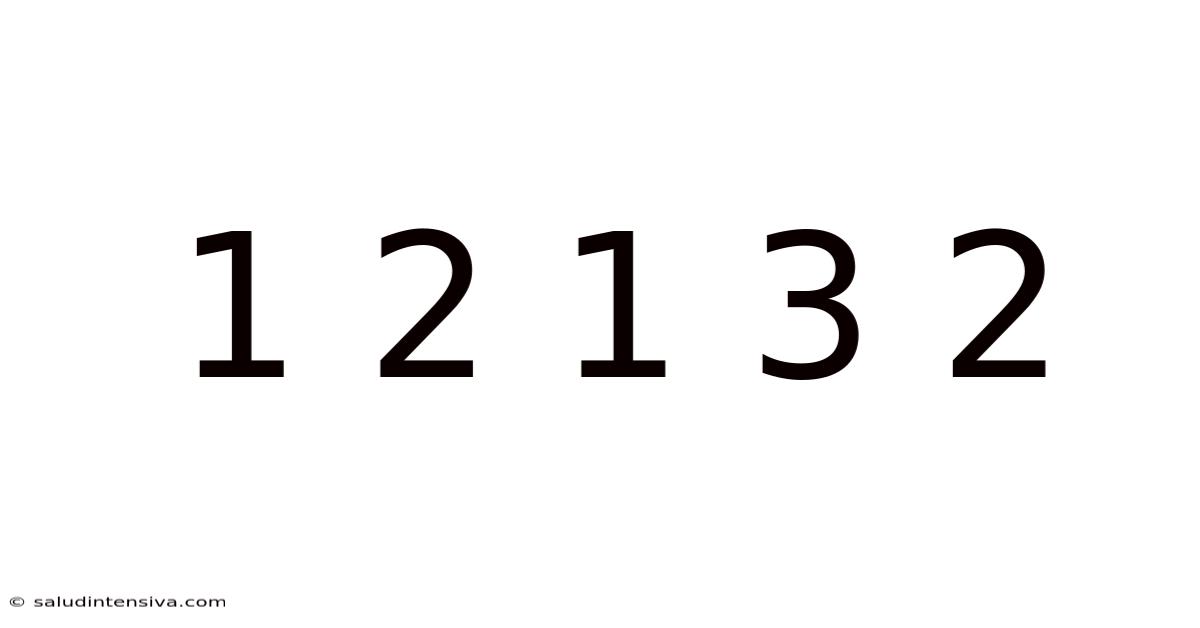
Table of Contents
Decoding the Sequence: Understanding the Mathematical and Pattern Recognition Aspects of 1 2 1 3 2
The seemingly simple sequence "1 2 1 3 2" might appear arbitrary at first glance. However, a deeper dive reveals a rich landscape of potential interpretations, encompassing mathematical analysis, pattern recognition, and even creative problem-solving. This article will explore various perspectives on this sequence, aiming to uncover its underlying structure and potential significance. We'll delve into different approaches to interpreting numerical sequences, highlighting the importance of context and the power of logical deduction. Understanding sequences like this helps hone crucial analytical and problem-solving skills.
Understanding Numerical Sequences: A Foundation
Before we dissect "1 2 1 3 2," it's crucial to understand the general principles of numerical sequences. Sequences are ordered lists of numbers, often following a specific rule or pattern. These patterns can be:
- Arithmetic: Each term is obtained by adding (or subtracting) a constant value to the previous term. Example: 2, 5, 8, 11... (common difference of 3).
- Geometric: Each term is obtained by multiplying (or dividing) the previous term by a constant value. Example: 3, 6, 12, 24... (common ratio of 2).
- Fibonacci-like: Each term is the sum of the two preceding terms. Example: 1, 1, 2, 3, 5, 8...
- Recursive: The next term is defined by a function of previous terms. This is a broad category encompassing many other types of sequences.
- Based on other mathematical operations: Sequences can also be generated using more complex operations like factorial, square root, modulo, etc.
Our sequence, "1 2 1 3 2," doesn't immediately fit into any of these standard categories. This lack of obvious structure is what makes it a fascinating case study for pattern recognition and analytical thinking.
Exploring Potential Interpretations of 1 2 1 3 2
Given the absence of a readily apparent arithmetic or geometric progression, we need to explore more nuanced approaches. Let's consider some possibilities:
1. A Partial Sequence with Missing Context: The most likely explanation is that "1 2 1 3 2" is a snippet of a larger sequence, and without the complete picture, determining the underlying rule becomes challenging. The missing elements could significantly alter our interpretation. This highlights the importance of having complete data when analyzing sequences.
2. A Code or Cipher: The sequence could represent a coded message. This approach requires additional information or a key to decipher its meaning. The numbers might represent letters in an alphabet (e.g., A=1, B=2...), or they could be part of a more complex encryption system. Without further context or a decoding method, this remains speculative.
3. A Representation of a Specific System or Process: The sequence could be a simplified representation of a more complex system or process. For example, it could represent the steps in an algorithm, the stages of a chemical reaction, or the states in a finite state machine. To interpret it in this context, we would need more information about the system it supposedly represents.
4. A Pattern Based on Differences or Ratios: We can examine the differences between consecutive terms:
- 2 - 1 = 1
- 1 - 2 = -1
- 3 - 1 = 2
- 2 - 3 = -1
This doesn't reveal a consistent pattern. Similarly, examining the ratios doesn't provide any clear insight.
5. A Combination of Rules or a Nested Pattern: It's possible that the sequence combines several simple rules, or follows a more complex nested pattern. We might need to look for sub-sequences or repeating motifs within the main sequence to uncover a hidden logic. This requires a more creative and iterative approach to pattern recognition.
6. A Random Sequence: In some cases, a sequence might appear to lack a pattern, but this doesn't necessarily mean it's truly random. Statistical analysis can determine the probability of a sequence being random. However, without a larger dataset, determining the randomness of "1 2 1 3 2" remains inconclusive.
Expanding the Sequence: A Hypothetical Approach
To illustrate the difficulty of interpreting partial sequences, let's try extending the sequence based on different hypothetical rules:
Hypothesis 1: Alternating Addition and Subtraction: If we assume an alternating pattern of adding and subtracting values, we could consider extending it as follows:
1, 2, 1, 3, 2, 4, 1, 5, 2, 6, 1... (Adding 1, then subtracting 1, then adding 2, then subtracting 1, and repeating)
Hypothesis 2: A Recursive Pattern Based on the Previous Two Terms: We could devise a recursive rule. This requires more creativity and intuition and might involve complex functions. There are many possible recursive formulas that could produce the beginning of this sequence. This highlights the non-uniqueness of solutions in such problems.
The Importance of Context and Additional Information
The analysis above clearly demonstrates that without additional context, the interpretation of "1 2 1 3 2" remains ambiguous. To unlock its meaning, we need more information:
- The Source: Where did this sequence originate? Knowing its source could provide crucial clues about its intended meaning.
- The Surroundings: Is it part of a larger dataset, a problem statement, or an instruction set? The surrounding information is often essential to understanding the context.
- The Purpose: What is the intended use of this sequence? Its purpose will influence the appropriate method of interpretation.
Applying Pattern Recognition Techniques
Solving this type of puzzle hinges on strong pattern recognition skills. These are crucial in various fields, including:
- Data Analysis: Identifying trends and anomalies in large datasets.
- Computer Science: Developing algorithms and identifying bugs in code.
- Mathematics: Discovering new mathematical theorems and patterns.
- Cryptography: Breaking codes and ensuring data security.
- Bioinformatics: Analyzing biological sequences like DNA and protein structures.
Developing these skills involves practice, creativity, and a systematic approach. It's often helpful to start with simple patterns and gradually move toward more complex ones.
Frequently Asked Questions (FAQs)
Q: Is there a single definitive answer to the meaning of "1 2 1 3 2"?
A: No. Without more context, there's no single correct interpretation. Multiple plausible explanations exist, each depending on the assumed underlying rule or context.
Q: What mathematical concepts are relevant to understanding sequences like this?
A: Arithmetic and geometric progressions, recursive definitions, Fibonacci sequences, difference equations, and statistical analysis are all relevant concepts.
Q: How can I improve my pattern recognition skills?
A: Practice solving logic puzzles, work with datasets to identify trends, and engage in activities that require finding patterns in data.
Conclusion: The Power of Analytical Thinking
The seemingly simple sequence "1 2 1 3 2" serves as a compelling example of how seemingly random data can conceal underlying structures. Its analysis highlights the importance of context, the limitations of partial information, and the crucial role of analytical thinking and pattern recognition in problem-solving. While we haven't definitively "solved" the sequence, the exploration itself provides valuable insights into the process of interpreting numerical patterns and the development of crucial analytical skills. The quest to uncover the meaning of such sequences encourages creative thinking and reinforces the importance of a systematic and rigorous approach to problem-solving. The ambiguity itself becomes a valuable learning experience, showcasing the diverse range of possibilities and the limitations of incomplete data.
Latest Posts
Latest Posts
-
Inches In A Cubic Yard
Sep 12, 2025
-
1 1 4 3 8
Sep 12, 2025
-
Cm To Square Feet Converter
Sep 12, 2025
-
Multiples Of 3 And 8
Sep 12, 2025
-
What Percentage Is 9 12
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 1 2 1 3 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.