1 2/3 + 1 2/3
saludintensiva
Sep 10, 2025 · 6 min read
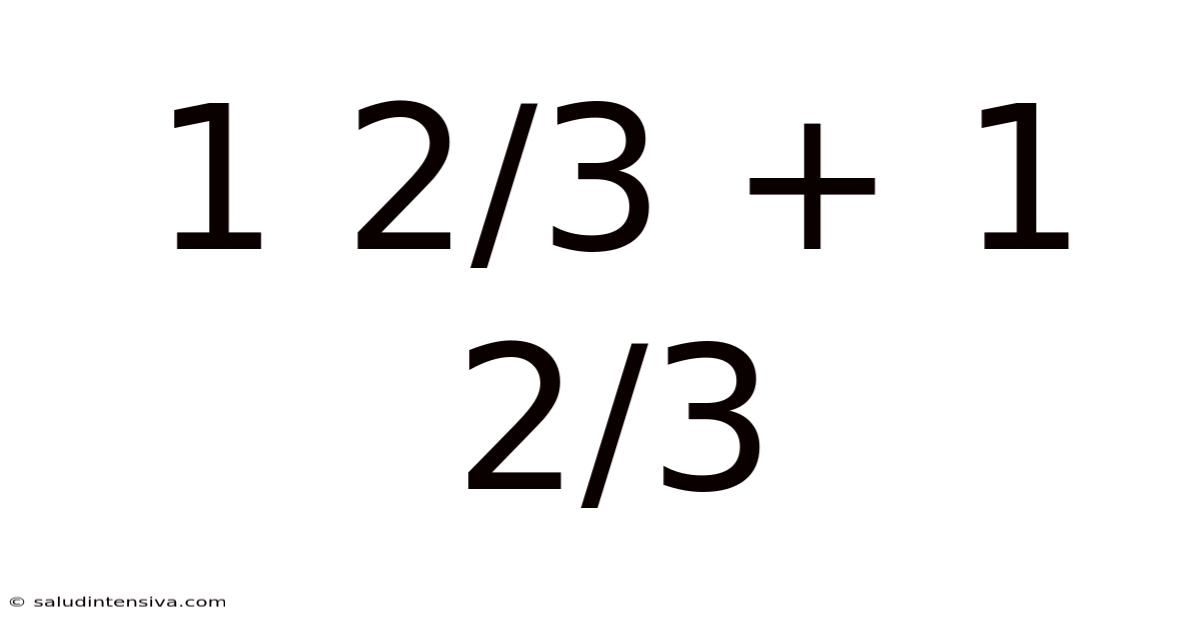
Table of Contents
Decoding the Mystery: A Deep Dive into 1 2/3 + 1 2/3
This article explores the seemingly simple addition problem of 1 2/3 + 1 2/3, going beyond a simple numerical answer to delve into the underlying concepts, different solution methods, and real-world applications. Understanding this seemingly basic operation lays a crucial foundation for more complex mathematical concepts. We'll uncover the magic behind mixed numbers, fractions, and the elegance of mathematical principles. This comprehensive guide is designed for learners of all levels, from those just beginning their mathematical journey to those seeking a deeper understanding of fundamental arithmetic.
Introduction: Understanding Mixed Numbers and Fractions
Before tackling 1 2/3 + 1 2/3, let's refresh our understanding of mixed numbers and fractions. A mixed number combines a whole number and a fraction, like 1 2/3. The '1' represents one whole unit, and the '2/3' represents two parts out of three equal parts of a whole. A fraction, such as 2/3, expresses a part of a whole, with the numerator (2) representing the number of parts and the denominator (3) representing the total number of equal parts that make up the whole.
Method 1: Adding the Whole Numbers and Fractions Separately
This is perhaps the most intuitive method for beginners. We add the whole numbers and the fractions separately, then combine the results.
- Add the whole numbers: 1 + 1 = 2
- Add the fractions: 2/3 + 2/3 = 4/3
Now we have 2 + 4/3. Since 4/3 is an improper fraction (the numerator is larger than the denominator), we convert it to a mixed number. 4 divided by 3 is 1 with a remainder of 1, so 4/3 = 1 1/3.
- Combine the results: 2 + 1 1/3 = 3 1/3
Therefore, 1 2/3 + 1 2/3 = 3 1/3.
Method 2: Converting Mixed Numbers to Improper Fractions
This method offers a more streamlined approach, particularly useful for more complex problems. We convert the mixed numbers into improper fractions before adding them.
-
Convert 1 2/3 to an improper fraction: To do this, multiply the whole number (1) by the denominator (3), add the numerator (2), and place the result over the denominator: (1 x 3) + 2 = 5, so 1 2/3 = 5/3.
-
Convert the second mixed number: Similarly, 1 2/3 = 5/3.
-
Add the improper fractions: 5/3 + 5/3 = 10/3
-
Convert the improper fraction back to a mixed number: 10 divided by 3 is 3 with a remainder of 1, so 10/3 = 3 1/3.
Therefore, 1 2/3 + 1 2/3 = 3 1/3.
Method 3: Visual Representation using Diagrams
A visual approach can enhance understanding, especially for visual learners. We can represent each mixed number using diagrams.
Imagine two circles divided into three equal parts. Each circle represents a whole unit. For 1 2/3, shade one whole circle and two parts of the second circle. Do the same for the second 1 2/3. Counting the shaded parts, we have three whole circles and one part of a circle shaded. This visually confirms our answer: 3 1/3.
The Importance of Common Denominators
In Method 2, we were able to add the fractions directly because they already had a common denominator (3). If we were adding fractions with different denominators, we would need to find a common denominator before adding the numerators. For instance, if we were adding 1/2 + 1/3, we would need to find a common denominator (6) and rewrite the fractions as 3/6 + 2/6 = 5/6.
Real-World Applications: Where do we use this?
Understanding fraction addition is vital in numerous real-world scenarios:
-
Cooking and Baking: Recipes often require fractional measurements. Adding ingredients necessitates understanding fraction addition. For example, if a recipe calls for 1 2/3 cups of flour in one step and another 1 2/3 cups in a later step, knowing how to add these quantities accurately is essential for successful baking.
-
Construction and Measurement: Carpenters, builders, and engineers frequently work with fractional measurements of length, width, and height. Accurate calculations involving fractions are crucial for precise construction. Imagine calculating the total length of two wooden beams, each measuring 1 2/3 meters long.
-
Finance and Budgeting: Dividing a budget or calculating portions of expenses often involves fractions. Understanding fractional arithmetic is crucial for sound financial planning.
-
Sewing and Crafting: Similar to construction, crafting projects often use fractional measurements. Adding lengths of fabric or yarn requires proficiency in fraction addition.
Extending the Concept: More Complex Fraction Problems
The principles applied to 1 2/3 + 1 2/3 can be extended to more complex problems involving various fractions and mixed numbers. The key is to always ensure you have a common denominator before adding the numerators and then simplifying the resulting fraction into its lowest terms or a mixed number if applicable.
Frequently Asked Questions (FAQ)
-
Q: Can I add the whole numbers and fractions in any order? A: While the final answer will be the same, it's generally recommended to add the whole numbers and the fractions separately before combining them for clarity.
-
Q: What if I have fractions with different denominators? A: You must first find the least common denominator (LCD) for those fractions before adding the numerators.
-
Q: Why is converting to improper fractions helpful? A: Converting mixed numbers to improper fractions simplifies the addition process, allowing you to add the fractions directly without dealing with separate whole numbers and fractions.
-
Q: Is there a way to check my answer? A: You can use a calculator to verify your answer, or you can work the problem backward (subtraction) to see if you arrive at the initial numbers. Visual representations also serve as a valuable method to check the answer.
-
Q: What if the problem involved subtracting 1 2/3 from 1 2/3? A: The result would be 0. This is a straightforward example of subtraction, with the concept of finding a common denominator and subtracting numerators, also applicable.
Conclusion: Mastering the Fundamentals
Adding fractions, even seemingly simple problems like 1 2/3 + 1 2/3, is a fundamental skill in mathematics. Mastering this concept provides a solid foundation for more advanced mathematical concepts. By understanding the different methods and their applications, you gain a deeper appreciation for the elegance and practicality of mathematics in our daily lives. Remember to practice regularly, and don't hesitate to explore various methods to find the approach that best suits your learning style. The journey to mathematical mastery is a continuous process of exploration and understanding, and every step, no matter how small, contributes to your overall progress. Continue to explore, question, and delve deeper into the fascinating world of numbers!
Latest Posts
Latest Posts
-
1 2 To The Second Power
Sep 10, 2025
-
Is 3 8 Bigger Than 3 16
Sep 10, 2025
-
Is 3 4 Bigger Than 6 8
Sep 10, 2025
-
25 Degrees C To Kelvin
Sep 10, 2025
-
1 8 Is Greater Than 1 6
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 1 2/3 + 1 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.