1/2 Divided By 3/4 Fraction
saludintensiva
Sep 10, 2025 · 6 min read
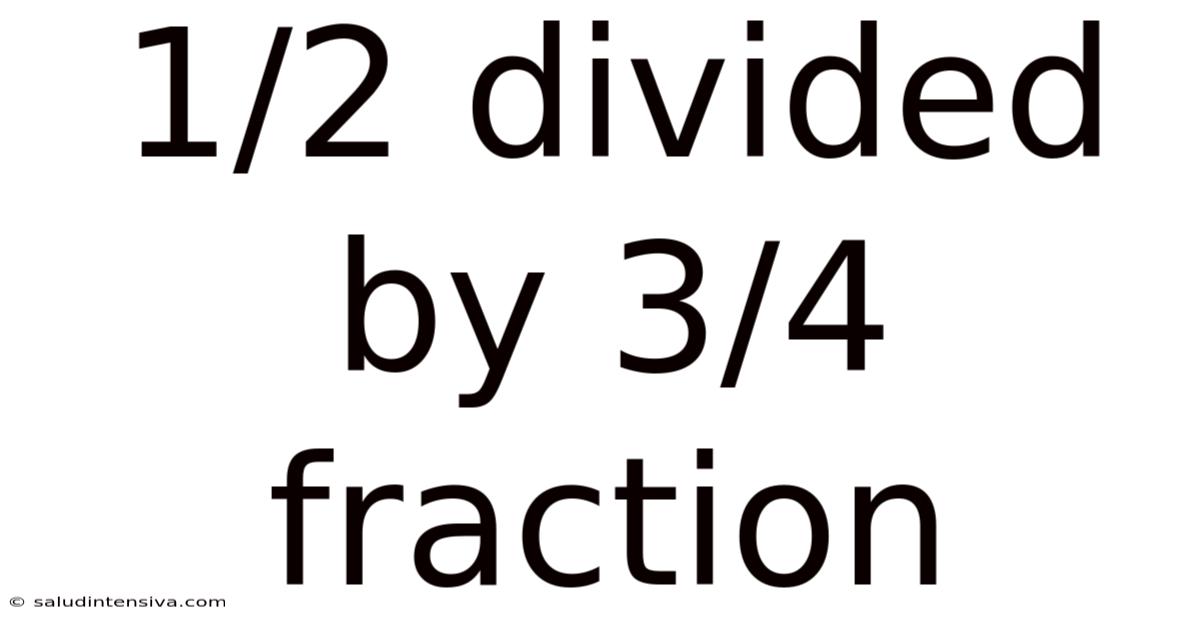
Table of Contents
Understanding 1/2 Divided by 3/4: A Comprehensive Guide
Dividing fractions can seem daunting at first, but with a clear understanding of the process and a bit of practice, it becomes straightforward. This comprehensive guide will walk you through dividing 1/2 by 3/4, explaining the steps involved, the underlying mathematical principles, and providing examples to solidify your understanding. We'll also address common misconceptions and answer frequently asked questions. This guide will equip you with the confidence to tackle any fraction division problem.
Introduction: Why We Divide Fractions
Dividing fractions is a fundamental skill in mathematics with wide-ranging applications in various fields, from cooking and construction to advanced scientific calculations. Understanding how to divide fractions accurately is crucial for solving problems involving ratios, proportions, and more complex mathematical concepts. This article will focus specifically on the division of 1/2 by 3/4, providing a step-by-step explanation and exploring the reasoning behind the method. By the end, you'll not only know how to solve this specific problem but also have a solid grasp of the broader concept of fraction division.
Step-by-Step: Dividing 1/2 by 3/4
The most common and efficient method for dividing fractions involves a simple two-step process:
Step 1: Invert (Reciprocate) the Second Fraction
The key to dividing fractions is to change the division operation into a multiplication operation. To do this, we invert (or find the reciprocal of) the second fraction. The reciprocal of a fraction is obtained by switching the numerator and denominator. In our case, the second fraction is 3/4. Its reciprocal is 4/3.
Step 2: Multiply the First Fraction by the Reciprocal of the Second Fraction
Now that we've inverted the second fraction, we simply multiply the first fraction by the reciprocal. This means we multiply the numerators together and the denominators together.
So, 1/2 divided by 3/4 becomes:
1/2 × 4/3 = (1 × 4) / (2 × 3) = 4/6
Step 3: Simplify the Result (If Necessary)
The final step is to simplify the resulting fraction to its lowest terms. We can simplify 4/6 by finding the greatest common divisor (GCD) of the numerator and denominator. The GCD of 4 and 6 is 2. Dividing both the numerator and denominator by 2, we get:
4/6 = 2/3
Therefore, 1/2 divided by 3/4 equals 2/3.
The Mathematical Reasoning Behind Fraction Division
The method of inverting and multiplying might seem arbitrary at first glance. However, it's rooted in a deeper understanding of what division actually means.
Division can be understood as finding out "how many times" one quantity fits into another. When we divide 1/2 by 3/4, we're essentially asking: "How many times does 3/4 fit into 1/2?"
To visualize this, imagine you have half a pizza (1/2). You want to know how many slices of 3/4 of a pizza you can get from that half pizza. The answer, intuitively, should be less than one whole slice.
Inverting and multiplying allows us to translate this intuitive understanding into a mathematical process. By inverting the second fraction, we are essentially scaling the problem in a way that allows for a straightforward multiplication.
Illustrative Examples
Let's explore a few more examples to reinforce the concept:
-
Example 1: 2/3 divided by 1/6
- Invert the second fraction: 6/1
- Multiply: (2/3) × (6/1) = 12/3
- Simplify: 12/3 = 4
-
Example 2: 5/8 divided by 3/2
- Invert the second fraction: 2/3
- Multiply: (5/8) × (2/3) = 10/24
- Simplify: 10/24 = 5/12
Handling Mixed Numbers
When dealing with mixed numbers (e.g., 1 1/2), you must first convert them into improper fractions before applying the division process.
For example, to divide 1 1/2 by 2/3:
- Convert 1 1/2 to an improper fraction: (1 × 2 + 1) / 2 = 3/2
- Invert the second fraction: 3/2
- Multiply: (3/2) × (3/2) = 9/4
- Convert back to a mixed number (optional): 9/4 = 2 1/4
Dividing Fractions with Whole Numbers
Dividing a fraction by a whole number is also done by inverting and multiplying. Remember, a whole number can be written as a fraction with a denominator of 1.
For example, to divide 1/4 by 2:
- Rewrite 2 as a fraction: 2/1
- Invert the second fraction: 1/2
- Multiply: (1/4) × (1/2) = 1/8
Frequently Asked Questions (FAQ)
Q: Why do we invert the second fraction when dividing fractions?
A: Inverting the second fraction is a mathematical shortcut that effectively transforms the division problem into a multiplication problem. This makes the calculation easier and aligns with the underlying concept of division as finding "how many times" one quantity fits into another.
Q: Can I divide fractions using a different method?
A: While the "invert and multiply" method is the most efficient and commonly used, there are other approaches that might help visualize the process, such as using diagrams or drawing models to represent the fractions involved. However, the "invert and multiply" method remains the most practical for efficient calculation, especially when dealing with more complex fractions.
Q: What if I get a result that isn't in its simplest form?
A: It's always good practice to simplify your final answer to its lowest terms. This ensures clarity and consistency in mathematical representation. You can simplify a fraction by finding the greatest common divisor (GCD) of the numerator and denominator and dividing both by that number.
Q: What if the denominator of the resulting fraction is zero?
A: A denominator of zero is undefined in mathematics. This means there is no solution to the problem. If you encounter this situation, double-check your calculations to ensure there were no errors in the steps.
Q: Are there any online tools to help me check my work?
A: While this article avoids external links, many free online calculators are available that can help you check your fraction division calculations. These tools can provide confirmation of your answers and offer additional practice opportunities.
Q: How can I improve my understanding of fraction division?
A: Practice is key! Work through numerous examples, starting with simple fractions and gradually increasing the complexity. Use visual aids, such as diagrams or real-world examples, to help understand the concept. Additionally, seeking clarification from teachers or tutors can significantly aid your understanding of the subject.
Conclusion: Mastering Fraction Division
Mastering fraction division, especially understanding a problem like 1/2 divided by 3/4, is a crucial step in building a strong mathematical foundation. The "invert and multiply" method, while seemingly simple, offers a powerful and efficient way to solve these problems. By understanding the underlying principles and practicing regularly, you can overcome any initial apprehension and develop the confidence to tackle more challenging fraction problems. Remember the steps, practice consistently, and celebrate your progress as you become proficient in this essential mathematical skill. The ability to confidently divide fractions will open doors to more advanced mathematical concepts and real-world applications, making your learning journey even more rewarding.
Latest Posts
Latest Posts
-
Lcm Of 20 And 24
Sep 10, 2025
-
What Is 2 3 2 3
Sep 10, 2025
-
Illinois Sales Tax Rate Lookup
Sep 10, 2025
-
31 Degree Fahrenheit To Celsius
Sep 10, 2025
-
Convert 21 C To Fahrenheit
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 1/2 Divided By 3/4 Fraction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.