What Is 2/3 + 2/3
saludintensiva
Sep 10, 2025 · 5 min read
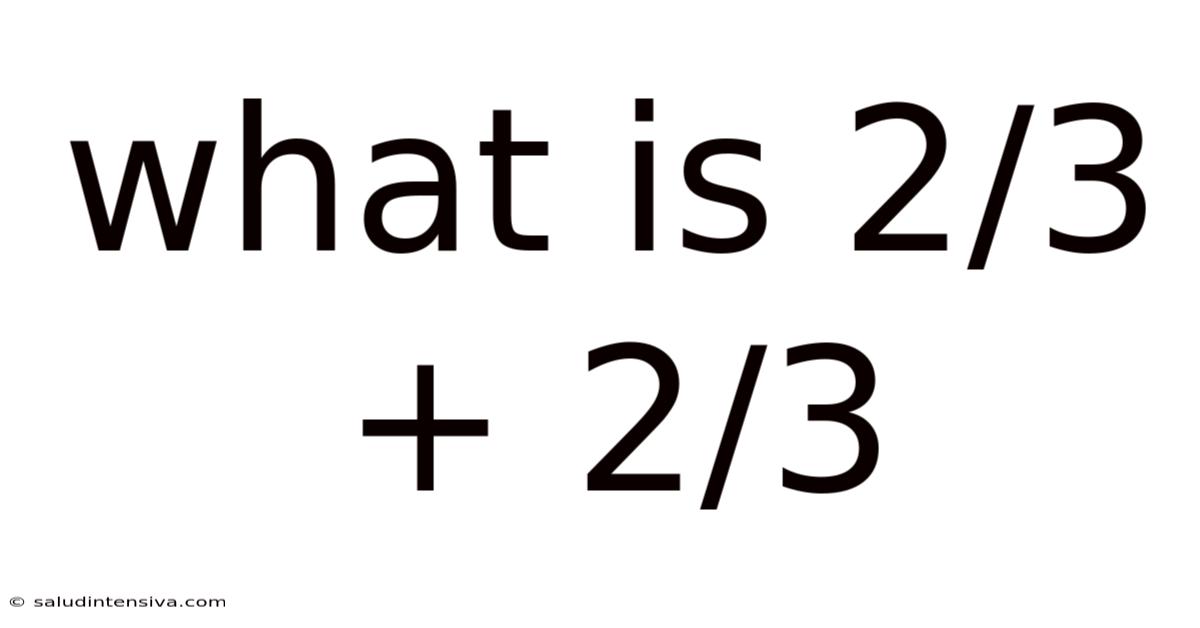
Table of Contents
What is 2/3 + 2/3? A Deep Dive into Fraction Addition
This article explores the seemingly simple addition problem: 2/3 + 2/3. While the answer might seem immediately obvious to some, we will delve into the underlying principles of fraction addition, exploring various methods for solving it, and examining the broader mathematical concepts involved. Understanding this seemingly basic calculation provides a strong foundation for more complex arithmetic and algebraic operations involving fractions. This guide will be particularly beneficial for students learning about fractions, and a helpful refresher for anyone needing to solidify their understanding of this crucial mathematical concept.
Understanding Fractions: A Quick Refresher
Before tackling the addition problem, let's refresh our understanding of fractions. A fraction represents a part of a whole. It is written in the form a/b, where:
- a is the numerator: This represents the number of parts we have.
- b is the denominator: This represents the total number of equal parts the whole is divided into.
For example, in the fraction 2/3, the numerator is 2 (meaning we have 2 parts), and the denominator is 3 (meaning the whole is divided into 3 equal parts). Visualizing this with a pie cut into three slices, 2/3 would represent two of those slices.
Adding Fractions: The Core Principle
The key to adding fractions is ensuring the denominators are the same. This is because we can only directly add parts of the same size. Imagine trying to add two slices of pizza from different sized pizzas – you can't simply add the slices without considering their relative sizes.
If the denominators are already the same, the addition is straightforward: simply add the numerators and keep the denominator unchanged.
Solving 2/3 + 2/3
In our problem, 2/3 + 2/3, the denominators are already identical (both are 3). Therefore, we can directly add the numerators:
2 + 2 = 4
The denominator remains 3. This gives us the answer:
2/3 + 2/3 = 4/3
This is an improper fraction, meaning the numerator (4) is larger than the denominator (3). Improper fractions are perfectly valid, but they are often converted into mixed numbers for easier interpretation.
Converting Improper Fractions to Mixed Numbers
A mixed number combines a whole number and a proper fraction (where the numerator is smaller than the denominator). To convert 4/3 to a mixed number, we perform a division:
4 ÷ 3 = 1 with a remainder of 1
This means 4/3 contains one whole group of 3/3 (which equals 1) and a remainder of 1/3. Therefore:
4/3 = 1 1/3
So, the solution to 2/3 + 2/3 can be expressed as either 4/3 (improper fraction) or 1 1/3 (mixed number). Both are mathematically correct.
Visual Representation
Let's visualize this addition. Imagine two pies, each cut into three equal slices. In the first pie, you take two slices (2/3), and in the second pie, you also take two slices (2/3). Together, you have four slices. Since each pie had three slices, you have 4/3 of a pie, or 1 whole pie and 1/3 of another pie.
Different Methods for Adding Fractions
While the direct method works well when denominators are the same, let's explore other approaches that are useful when dealing with fractions with different denominators.
1. Finding a Common Denominator: If the denominators are different, you must find a common denominator – a number that is a multiple of both denominators. Let's say we want to add 1/2 + 1/3. The least common multiple of 2 and 3 is 6. We then convert each fraction to have a denominator of 6:
1/2 = 3/6 (multiply numerator and denominator by 3) 1/3 = 2/6 (multiply numerator and denominator by 2)
Now we can add: 3/6 + 2/6 = 5/6
2. Using Decimal Equivalents: Fractions can be converted to decimals by dividing the numerator by the denominator. For example, 2/3 ≈ 0.6667. Adding decimals is straightforward: 0.6667 + 0.6667 ≈ 1.3334. This approximates the mixed number 1 1/3. Note that this method might introduce rounding errors, particularly with fractions that result in non-terminating decimals.
The Importance of Understanding Fraction Addition
Mastering fraction addition is crucial for various reasons:
- Foundation for Higher Mathematics: Fraction addition is a fundamental building block for more advanced mathematical concepts, including algebra, calculus, and more.
- Real-World Applications: Fractions are prevalent in daily life – from cooking (measuring ingredients) to finance (dealing with percentages and proportions) to construction (measuring materials).
- Problem-Solving Skills: Solving fraction problems enhances logical reasoning and problem-solving abilities.
- Critical Thinking: Understanding fractions requires a deeper understanding of mathematical principles and how numbers relate to each other.
Frequently Asked Questions (FAQ)
Q: Can you add fractions with different denominators directly?
A: No. You must first find a common denominator before adding the numerators.
Q: What if I get a negative fraction as a result?
A: Negative fractions are valid. They represent parts of a whole in the opposite direction (e.g., a debt instead of a positive asset).
Q: Why is it important to simplify fractions after adding them?
A: Simplifying a fraction reduces it to its lowest terms, making it easier to understand and work with. For example, 6/8 simplifies to 3/4.
Q: Are there any online resources or tools to help with fraction addition?
A: Many educational websites and apps offer interactive exercises and tutorials on fraction addition and other mathematical concepts.
Conclusion
The addition of 2/3 + 2/3, while seemingly simple, provides a valuable opportunity to explore the fundamental concepts of fraction arithmetic. Understanding the principles involved, including finding common denominators and converting between improper fractions and mixed numbers, is crucial for building a solid mathematical foundation. By mastering this basic operation, you pave the way for a deeper understanding of more complex mathematical challenges. Remember to visualize the fractions, use different methods to check your work, and practice regularly to build your confidence and proficiency. The journey to mathematical fluency is built upon mastering these essential building blocks. Keep practicing, and you'll soon find that fractions become much less daunting!
Latest Posts
Latest Posts
-
1 36 As A Decimal
Sep 11, 2025
-
4 1 8 As A Decimal
Sep 11, 2025
-
Convert 33 F To C
Sep 11, 2025
-
Gcf Of 5 And 10
Sep 11, 2025
-
3 4 As A Percent
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about What Is 2/3 + 2/3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.