1 2 Raised To 2
saludintensiva
Sep 19, 2025 · 6 min read
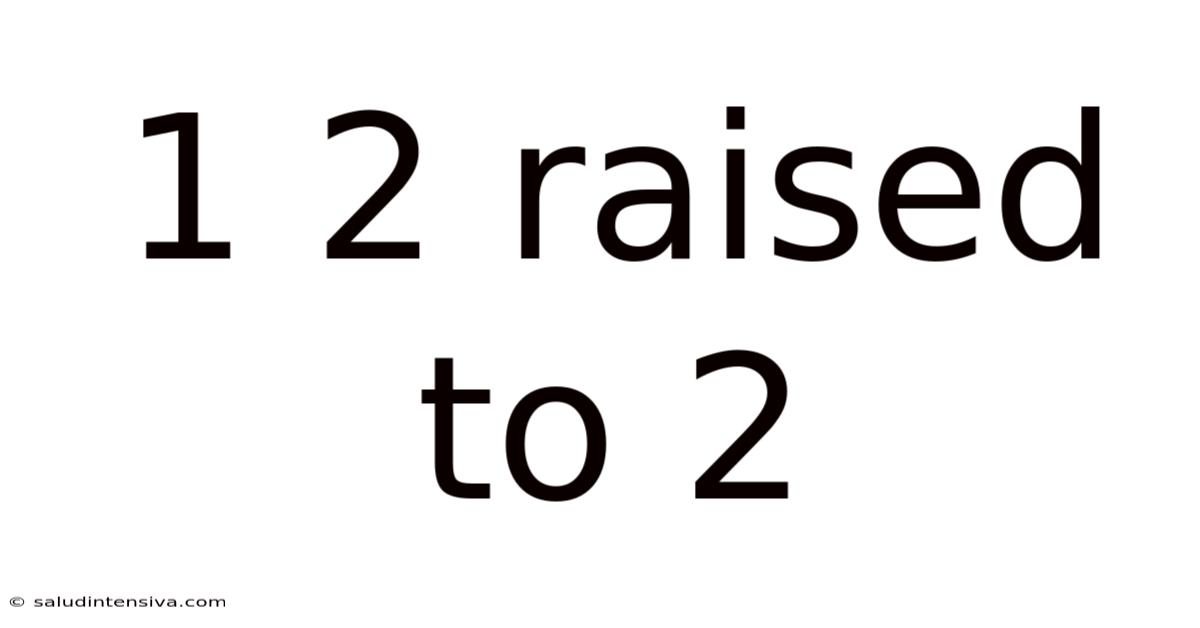
Table of Contents
Decoding 12 Raised to the Power of 2: A Deep Dive into Exponentiation
This article delves into the seemingly simple mathematical expression "12 raised to the power of 2," or 12², exploring its calculation, its significance in various mathematical contexts, and its broader implications in fields beyond pure mathematics. We will unpack the concept of exponentiation, explore different methods of calculating 12², and discuss its applications in geometry, finance, and computer science. Understanding this fundamental concept lays the groundwork for grasping more complex mathematical ideas and real-world applications.
Understanding Exponentiation: Beyond Simple Multiplication
Before we jump into calculating 12², let's first solidify our understanding of exponentiation. Exponentiation, often referred to as "raising to a power," is a mathematical operation involving two numbers: the base and the exponent. The expression b<sup>e</sup> represents the base b raised to the power of the exponent e. It signifies multiplying the base by itself e times.
For example, in 12², 12 is the base and 2 is the exponent. This means we multiply 12 by itself twice: 12 x 12. This is different from simple multiplication, where we'd multiply 12 by a separate number. Exponentiation represents repeated multiplication.
The exponent can be any number – positive integers, negative integers, fractions, even irrational numbers like π (pi). However, in this article, we'll primarily focus on positive integer exponents.
Calculating 12²: Methods and Approaches
Calculating 12² is straightforward, but understanding different approaches enhances our mathematical fluency. Here are a few methods:
-
Direct Multiplication: The most intuitive method is to simply multiply 12 by itself: 12 x 12 = 144. This is the fundamental approach to exponentiation with small, manageable numbers.
-
Using the Distributive Property (for larger numbers): While not strictly necessary for 12², the distributive property becomes crucial when dealing with larger numbers. We can break down the calculation: (10 + 2)² = (10 + 2)(10 + 2) = 10² + 2(10)(2) + 2² = 100 + 40 + 4 = 144. This method expands the expression and uses simpler multiplications.
-
Using a Calculator or Computer: For larger exponents or base numbers, using a calculator or computer software is efficient and reduces the risk of calculation errors. These tools handle complex exponentiation problems quickly and accurately.
-
Visual Representation (Geometric Approach): We can visualize 12² geometrically. Imagine a square with sides of length 12 units. The area of this square represents 12², which is 144 square units. This visualization connects abstract mathematical concepts to tangible geometric representations.
The Significance of 12² in Different Fields
While seemingly a simple calculation, 12² finds applications across various disciplines:
1. Geometry:
-
Area Calculations: As demonstrated earlier, 12² represents the area of a square with 12-unit sides. This is fundamental in calculating areas of more complex shapes that can be divided into squares or rectangles.
-
Volume Calculations: Imagine a cube with 12-unit sides. The volume of this cube is 12³ (12 x 12 x 12 = 1728 cubic units). The concept of 12² lays the foundation for understanding volume calculations in three dimensions.
-
Pythagorean Theorem: The Pythagorean theorem, a cornerstone of geometry, involves squares of side lengths. If you have a right-angled triangle with legs of length 'a' and 'b', and hypotenuse 'c', then a² + b² = c². While 12 itself might not be directly involved, the principle of squaring numbers is central.
2. Algebra and Number Theory:
-
Quadratic Equations: Solving quadratic equations often involves squaring numbers. The term 'x²' frequently appears in these equations, and understanding the concept of squaring is crucial for finding solutions.
-
Number Properties: The properties of perfect squares (numbers that are the square of an integer) are a significant area of study in number theory. 144 (12²) is an example of a perfect square.
3. Finance and Economics:
-
Compound Interest: Compound interest calculations involve exponentiation. The formula A = P(1 + r/n)^(nt) uses exponentiation to determine the future value (A) of an investment with principal (P), interest rate (r), compounding periods (n), and time (t). While 12² might not be directly used, the principle is crucial for understanding the power of compounding over time.
-
Growth Models: Exponential growth models, frequently used in economics and finance, rely on exponentiation to describe phenomena such as population growth, economic expansion, or the spread of infectious diseases.
4. Computer Science:
-
Data Structures and Algorithms: Concepts related to exponentiation are important in analyzing the efficiency of algorithms and data structures. For example, the time complexity of certain algorithms can be expressed using exponential notation.
-
Cryptography: Cryptographic algorithms frequently use exponentiation for tasks such as key generation and encryption/decryption. Large numbers raised to significant powers are integral to many secure communication protocols.
-
Binary Representation: The binary number system (base-2) relies heavily on powers of 2. While 12² doesn’t directly relate, understanding exponentiation is essential to grasp binary arithmetic and data representation in computers.
Expanding Our Understanding: Beyond 12²
While we've focused on 12², the concepts discussed extend far beyond this single calculation. Understanding exponentiation provides a foundation for comprehending:
-
Higher Powers: We can easily extend this to 12³, 12⁴, and so on, exploring the rapid growth that occurs with increasing exponents.
-
Fractional Exponents: Exponentiation also applies to fractional exponents (e.g., 12<sup>1/2</sup>, which is the square root of 12). This opens up the concept of roots and radicals.
-
Negative Exponents: Negative exponents represent reciprocals (e.g., 12<sup>-2</sup> = 1/12²). This introduces the concept of inverse relationships.
-
Complex Exponents: Exponentiation can even involve complex numbers, significantly expanding the scope of its applications in advanced mathematics and physics.
Frequently Asked Questions (FAQ)
Q1: What is the difference between 12 x 2 and 12²?
A1: 12 x 2 is simple multiplication, resulting in 24. 12² (12 raised to the power of 2) is exponentiation, meaning 12 multiplied by itself: 12 x 12 = 144. They represent different mathematical operations.
Q2: How do I calculate 12 raised to a higher power, like 12³?
A2: To calculate 12³, you multiply 12 by itself three times: 12 x 12 x 12 = 1728. Similarly, for any exponent 'n', 12<sup>n</sup> means multiplying 12 by itself 'n' times.
Q3: Are there any real-world examples where 12² is used directly?
A3: While 12² might not always be explicitly stated, the principle of squaring numbers is fundamental in calculating areas of squares with 12-unit sides in construction, design, or any scenario involving area measurement.
Conclusion: The Power of Understanding
The seemingly simple calculation of 12² – equating to 144 – serves as a gateway to a vast world of mathematical concepts and real-world applications. Understanding exponentiation, its methods of calculation, and its significance across various disciplines provides a strong foundation for further mathematical learning and problem-solving. By appreciating the interconnectedness of mathematical principles, we unlock a deeper understanding of the world around us. From the seemingly mundane calculation of 12² to the complexities of advanced mathematical models, the journey of mathematical exploration is both challenging and rewarding.
Latest Posts
Latest Posts
-
Is 11 16 Bigger Than 3 4
Sep 19, 2025
-
How To Find Cubic Polynomial
Sep 19, 2025
-
What Does 1 2 Equal
Sep 19, 2025
-
Sum Of Squares Between Calculator
Sep 19, 2025
-
Gcf Of 16 And 32
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 1 2 Raised To 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.