Is 11/16 Bigger Than 3/4
saludintensiva
Sep 19, 2025 · 5 min read
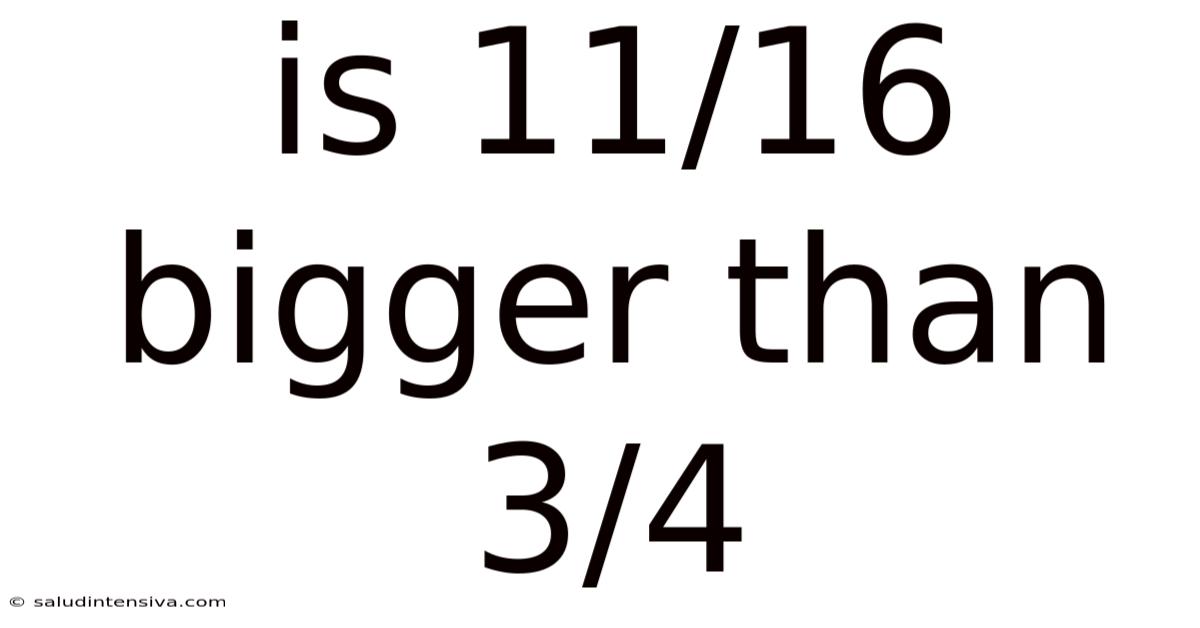
Table of Contents
Is 11/16 Bigger Than 3/4? A Deep Dive into Fraction Comparison
This article will explore the question, "Is 11/16 bigger than 3/4?", providing a comprehensive understanding of fraction comparison techniques. We'll move beyond a simple yes or no answer, delving into the underlying mathematical principles and offering various methods to solve similar problems. Understanding fraction comparison is fundamental in mathematics and has practical applications in various fields. This guide is designed for students of all levels, from those just beginning to understand fractions to those looking to solidify their knowledge.
Introduction to Fractions
Before we tackle the core question, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's expressed as a numerator (the top number) divided by a denominator (the bottom number). The numerator indicates how many parts we have, and the denominator shows how many equal parts the whole is divided into. For example, in the fraction 3/4, the numerator is 3, and the denominator is 4. This means we have 3 out of 4 equal parts.
Method 1: Finding a Common Denominator
The most common and reliable method for comparing fractions is to find a common denominator. This means converting both fractions so they share the same denominator. Once they have the same denominator, we can directly compare the numerators. The fraction with the larger numerator is the larger fraction.
Let's apply this to our problem: Is 11/16 bigger than 3/4?
-
Step 1: Find the least common multiple (LCM) of the denominators. The denominators are 16 and 4. The multiples of 4 are 4, 8, 12, 16, 20... and the multiples of 16 are 16, 32, 48... The least common multiple is 16.
-
Step 2: Convert both fractions to have a denominator of 16. The fraction 11/16 already has a denominator of 16. To convert 3/4, we multiply both the numerator and the denominator by 4: (3 x 4) / (4 x 4) = 12/16.
-
Step 3: Compare the numerators. Now we compare 11/16 and 12/16. Since 12 > 11, we conclude that 12/16 is greater than 11/16.
Therefore, 3/4 (which is equivalent to 12/16) is bigger than 11/16.
Method 2: Converting to Decimals
Another effective method is to convert both fractions into decimals. This allows for easy comparison as decimals are arranged in a straightforward ascending order.
-
Step 1: Convert 11/16 to a decimal. Divide the numerator (11) by the denominator (16): 11 ÷ 16 = 0.6875
-
Step 2: Convert 3/4 to a decimal. Divide the numerator (3) by the denominator (4): 3 ÷ 4 = 0.75
-
Step 3: Compare the decimals. Since 0.75 > 0.6875, we conclude that 3/4 is greater than 11/16.
Method 3: Visual Representation
While less precise for complex fractions, visualizing fractions can be helpful, especially for beginners. Imagine a pie cut into 16 equal slices. 11/16 represents 11 slices. Now imagine a pie cut into 4 equal slices. 3/4 represents 3 slices. If we divide each of the 4 slices into 4 smaller slices, we'd have 16 slices. 3/4 would then represent 12 slices (3 x 4). Clearly, 12 slices are more than 11 slices. This visual representation confirms that 3/4 is larger than 11/16.
Understanding the Mathematical Principles
The success of these methods hinges on the fundamental principle of equivalence in fractions. Multiplying or dividing both the numerator and the denominator by the same non-zero number does not change the value of the fraction. This allows us to manipulate fractions to find a common denominator or convert them to decimals for easier comparison. The concept of least common multiple is crucial for efficient conversion, minimizing unnecessary calculations.
Advanced Techniques: Cross-Multiplication
For comparing two fractions, cross-multiplication offers a more direct approach, avoiding the need to find a common denominator. This method is particularly useful for larger or more complex fractions.
Let's compare 11/16 and 3/4 using cross-multiplication:
-
Step 1: Cross-multiply the numerators and denominators. Multiply the numerator of the first fraction (11) by the denominator of the second fraction (4): 11 x 4 = 44. Then multiply the numerator of the second fraction (3) by the denominator of the first fraction (16): 3 x 16 = 48.
-
Step 2: Compare the products. Since 44 < 48, the fraction with the smaller product (11/16) is the smaller fraction. Therefore, 3/4 is larger.
Practical Applications
The ability to compare fractions is crucial in numerous real-world situations:
- Cooking and Baking: Following recipes often requires understanding fraction measurements.
- Construction and Engineering: Precise measurements using fractions are essential for accuracy and safety.
- Finance and Accounting: Calculating percentages and proportions involves working with fractions.
- Data Analysis: Representing and interpreting data frequently uses fractional representations.
Frequently Asked Questions (FAQ)
-
Q: Can I always use the common denominator method? A: Yes, the common denominator method is a universally applicable method for comparing fractions. While other methods might be quicker in some instances, this method always guarantees an accurate comparison.
-
Q: What if the denominators have no common factors? A: In this case, the least common multiple will simply be the product of the two denominators. For example, comparing 2/5 and 3/7, the LCM is 35.
-
Q: Is it easier to convert fractions to decimals or find a common denominator? A: This depends on personal preference and the specific fractions involved. For simple fractions, decimal conversion might be quicker. For more complex fractions, finding a common denominator might be more efficient and less prone to rounding errors.
-
Q: Are there other ways to compare fractions besides these methods? A: While less common, some individuals utilize visual aids like number lines or fraction bars to compare fractions.
Conclusion: A Comprehensive Understanding of Fraction Comparison
We've explored multiple methods to answer the question, "Is 11/16 bigger than 3/4?", concluding that 3/4 is indeed larger. Beyond simply finding the answer, we've delved into the underlying mathematical principles, demonstrating various techniques to compare fractions effectively. Mastering these methods provides a solid foundation for tackling more complex mathematical problems and applying fractional concepts to various real-world scenarios. Remember, understanding the 'why' behind the 'how' is crucial for developing a deep and lasting comprehension of mathematical concepts. Practice these methods regularly, and you'll confidently navigate the world of fractions.
Latest Posts
Latest Posts
-
Gcf Of 40 And 56
Sep 19, 2025
-
7to The Power Of 2
Sep 19, 2025
-
Definition Of Tip In Math
Sep 19, 2025
-
Excel Hh Mm To Decimal
Sep 19, 2025
-
2 To The Negative 1
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about Is 11/16 Bigger Than 3/4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.