2 To The Negative 1
saludintensiva
Sep 19, 2025 · 5 min read
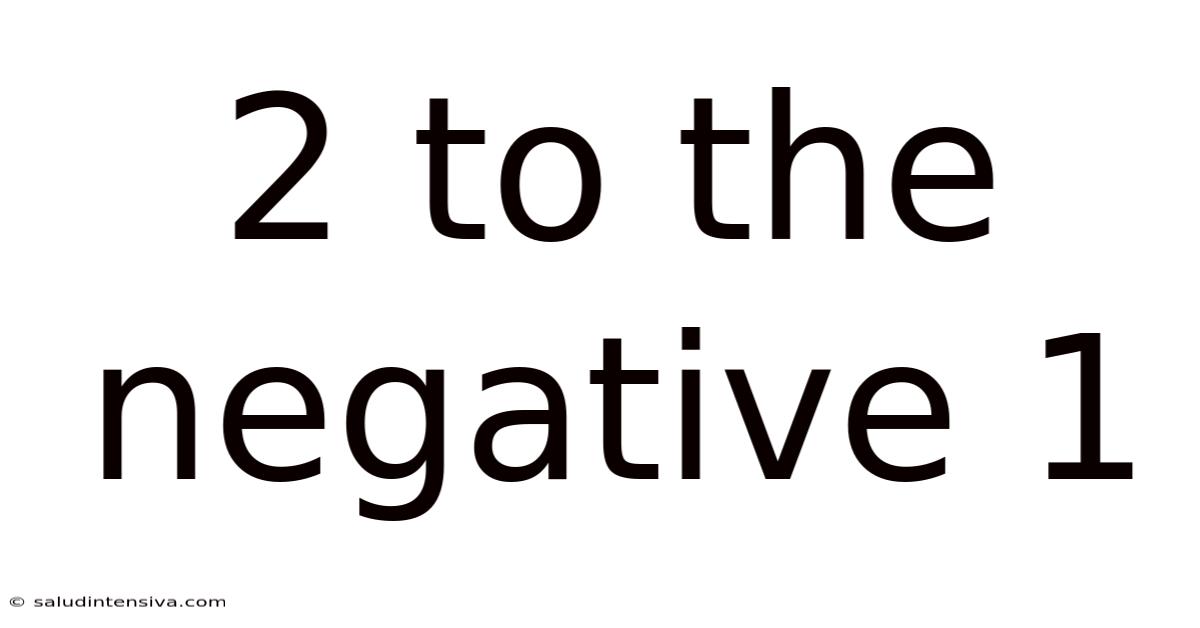
Table of Contents
Understanding 2 to the Negative 1: A Deep Dive into Negative Exponents
This article will explore the concept of 2 to the negative 1 (2⁻¹), demystifying negative exponents and providing a comprehensive understanding of their meaning and application in mathematics. We will cover the fundamental rules, practical examples, and delve into the broader context of exponential functions, ensuring a solid grasp of this crucial mathematical concept. Whether you're a student struggling with exponents or simply seeking a refresher, this guide will equip you with the knowledge to confidently tackle negative exponents.
Introduction to Exponents
Before diving into negative exponents, let's refresh our understanding of positive exponents. An exponent, also known as a power or index, indicates how many times a base number is multiplied by itself. For example:
- 2³ = 2 × 2 × 2 = 8 (2 raised to the power of 3)
- 5² = 5 × 5 = 25 (5 raised to the power of 2)
- 10⁴ = 10 × 10 × 10 × 10 = 10,000 (10 raised to the power of 4)
The base number is the number being multiplied, and the exponent tells us how many times to perform the multiplication.
Understanding Negative Exponents
Negative exponents might seem daunting at first, but they follow a consistent and logical rule. The key is to understand that a negative exponent does not imply a negative result. Instead, it signifies a reciprocal operation. Specifically:
a⁻ⁿ = 1/aⁿ
This means that a number raised to a negative exponent is equal to 1 divided by that number raised to the positive exponent.
Let's apply this rule to our example: 2⁻¹
2⁻¹ = 1/2¹ = 1/2 = 0.5
Therefore, 2 to the negative 1 is equal to 1/2, or 0.5. This is a fundamental concept that forms the basis for understanding more complex exponential expressions.
Step-by-Step Explanation of 2⁻¹
To further clarify, let's break down the calculation of 2⁻¹ step-by-step:
-
Identify the base and exponent: In the expression 2⁻¹, the base is 2, and the exponent is -1.
-
Apply the rule for negative exponents: According to the rule, a⁻ⁿ = 1/aⁿ, we rewrite 2⁻¹ as 1/2¹.
-
Simplify the expression: 2¹ is simply 2. Therefore, 1/2¹ simplifies to 1/2.
-
Convert to decimal (optional): The fraction 1/2 can be easily converted to its decimal equivalent, 0.5.
Practical Applications of Negative Exponents
Negative exponents are not merely abstract mathematical concepts; they have widespread applications in various fields, including:
-
Science: Negative exponents are frequently used in scientific notation to represent very small numbers. For instance, the speed of light is approximately 3 x 10⁸ meters per second, while the charge of an electron is approximately 1.6 x 10⁻¹⁹ coulombs.
-
Engineering: In engineering calculations, negative exponents are used to express very small quantities or to represent inverse relationships.
-
Finance: Compound interest calculations often involve negative exponents when dealing with present values and future values of investments.
-
Computer Science: Negative exponents are crucial in representing floating-point numbers and performing binary calculations.
Expanding the Concept: Beyond 2⁻¹
While we've focused on 2⁻¹, the rule for negative exponents applies to any base number. Let's look at a few more examples:
-
3⁻² = 1/3² = 1/9 ≈ 0.111
-
10⁻³ = 1/10³ = 1/1000 = 0.001
-
(1/2)⁻¹ = 1/(1/2) = 2 Notice how a negative exponent applied to a fraction inverts the fraction.
The Scientific Notation Connection
Negative exponents are particularly useful in scientific notation, a way to express very large or very small numbers concisely. Scientific notation uses the form a x 10ⁿ, where 'a' is a number between 1 and 10, and 'n' is an integer exponent. A negative exponent in scientific notation indicates a very small number. For example:
- 0.0000000001 can be expressed as 1 x 10⁻¹⁰
Negative Exponents and Exponential Functions
Negative exponents are integral to the concept of exponential functions. An exponential function has the general form f(x) = aˣ, where 'a' is the base and 'x' is the exponent. When x is negative, the function represents the reciprocal of the positive exponential function. These functions are used to model various phenomena, such as population growth, radioactive decay, and compound interest.
Frequently Asked Questions (FAQ)
Q: Can a base number be negative when using negative exponents?
A: Yes, a base number can be negative. However, you need to be careful with the order of operations and consider the rules for even and odd exponents when dealing with negative bases. For example, (-2)² = 4, while (-2)³ = -8. The same principles apply when using negative exponents.
Q: What is 0⁻¹?
A: 0⁻¹ is undefined. Division by zero is not allowed in mathematics.
Q: How do I calculate 2⁻¹ using a calculator?
A: Most calculators will handle negative exponents directly. You would typically enter 2, then the exponent button (usually denoted as ^, xʸ, or yˣ), then -1, and finally the equals sign (=).
Q: Why are negative exponents important?
A: Negative exponents provide a concise and efficient way to represent very small numbers, are fundamental to understanding exponential functions and their applications, and are crucial for various scientific and engineering calculations.
Conclusion
Understanding negative exponents, especially 2⁻¹, is a crucial stepping stone in mastering more advanced mathematical concepts. By applying the simple rule a⁻ⁿ = 1/aⁿ and understanding its implications, you can confidently tackle problems involving negative exponents and appreciate their practical applications across diverse fields. Remember the key takeaway: a negative exponent doesn't result in a negative number, but rather indicates a reciprocal. This understanding will serve you well as you continue your mathematical journey. From scientific notation to exponential functions, the power of the negative exponent is undeniable and far-reaching.
Latest Posts
Latest Posts
-
What Is 6 5 Simplified
Sep 19, 2025
-
1 3 X 1 6
Sep 19, 2025
-
Lcm Of 8 And 4
Sep 19, 2025
-
10 Out Of 15 Percent
Sep 19, 2025
-
How Long Is 340 Minutes
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about 2 To The Negative 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.