1 3 2 2 3
saludintensiva
Sep 17, 2025 · 6 min read
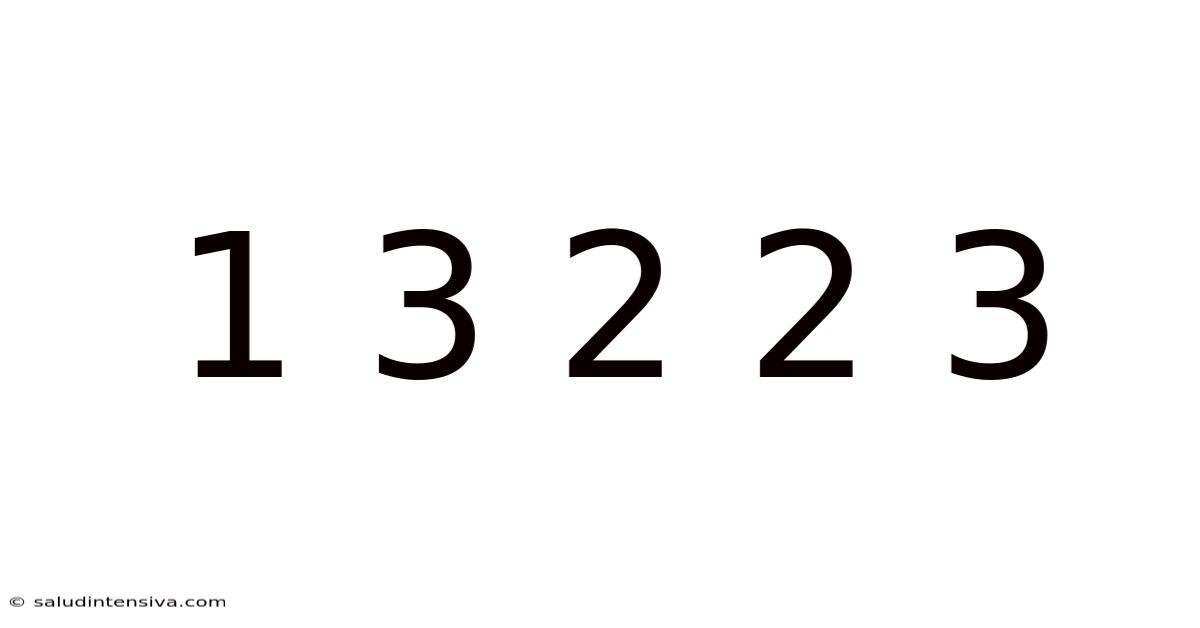
Table of Contents
Decoding the Mystery: Unveiling the Significance of the Sequence 1 3 2 2 3
The seemingly simple sequence "1 3 2 2 3" might initially appear arbitrary. However, depending on the context, this sequence could represent a code, a pattern in nature, or even a solution to a mathematical problem. This article delves deep into the potential interpretations and meanings behind this numeric sequence, exploring its possibilities across various disciplines and prompting a deeper understanding of pattern recognition and problem-solving. We will examine potential mathematical interpretations, explore connections to existing number sequences, discuss possibilities in coding and cryptography, and finally, contemplate its potential relevance in fields like music and art.
I. Mathematical Interpretations and Number Theory
At first glance, 1 3 2 2 3 doesn't immediately align with well-known mathematical sequences like Fibonacci or Lucas numbers. However, let's explore some potential mathematical interpretations:
-
Prime Factorization and Divisibility: We can analyze the individual numbers for prime factors. 1 is neither prime nor composite; 3 is prime; 2 is prime; and again, 2 is prime. The number 3 is also prime. This analysis doesn't immediately reveal a clear pattern, but understanding the prime factorization of each number might be a starting point for further exploration, particularly if additional numbers were added to the sequence. We could investigate whether the sequence might relate to the number of prime factors for each number or some function of their prime factorizations.
-
Modular Arithmetic: Exploring modular arithmetic, where numbers "wrap around" after reaching a certain modulus, is another avenue. For example, considering the sequence modulo 3 (the remainder when divided by 3), we get 1, 0, 2, 2, 0. This pattern doesn't immediately suggest a clear mathematical rule. Experimenting with different moduli might uncover hidden relationships.
-
Difference Sequences: We can calculate the differences between consecutive numbers: 3 - 1 = 2, 2 - 3 = -1, 2 - 2 = 0, 3 - 2 = 1. The resulting sequence (2, -1, 0, 1) is still irregular. However, analyzing the second differences (differences between the differences) might reveal hidden patterns. Applying this method iteratively might uncover a structure hidden within the apparent randomness.
-
Relationship to Existing Number Sequences: While it doesn't directly match known sequences, the sequence could be a subsequence of a larger, more complex sequence. This possibility necessitates the need for additional data points to identify potential underlying rules or generative functions.
II. Coding and Cryptography Implications
The sequence "1 3 2 2 3" could represent a simplified code or part of a more complex cryptographic system. In cryptography, short sequences are often used as keys, identifiers, or parts of larger encryption algorithms.
-
Substitution Cipher: The sequence could represent a simple substitution cipher, where each number maps to a letter or symbol. However, without a key or more context, deciphering this is impossible. For example, 1 could map to 'A', 3 to 'C', 2 to 'B', resulting in the sequence 'ACBBC'. However, this is pure speculation without additional information.
-
Part of a Larger Key: It is more likely that such a short sequence serves as a component within a more extensive key or encryption algorithm. In this case, it would be meaningless in isolation but crucial in the broader context of the cryptographic system.
-
Index or Pointer: The numbers could represent indices or pointers within a data structure or array. Their meaning would then depend entirely on the context of the data they are referencing.
III. Exploring Potential Connections in Music and Art
While less directly apparent, the sequence could have potential applications in musical composition or artistic design.
-
Musical Rhythms and Meter: The numbers could represent durations of notes or rests within a musical phrase. For instance, 1 could represent a quarter note, 3 a dotted quarter note, 2 an eighth note, etc. Experimenting with various interpretations could lead to interesting musical explorations.
-
Visual Art and Pattern Generation: The sequence might be used as a base for generating patterns in visual arts. Imagine using the sequence to determine the size, position, or color of elements in a painting or a digital artwork. Repeated iterations and variations of the sequence could create complex and visually appealing designs.
-
Generating Fractal Patterns: Sequences are frequently used in the generation of fractal patterns. While the sequence "1 3 2 2 3" itself might not directly generate a recognizable fractal, it could be incorporated as part of a more complex iterative function for fractal generation.
IV. Step-by-Step Analysis and Problem-Solving Approaches
Let's approach the sequence systematically, attempting to identify underlying patterns or relationships. This involves a methodical investigation across multiple domains:
-
Data Expansion: The most significant limitation is the brevity of the sequence. Obtaining additional numbers would provide crucial context. Without more data, any conclusions drawn are purely speculative.
-
Contextual Analysis: The meaning of the sequence is highly dependent on the context in which it was presented. Understanding the source and any accompanying information would help in interpretation.
-
Pattern Recognition Techniques: Employing various pattern recognition techniques, including those mentioned earlier (difference sequences, modular arithmetic), would be crucial in unveiling hidden structure.
-
Computational Approaches: Using computer programs to search for patterns or analyze the sequence in different mathematical spaces could reveal hidden relationships. This might involve searching for similarities to known mathematical sequences or generating potential extensions of the sequence based on various algorithms.
-
Cross-Disciplinary Thinking: Combining approaches from different fields, like mathematics, cryptography, music theory, and visual arts, offers the best chance of successfully deciphering the sequence.
V. Frequently Asked Questions (FAQ)
Q: Is there a definitive answer to what "1 3 2 2 3" means?
A: No. Without additional information or context, the sequence remains ambiguous. The possibilities explored above represent only potential interpretations.
Q: Could this be a simple counting sequence with errors?
A: It's possible, but unlikely. The irregularity of the sequence makes a simple counting error less plausible.
Q: What's the importance of investigating seemingly random sequences?
A: Investigating such sequences helps develop critical thinking, problem-solving skills, and a deeper understanding of pattern recognition across various disciplines. It showcases how the same sequence can have multiple interpretations depending on context.
Q: Where can I find more information about this specific sequence?
A: This sequence isn't widely documented in literature. The lack of publicly available information highlights its ambiguity and the need for more context.
VI. Conclusion
The sequence "1 3 2 2 3" presents a fascinating challenge in pattern recognition and problem-solving. While it doesn't directly correlate with established mathematical sequences or cryptographic techniques without further context, its potential interpretations span multiple fields. This analysis emphasizes the importance of considering various perspectives and employing diverse problem-solving strategies. The brevity of the sequence limits definitive conclusions; however, this exploration serves as a valuable exercise in analytical thinking and highlights the power of interdisciplinary approaches to problem-solving. Further investigation, particularly with additional data points and contextual information, is necessary to unlock the true meaning of this enigmatic sequence. The journey of exploration itself, however, offers significant insights into the processes of pattern recognition and creative problem-solving.
Latest Posts
Latest Posts
-
Is 1 6 Greater Than 1 2
Sep 17, 2025
-
Cube Root In Fraction Form
Sep 17, 2025
-
Whats 3 Percent Of 100
Sep 17, 2025
-
20 9 As A Mixed Number
Sep 17, 2025
-
160 M2 To Square Feet
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 1 3 2 2 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.