Is 1/6 Greater Than 1/2
saludintensiva
Sep 17, 2025 · 5 min read
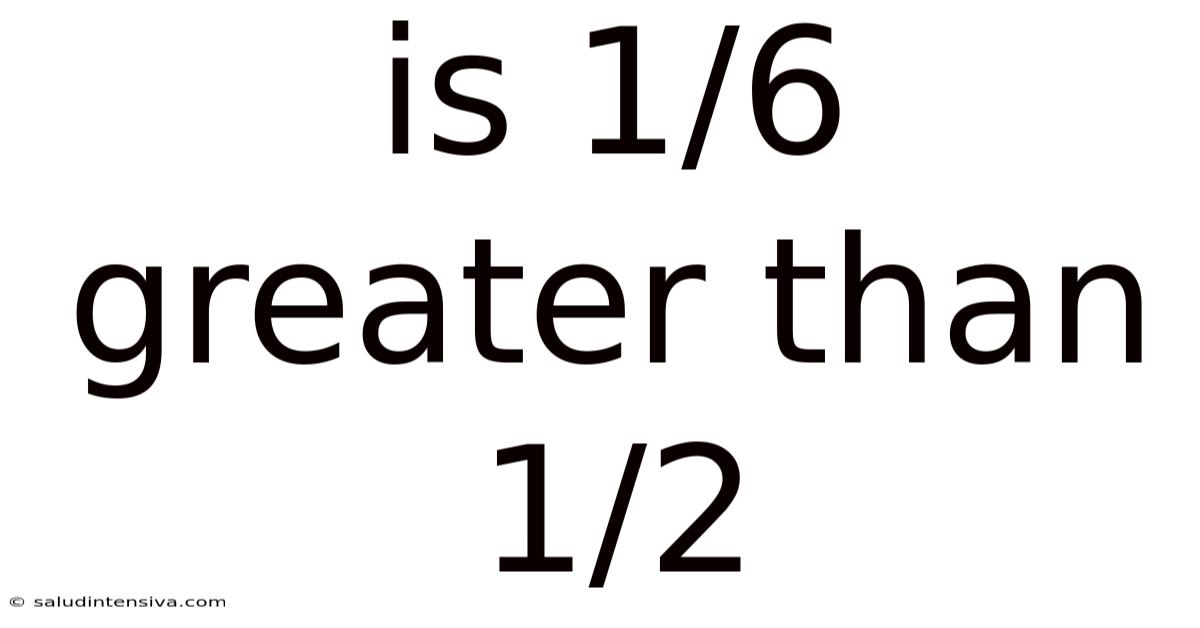
Table of Contents
Is 1/6 Greater Than 1/2? Understanding Fractions and Comparisons
Understanding fractions is a fundamental concept in mathematics, crucial for various applications in everyday life and advanced studies. This article aims to comprehensively address the question: "Is 1/6 greater than 1/2?" We'll explore the concept of fractions, methods for comparing them, and delve into the reasoning behind the answer, providing a clear and intuitive understanding for learners of all levels. This will include practical examples and address frequently asked questions, ensuring a thorough grasp of this essential mathematical skill.
Introduction to Fractions
A fraction represents a part of a whole. It's written as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator indicates how many of those parts are being considered. For example, in the fraction 1/2, the whole is divided into two equal parts, and we are considering one of those parts.
Visualizing Fractions: A Pictorial Approach
Visual aids are extremely helpful in understanding fractions. Imagine a pizza cut into six equal slices. 1/6 represents one slice of that pizza. Now, imagine a different pizza cut into only two equal slices. 1/2 represents one of those two slices. By comparing the sizes of these slices visually, it becomes immediately clear that one half (1/2) of the pizza is considerably larger than one-sixth (1/6) of the pizza. This visual representation makes the comparison intuitive and easy to grasp.
Comparing Fractions: Different Methods
There are several methods for comparing fractions. Let's examine the most common approaches:
-
Visual Comparison: As illustrated with the pizza example, visualizing fractions can be effective, particularly for simpler fractions. However, this method becomes less practical when dealing with more complex fractions.
-
Common Denominator Method: This is the most reliable method for comparing fractions. The process involves finding a common denominator – a number that is a multiple of both denominators. Once you have a common denominator, you can directly compare the numerators. The fraction with the larger numerator is the larger fraction.
Let's apply this method to compare 1/6 and 1/2:
-
Find a common denominator: The least common multiple (LCM) of 6 and 2 is 6.
-
Convert the fractions:
- 1/2 remains 1/2 since its denominator is already 6.
- To convert 1/2 to have a denominator of 6, we multiply both the numerator and the denominator by 3: (1 x 3) / (2 x 3) = 3/6
-
Compare the numerators: Now we compare 1/6 and 3/6. Since 3 > 1, 3/6 (which is equivalent to 1/2) is greater than 1/6.
-
Decimal Conversion Method: Another approach is to convert the fractions to decimals. This can be done by dividing the numerator by the denominator.
- 1/6 = 0.1666...
- 1/2 = 0.5
Comparing the decimal values, 0.5 is clearly greater than 0.1666... Therefore, 1/2 > 1/6.
Is 1/6 Greater Than 1/2? The Definitive Answer
Based on the methods outlined above – visual comparison, common denominator method, and decimal conversion – the answer is a resounding no. 1/6 is not greater than 1/2. In fact, 1/2 is significantly larger than 1/6.
Understanding the Relationship Between Numerator and Denominator
The size of a fraction is directly influenced by the relationship between its numerator and denominator. A larger numerator, relative to the denominator, results in a larger fraction. Conversely, a smaller numerator, relative to the denominator, results in a smaller fraction. In the case of 1/6 and 1/2, the denominator of 2 in 1/2 is much smaller than the denominator of 6 in 1/6, making the fraction 1/2 inherently larger.
Real-World Applications: Fractions in Everyday Life
Understanding fractions is vital in many aspects of daily life:
-
Cooking and Baking: Recipes often use fractions to specify ingredient amounts.
-
Measurement: Measuring tools like rulers and measuring cups utilize fractions (e.g., 1/4 inch, 1/2 cup).
-
Sharing and Division: Dividing resources fairly among individuals often involves fractions.
-
Finance: Understanding percentages and proportions – which are essentially fractions – is crucial for managing finances.
Frequently Asked Questions (FAQs)
-
Q: Why is the common denominator method the most reliable?
- A: Because it allows for a direct comparison of the numerators once the fractions have been standardized to have the same denominator. Visual comparison can be subjective and decimal conversion might lead to rounding errors.
-
Q: Are there other ways to compare fractions?
- A: Yes, there are more advanced methods, such as cross-multiplication, that become more useful when comparing fractions with different denominators.
-
Q: What if the fractions have a common numerator?
- A: If two fractions have the same numerator, the fraction with the smaller denominator is the larger fraction.
-
Q: How can I improve my understanding of fractions?
- A: Practice is key. Work through various problems, use visual aids, and try different comparison methods. Online resources and educational apps can also be very helpful.
Conclusion: Mastering Fractions for Future Success
Mastering fractions is a cornerstone of mathematical literacy. By understanding the concepts of numerator, denominator, and different comparison methods, you can confidently tackle fraction-based problems. The comparison of 1/6 and 1/2, seemingly simple, serves as a foundation for understanding more complex fractional relationships. Continuous practice and application of these concepts will build confidence and proficiency in this crucial mathematical area, opening doors to more advanced mathematical concepts and real-world applications. Remember, consistent effort and a patient approach are key to mastering fractions and unlocking their practical value.
Latest Posts
Latest Posts
-
27 Out Of 30 Percent
Sep 17, 2025
-
Gcf Of 72 And 24
Sep 17, 2025
-
4 Divided By Negative 2
Sep 17, 2025
-
3 5 Simplified As A Fraction
Sep 17, 2025
-
1 2 Minus 1 4
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Is 1/6 Greater Than 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.