1 6 Divided By 7
saludintensiva
Sep 21, 2025 · 5 min read
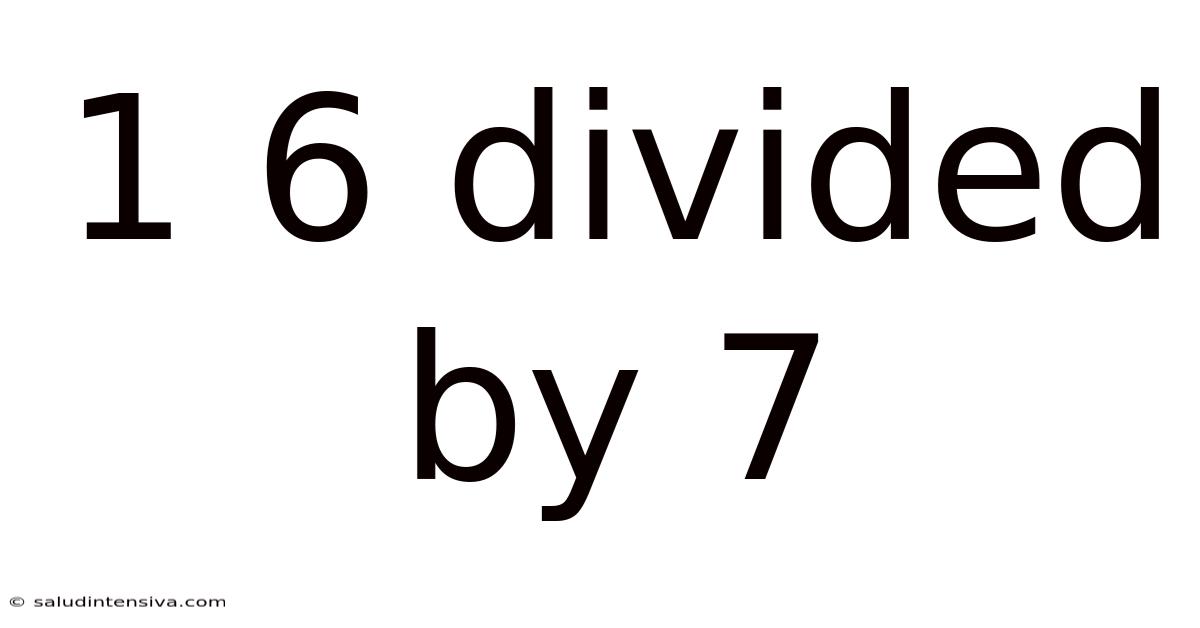
Table of Contents
Exploring the Division: 16 Divided by 7
Understanding division is a fundamental concept in mathematics, forming the bedrock for more complex calculations and problem-solving. This article delves into the seemingly simple problem of 16 divided by 7, exploring various approaches to solve it, explaining the underlying mathematical principles, and offering a deeper understanding of the concepts involved. We will move beyond simply stating the answer and explore the "why" behind the solution, making this a valuable resource for students and anyone looking to refresh their mathematical knowledge.
Understanding Division: A Quick Recap
Division is essentially the process of splitting a quantity into equal parts. When we say "16 divided by 7," we're asking how many times 7 fits into 16, and what portion remains if it doesn't fit perfectly. This leads us to two key components of division: the quotient (the whole number of times the divisor goes into the dividend) and the remainder (the amount left over).
In the context of 16 divided by 7:
- Dividend: 16 (the number being divided)
- Divisor: 7 (the number we're dividing by)
- Quotient: This is what we need to find.
- Remainder: This is also what we need to find.
Solving 16 Divided by 7: Step-by-Step
We can solve this using long division, a method familiar to most students.
-
Set up the long division: Write 16 inside the long division symbol (⟌) and 7 outside.
7⟌16 -
Determine how many times 7 goes into 16: 7 goes into 16 two times (7 x 2 = 14). This is our quotient.
-
Multiply and subtract: Multiply the quotient (2) by the divisor (7): 2 x 7 = 14. Subtract this result from the dividend (16): 16 - 14 = 2. This is our remainder.
-
Write the answer: The answer is expressed as a quotient with a remainder: 2 remainder 2, or 2 R 2. This means 7 goes into 16 two times with 2 left over.
2 R 2 7⟌16 -14 --- 2
Representing the Solution: Fractions and Decimals
While the whole number quotient and remainder provide a clear understanding, we can also express the solution as a fraction or a decimal.
-
Fraction: The remainder (2) becomes the numerator, and the divisor (7) becomes the denominator: 2/7. Therefore, 16 divided by 7 can be represented as 2 2/7 (a mixed number – a whole number and a fraction). This form accurately reflects the whole number of times 7 goes into 16 and the fractional part remaining.
-
Decimal: To convert the fraction 2/7 to a decimal, we perform long division again:
0.2857... 7⟌2.0000 -14 --- 60 -56 --- 40 -35 --- 50 -49 --- 10 ...
As you can see, the decimal representation (0.2857...) is a non-terminating, repeating decimal. This means the digits continue infinitely. We often round the decimal to a certain number of decimal places for practical use (e.g., 2.29, rounded to two decimal places). This highlights that while decimals are useful, they sometimes lead to approximations, unlike the fraction which maintains precision.
The Importance of Remainders
Remainders are not simply "leftovers"; they hold significant mathematical importance. They represent the portion of the dividend that cannot be evenly divided by the divisor. This is crucial in many real-world applications:
-
Sharing: If you have 16 cookies and want to share them equally among 7 friends, each friend gets 2 cookies (the quotient), and you have 2 cookies left over (the remainder).
-
Measurement: If you have a 16-meter rope and need to cut it into 7-meter lengths, you can cut two 7-meter lengths (the quotient), leaving 2 meters of rope (the remainder).
-
Programming: Remainders are fundamental in computer programming, used in operations like modulo arithmetic (% operator in many programming languages) to determine if a number is even or odd, or for various other cyclical operations.
Exploring Deeper Mathematical Concepts
This seemingly simple division problem opens doors to several more advanced mathematical concepts:
-
Modular Arithmetic: As mentioned, the remainder plays a vital role in modular arithmetic. In this system, we are only concerned with the remainder after division by a specific modulus (in our case, 7). This is frequently used in cryptography, number theory, and computer science.
-
Rational Numbers: The fraction 2/7 represents a rational number, a number that can be expressed as a ratio of two integers. Understanding rational numbers is essential for working with fractions, decimals, and proportions.
-
Real Numbers: The decimal representation of 2/7, though non-terminating, is a real number, belonging to a broader set of numbers encompassing both rational and irrational numbers (like π and √2).
-
Approximation and Error: When we round the decimal representation of 2/7, we introduce an error or approximation. Understanding how to manage and minimize errors is crucial in scientific calculations and engineering.
Frequently Asked Questions (FAQ)
Q: What is the most accurate way to represent the answer to 16 divided by 7?
A: The most accurate representation is the mixed number 2 2/7. It captures the whole number quotient and the precise fractional remainder. Decimals, while convenient, often require rounding and introduce approximations.
Q: Why is the decimal representation of 2/7 a repeating decimal?
A: A decimal representation is repeating when the denominator of the fraction (in this case, 7) contains prime factors other than 2 and 5. Since 7 is a prime number not equal to 2 or 5, its decimal representation will repeat.
Q: Are there other ways to solve 16 divided by 7 besides long division?
A: Yes. You can use a calculator, although understanding the process of long division provides a deeper understanding of the mathematical principles. You can also visualize it using objects or diagrams to physically divide 16 items into 7 groups.
Conclusion
The seemingly simple problem of 16 divided by 7 provides a rich exploration into fundamental mathematical concepts. It's not just about finding the answer; it's about understanding the nuances of division, interpreting remainders, and appreciating the various ways we can represent the solution. Whether expressing the answer as a mixed number, a fraction, or a decimal, each representation offers unique insights and serves different purposes. This exploration hopefully provides a deeper understanding of the fundamental arithmetic operation of division and highlights its connections to more advanced mathematical concepts. Remember, the journey of learning mathematics is not just about memorizing procedures but about grasping the underlying principles and applying them creatively.
Latest Posts
Latest Posts
-
80 Degrees F To Celsius
Sep 21, 2025
-
X 5 X 7 Simplify
Sep 21, 2025
-
How To Form A Curb
Sep 21, 2025
-
Convert 24 Yards To Feet
Sep 21, 2025
-
Whats 90 Degrees In Celsius
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about 1 6 Divided By 7 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.