X 5 X 7 Simplify
saludintensiva
Sep 21, 2025 · 6 min read
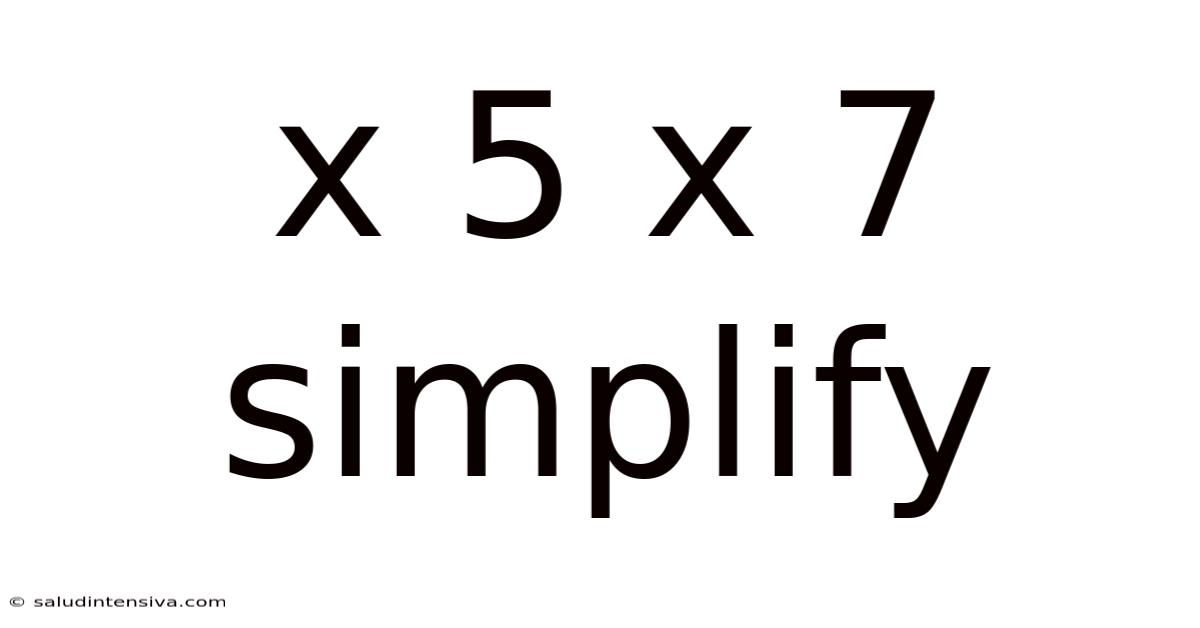
Table of Contents
Simplifying Fractions: A Deep Dive into x/5 x 7
Understanding how to simplify fractions is a fundamental skill in mathematics, crucial for everything from basic arithmetic to advanced calculus. This article will provide a comprehensive guide to simplifying fractions, specifically focusing on expressions like "x/5 x 7," exploring the underlying principles, offering step-by-step examples, and addressing common misconceptions. We'll delve into the concepts of prime factorization, greatest common divisors, and how these tools are instrumental in reducing fractions to their simplest form. This guide is designed for learners of all levels, from those just beginning to grasp fractions to those looking to solidify their understanding.
Understanding Fractions and Simplification
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (the top number) and the denominator (the bottom number). For example, in the fraction 3/4, 3 is the numerator and 4 is the denominator. Simplifying a fraction means reducing it to its lowest terms, where the numerator and denominator have no common factors other than 1. This makes the fraction easier to understand and work with.
The expression "x/5 x 7" is slightly ambiguous. It could be interpreted in two ways:
- (x/5) x 7: This implies multiplying the fraction x/5 by 7.
- x/(5 x 7): This means x is divided by the product of 5 and 7.
We'll address both interpretations separately.
Interpretation 1: (x/5) x 7
This expression involves multiplying a fraction by a whole number. The process is straightforward:
Step 1: Rewrite the whole number as a fraction. We can express 7 as the fraction 7/1.
Step 2: Multiply the numerators and denominators. This gives us:
(x/5) x (7/1) = (x * 7) / (5 * 1) = 7x/5
Step 3: Check for simplification. In this case, unless 'x' itself contains a factor of 5, the fraction 7x/5 is already in its simplest form. If, for example, x = 5, then the fraction becomes (75)/5 = 7. If x = 10, then the fraction becomes (710)/5 = 14. The simplification depends entirely on the value of x.
Example: If x = 10, then (x/5) x 7 = (10/5) x 7 = 2 x 7 = 14. If x = 15, then (x/5) x 7 = (15/5) x 7 = 3 x 7 = 21.
Interpretation 2: x/(5 x 7)
This interpretation involves dividing x by the product of 5 and 7.
Step 1: Calculate the denominator. 5 x 7 = 35. The expression becomes x/35.
Step 2: Check for simplification. This fraction is simplified unless x has a common factor with 35. The prime factorization of 35 is 5 x 7. Therefore, x can only be simplified if it is a multiple of 5 or 7.
Example:
- If x = 35, then x/35 = 35/35 = 1.
- If x = 70, then x/35 = 70/35 = 2.
- If x = 10, then x/35 = 10/35. This can be simplified by dividing both the numerator and denominator by their greatest common divisor (GCD), which is 5. 10/5 = 2 and 35/5 = 7. Therefore, 10/35 simplifies to 2/7.
- If x is a prime number that is not 5 or 7 (e.g., x = 2, 3, 11, etc.), the fraction x/35 will remain in its simplest form.
The Role of Prime Factorization and Greatest Common Divisor (GCD)
To effectively simplify fractions, understanding prime factorization and the GCD is essential.
-
Prime Factorization: This is the process of expressing a number as a product of its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11, etc.). For example, the prime factorization of 12 is 2 x 2 x 3 (or 2² x 3).
-
Greatest Common Divisor (GCD): This is the largest number that divides both the numerator and denominator without leaving a remainder. Finding the GCD allows us to simplify a fraction to its lowest terms. One method to find the GCD is to list all the factors of both the numerator and denominator and identify the largest common factor. Another efficient method is the Euclidean algorithm, especially useful for larger numbers.
Example using GCD: Let's simplify 18/24.
- Prime Factorization: 18 = 2 x 3 x 3 and 24 = 2 x 2 x 2 x 3.
- Identify Common Factors: Both 18 and 24 share two factors of 2 and one factor of 3.
- Calculate GCD: The GCD is 2 x 3 = 6.
- Simplify the Fraction: Divide both the numerator and denominator by the GCD: 18/6 = 3 and 24/6 = 4. Therefore, 18/24 simplifies to 3/4.
Step-by-Step Guide to Simplifying Fractions
- Find the Prime Factorization of the Numerator and Denominator: Break down both numbers into their prime factors.
- Identify Common Factors: Look for prime factors that appear in both the numerator and denominator.
- Cancel Out Common Factors: Divide both the numerator and denominator by each common factor.
- Multiply the Remaining Factors: Multiply the remaining prime factors in the numerator and denominator to obtain the simplified fraction.
Common Mistakes to Avoid
- Incorrect Cancellation: Students sometimes incorrectly cancel numbers that are not common factors. Remember, you can only cancel out common factors that are multiplied, not added or subtracted. For example, (2 + 3)/6 cannot be simplified to 2/6 + 3/6 (though that is mathematically correct), and neither can it be simplified to 5/6.
- Forgetting to Check for Further Simplification: Always ensure that the simplified fraction cannot be reduced further.
- Not Understanding Prime Factorization: A firm grasp of prime factorization is crucial for simplifying complex fractions efficiently.
Frequently Asked Questions (FAQ)
-
Q: What if the numerator is larger than the denominator?
- A: This is called an improper fraction. It can be simplified in the same way as a proper fraction (numerator smaller than denominator). It can also be converted into a mixed number (a whole number and a fraction).
-
Q: What if the numerator and denominator have no common factors other than 1?
- A: The fraction is already in its simplest form.
-
Q: Can I simplify fractions with variables?
- A: Yes, the same principles apply. You can simplify by canceling common factors, including variables, but you must ensure that the variables are present in both the numerator and denominator as multiplied factors.
Conclusion
Simplifying fractions is a fundamental skill in mathematics. By mastering prime factorization, understanding the greatest common divisor, and following the steps outlined in this guide, you can confidently simplify any fraction, including expressions like "x/5 x 7," regardless of the interpretation. Remember to always check for further simplification after each step and avoid common mistakes to ensure accuracy. Practice is key to developing fluency and confidence in simplifying fractions. With consistent effort, this seemingly simple task will become second nature, paving the way for success in more advanced mathematical concepts.
Latest Posts
Latest Posts
-
Graph Of X 2 9
Sep 21, 2025
-
90 Days From September 6
Sep 21, 2025
-
55 Degrees Fahrenheit In Celsius
Sep 21, 2025
-
3 10 As A Number
Sep 21, 2025
-
Hp To Kw Conversion Formula
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about X 5 X 7 Simplify . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.