Graph Of X 2 9
saludintensiva
Sep 21, 2025 · 6 min read
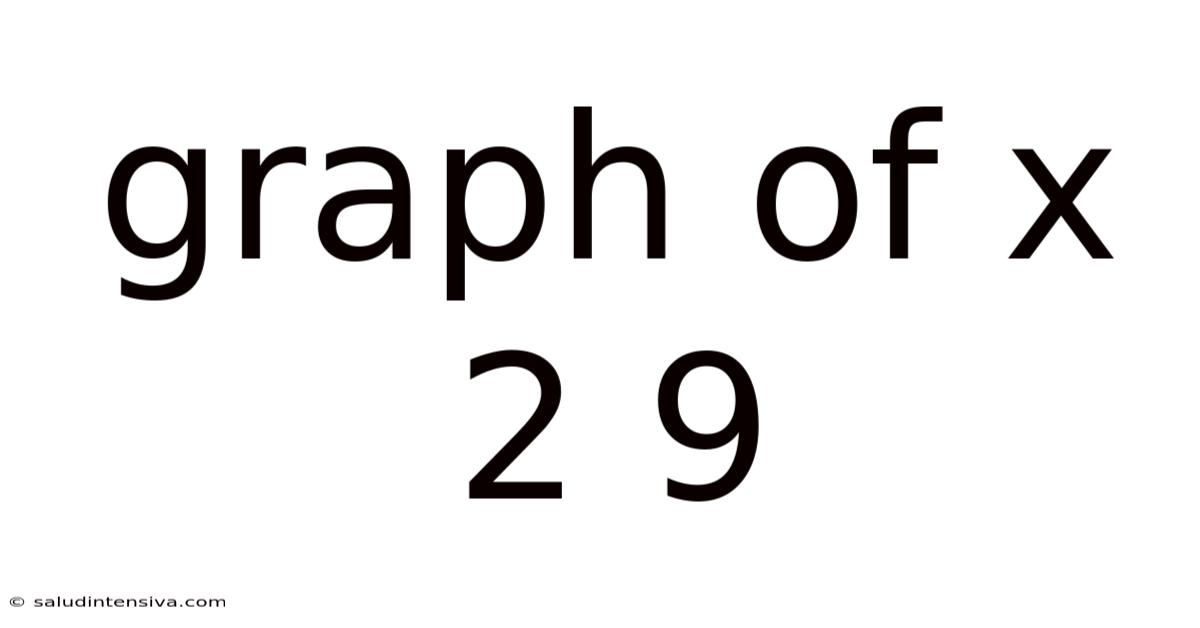
Table of Contents
Exploring the Graph of x² + 9: A Comprehensive Guide
The equation x² + 9 might seem deceptively simple at first glance. However, understanding its graphical representation unlocks a deeper understanding of fundamental concepts in algebra and coordinate geometry. This article will explore the graph of x² + 9 in detail, covering its properties, how to sketch it, and its implications within broader mathematical contexts. We'll delve into its characteristics, comparing it to the parent function y = x², and examining its transformations. This comprehensive guide is designed for students and anyone wanting to strengthen their understanding of quadratic functions and their graphical representations.
Introduction: Understanding Quadratic Functions
Before diving into the specifics of x² + 9, let's establish a foundation in quadratic functions. A quadratic function is a polynomial function of degree two, meaning the highest power of the variable (in this case, x) is 2. The general form of a quadratic function is written as:
y = ax² + bx + c
where a, b, and c are constants, and a ≠ 0. The graph of a quadratic function is always a parabola, a U-shaped curve. The parabola opens upwards (concave up) if a > 0 and opens downwards (concave down) if a < 0. The vertex of the parabola represents either the minimum (if a > 0) or maximum (if a < 0) point of the function.
The Specific Case of x² + 9
Our focus is on the function y = x² + 9. Notice that in this case, a = 1, b = 0, and c = 9. This means:
- a > 0: The parabola opens upwards.
- b = 0: The parabola is symmetric about the y-axis. This means the vertex lies directly on the y-axis.
- c = 9: The y-intercept is 9. This is the point where the parabola intersects the y-axis (where x = 0).
Steps to Sketch the Graph
Sketching the graph of y = x² + 9 is straightforward. We can use the properties we've identified to guide our drawing:
-
Plot the y-intercept: Since c = 9, the graph passes through the point (0, 9). This is the vertex of the parabola because the parabola is symmetric around the y-axis and opens upwards.
-
Determine the vertex: The vertex is located at (0, 9). Because b = 0, there's no horizontal shift from the parent function.
-
Plot additional points: Choose a few x-values (positive and negative) to find corresponding y-values. For example:
- If x = 1, y = 1² + 9 = 10. Point: (1, 10)
- If x = -1, y = (-1)² + 9 = 10. Point: (-1, 10)
- If x = 2, y = 2² + 9 = 13. Point: (2, 13)
- If x = -2, y = (-2)² + 9 = 13. Point: (-2, 13)
-
Sketch the parabola: Connect the points you've plotted with a smooth, U-shaped curve. Remember that the parabola is symmetric around the y-axis, so the points on the left side of the y-axis mirror those on the right side.
Comparing to the Parent Function y = x²
The graph of y = x² + 9 is a vertical translation of the parent function y = x². This means it's essentially the same parabola, but shifted upwards by 9 units. The parent function y = x² has its vertex at (0, 0), while y = x² + 9 has its vertex at (0, 9). All other characteristics, such as the upward opening and symmetry around the y-axis, remain unchanged.
Analyzing Key Features of the Graph
Let's summarize the key features of the graph of y = x² + 9:
- Vertex: (0, 9) – This is the minimum point of the parabola.
- Axis of Symmetry: x = 0 (the y-axis) – The parabola is symmetric about this vertical line.
- Y-intercept: (0, 9) – The point where the parabola intersects the y-axis.
- X-intercepts (roots): None. The parabola does not intersect the x-axis because x² is always non-negative, and adding 9 to it always results in a positive y-value.
- Range: [9, ∞) – The y-values of the graph range from 9 (inclusive) to infinity.
- Domain: (-∞, ∞) – The x-values of the graph span all real numbers.
The Absence of x-intercepts: Implications and Interpretation
The fact that the graph of y = x² + 9 has no x-intercepts is significant. X-intercepts represent the roots or solutions of the quadratic equation when y = 0. In this case, the equation x² + 9 = 0 has no real solutions. To find the solutions, we would have x² = -9, which means x = ±√(-9). This results in imaginary solutions (x = ±3i), indicating that the parabola never crosses the x-axis.
Mathematical Applications and Extensions
Understanding the graph of x² + 9 extends beyond simple graphing. It plays a role in various mathematical contexts, including:
-
Solving Quadratic Inequalities: The graph can be used to visualize the solution set for inequalities involving x² + 9. For example, solving x² + 9 > 0 would show that the inequality is true for all real numbers x.
-
Calculus: The concept of derivatives and integrals applies to this function as well. The derivative represents the slope of the tangent line at any point on the parabola, while the integral represents the area under the curve.
-
Transformations of Functions: Understanding the vertical shift in this function provides a basis for grasping other transformations of functions, such as horizontal shifts, reflections, and stretches/compressions.
Frequently Asked Questions (FAQ)
Q1: What is the significance of the "9" in the equation y = x² + 9?
A1: The "9" represents the vertical shift of the parent function y = x². It shifts the entire parabola upwards by 9 units.
Q2: Why doesn't the graph of y = x² + 9 have any x-intercepts?
A2: Because x² is always non-negative, adding 9 to it always results in a positive value. Therefore, the function y = x² + 9 is always positive, and its graph never intersects the x-axis.
Q3: How does the graph of y = x² + 9 differ from the graph of y = x² - 9?
A3: The graph of y = x² - 9 is a downward shift of the parent function y = x² by 9 units. It will intersect the x-axis at x = ±3. The graph of y = x² + 9, as discussed, is shifted upwards and does not intersect the x-axis.
Q4: Can this graph be used to model real-world scenarios?
A4: While not as common as parabolas that intersect the x-axis, this type of graph could potentially represent scenarios where a minimum value exists but there's no point where the dependent variable reaches zero. Think of a scenario where a cost function has a minimum value but never actually reaches zero cost.
Conclusion: A Deeper Understanding
The seemingly simple equation y = x² + 9 reveals a wealth of information about quadratic functions and their graphical representations. By understanding its properties, such as its vertex, axis of symmetry, and the absence of x-intercepts, we can gain a more profound understanding of the behavior of quadratic functions and their applications in various mathematical fields. This exploration underscores the importance of analyzing even seemingly straightforward equations to unlock deeper mathematical insights. The ability to visualize and interpret this type of graph is a crucial skill for students progressing in their mathematical studies. Remember, the key lies in connecting the algebraic representation with its geometric counterpart for a comprehensive understanding.
Latest Posts
Latest Posts
-
Area Of L Shape Formula
Sep 21, 2025
-
X 2 5x 4 Factored
Sep 21, 2025
-
400 Square Feet To Meters
Sep 21, 2025
-
How Much Time Until 12 30
Sep 21, 2025
-
X 2 10x 25 Factor
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about Graph Of X 2 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.