X 2 5x 4 Factored
saludintensiva
Sep 21, 2025 · 6 min read
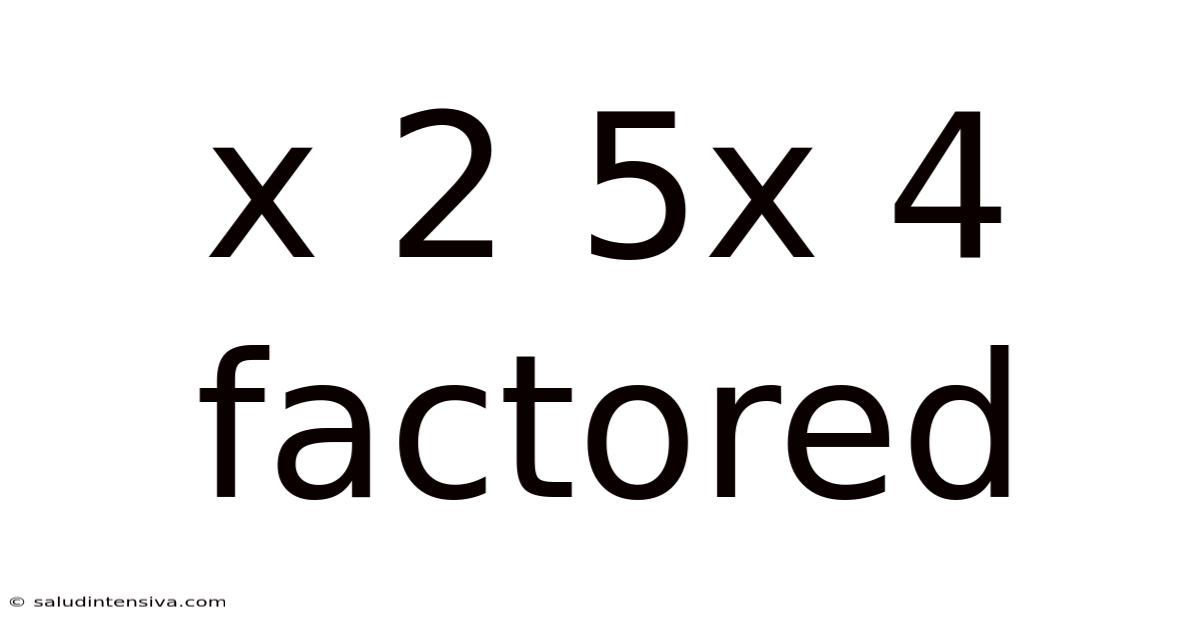
Table of Contents
Factoring Quadratic Expressions: A Deep Dive into x² + 5x + 4
Understanding how to factor quadratic expressions is a fundamental skill in algebra. It's a stepping stone to more advanced concepts, and mastering it unlocks the ability to solve a wide range of mathematical problems. This article will provide a comprehensive guide to factoring, specifically focusing on the expression x² + 5x + 4, but also offering broader techniques applicable to other quadratic expressions. We'll explore the process step-by-step, delve into the underlying mathematical principles, and answer frequently asked questions.
Understanding Quadratic Expressions
Before we dive into factoring x² + 5x + 4, let's define what a quadratic expression is. A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (usually x) is 2. It generally takes the form ax² + bx + c, where a, b, and c are constants, and a ≠ 0. Our example, x² + 5x + 4, fits this form perfectly, with a = 1, b = 5, and c = 4.
Factoring: The Reverse of Expanding
Factoring is essentially the reverse process of expanding (or multiplying) algebraic expressions. When we expand (x + p)(x + q), we use the distributive property (often remembered using the FOIL method: First, Outer, Inner, Last) to get x² + (p + q)x + pq. Factoring involves finding the values of p and q that, when added, give b and when multiplied, give c in the general quadratic expression ax² + bx + c.
Step-by-Step Factoring of x² + 5x + 4
Let's break down the factoring of x² + 5x + 4 step-by-step:
-
Identify a, b, and c: In our expression, a = 1, b = 5, and c = 4.
-
Find two numbers that add up to b and multiply to c: We need to find two numbers that add up to 5 (our b value) and multiply to 4 (our c value). Let's list the factor pairs of 4:
- 1 and 4
- -1 and -4
- 2 and 2
- -2 and -2
-
Determine the correct pair: Out of these pairs, only 1 and 4 satisfy both conditions: 1 + 4 = 5 (our b value) and 1 * 4 = 4 (our c value).
-
Write the factored form: Now that we've found our numbers (1 and 4), we can write the factored form of the quadratic expression: (x + 1)(x + 4).
Therefore, the factored form of x² + 5x + 4 is (x + 1)(x + 4). We can verify this by expanding (x + 1)(x + 4) using the FOIL method:
- First: x * x = x²
- Outer: x * 4 = 4x
- Inner: 1 * x = x
- Last: 1 * 4 = 4
Combining these terms gives us x² + 4x + x + 4 = x² + 5x + 4, confirming our factorization is correct.
Factoring More Complex Quadratic Expressions
While the example above involved a relatively simple quadratic expression where a = 1, the process is similar even when 'a' is not 1 or when dealing with negative numbers. Let's consider a more complex example: 2x² + 7x + 3.
-
Identify a, b, and c: Here, a = 2, b = 7, and c = 3.
-
Find two numbers that multiply to ac and add to b: We need two numbers that multiply to (a * c) = (2 * 3) = 6 and add up to 7 (our b value). These numbers are 1 and 6.
-
Rewrite the expression: Rewrite the middle term (7x) using these two numbers: 2x² + 1x + 6x + 3.
-
Factor by grouping: Group the terms in pairs and factor out the greatest common factor (GCF) from each pair:
x(2x + 1) + 3(2x + 1)
-
Factor out the common binomial: Notice that (2x + 1) is a common factor in both terms. Factor it out: (2x + 1)(x + 3).
Therefore, the factored form of 2x² + 7x + 3 is (2x + 1)(x + 3). Again, you can verify this by expanding.
The Significance of Factoring
The ability to factor quadratic expressions is crucial for several reasons:
-
Solving Quadratic Equations: Factoring is a primary method for solving quadratic equations (equations of the form ax² + bx + c = 0). Once factored, the solutions (roots) can be easily found by setting each factor equal to zero. For example, if (x + 1)(x + 4) = 0, then either x + 1 = 0 or x + 4 = 0, giving solutions x = -1 and x = -4.
-
Simplifying Expressions: Factoring simplifies complex algebraic expressions, making them easier to manipulate and understand. This is essential in various mathematical applications.
-
Graphing Quadratic Functions: The factored form of a quadratic expression reveals the x-intercepts (where the graph crosses the x-axis) of the corresponding quadratic function. These intercepts are crucial for sketching the graph accurately.
-
Foundation for Advanced Algebra: Factoring is a fundamental skill that builds a strong base for more advanced algebraic concepts, such as working with rational expressions, solving systems of equations, and calculus.
Dealing with Negative Coefficients
When dealing with negative coefficients in the quadratic expression, the process remains the same, but extra care must be taken with signs. Consider the expression x² - 5x + 6.
-
Identify a, b, and c: a = 1, b = -5, and c = 6.
-
Find two numbers that add to b and multiply to c: We need two numbers that add up to -5 and multiply to 6. These numbers are -2 and -3.
-
Write the factored form: (x - 2)(x - 3)
Therefore, x² - 5x + 6 factors to (x - 2)(x - 3).
The Case of Prime Polynomials
Not all quadratic expressions can be factored using integers. Some are prime polynomials, meaning they cannot be factored into simpler expressions using integer coefficients. For example, x² + x + 1 is a prime polynomial. In such cases, other methods like the quadratic formula might be necessary to find the roots.
Frequently Asked Questions (FAQ)
-
What if 'a' is not 1? As shown in the example 2x² + 7x + 3, you can use the method of factoring by grouping or other techniques like the AC method to factor quadratic expressions where 'a' is not equal to 1.
-
What is the quadratic formula? The quadratic formula is an alternative method for solving quadratic equations, especially useful when factoring is difficult or impossible. The formula is: x = [-b ± √(b² - 4ac)] / 2a.
-
How can I check my factoring? Always expand your factored expression to verify it returns the original quadratic expression.
Conclusion
Factoring quadratic expressions is a crucial skill in algebra, providing a pathway to solving equations, simplifying expressions, and understanding graphical representations of quadratic functions. While the process might seem challenging at first, with consistent practice and a clear understanding of the underlying principles, mastering this skill becomes significantly easier. Remember to carefully consider the signs of the coefficients and to always check your work by expanding the factored expression. Understanding the different approaches and recognizing when a polynomial is prime are equally important aspects of developing proficiency in this area of algebra. By applying the techniques explained in this article, you'll develop confidence and a solid foundation for tackling more complex mathematical problems in the future.
Latest Posts
Latest Posts
-
X 2 8x 12 Factor
Sep 21, 2025
-
Random Phone Numbers In Canada
Sep 21, 2025
-
Two Step Equations With Decimals
Sep 21, 2025
-
Convert 36 C To Fahrenheit
Sep 21, 2025
-
Cm Squared To In Squared
Sep 21, 2025
Related Post
Thank you for visiting our website which covers about X 2 5x 4 Factored . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.