1 7 As A Percent
saludintensiva
Sep 17, 2025 · 5 min read
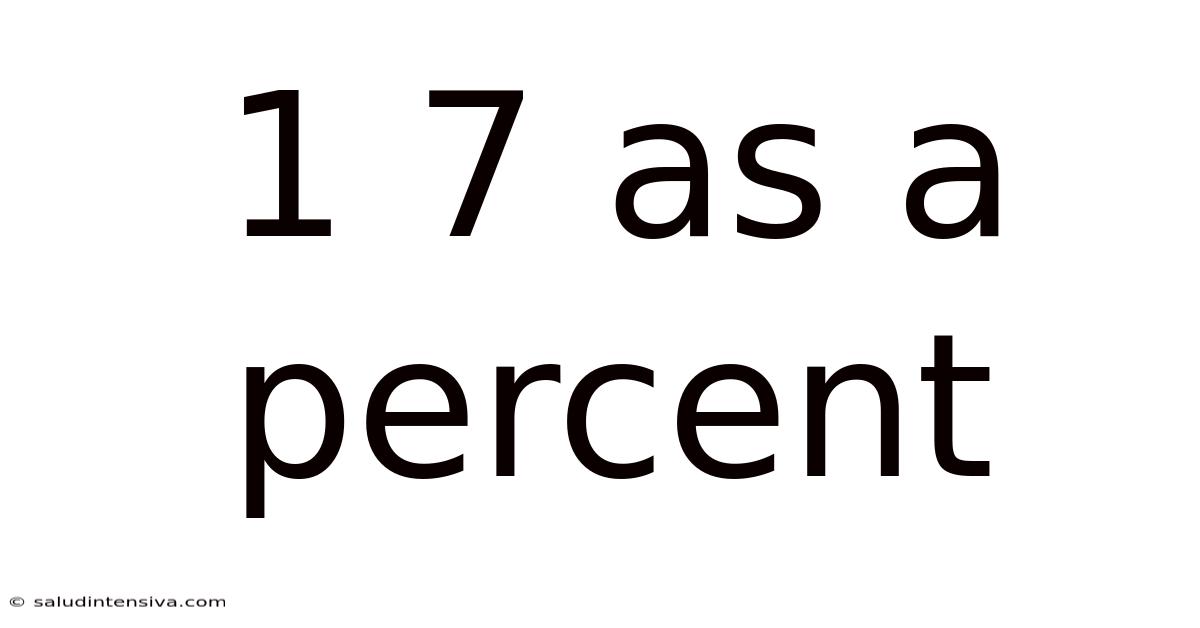
Table of Contents
Understanding 1/7 as a Percentage: A Comprehensive Guide
Understanding fractions and their percentage equivalents is a fundamental skill in mathematics with applications across numerous fields, from finance and statistics to everyday life. This article delves into the specifics of converting the fraction 1/7 into a percentage, exploring various methods, providing a detailed explanation, and addressing common misconceptions. We'll explore the practical implications and offer some advanced insights for those seeking a deeper understanding.
Introduction: The Significance of Percentage Conversions
The ability to convert fractions to percentages is crucial for several reasons. Percentages provide a standardized way to compare different proportions and represent parts of a whole. Whether you're calculating discounts, interest rates, or analyzing statistical data, understanding how to express fractions as percentages is essential. This article focuses specifically on the fraction 1/7, a recurring decimal that presents a unique challenge in the conversion process.
Method 1: Direct Conversion using Division
The most straightforward method to convert a fraction to a percentage involves dividing the numerator by the denominator and then multiplying the result by 100. In the case of 1/7:
- Divide: 1 ÷ 7 ≈ 0.142857142857...
- Multiply by 100: 0.142857142857... × 100 ≈ 14.2857%
Notice the repeating decimal. This is characteristic of converting fractions with denominators that are not factors of 10 (or powers of 10). We often round this result to a reasonable number of decimal places, commonly two (14.29%) or three (14.286%). The choice depends on the level of precision required for the particular application.
Method 2: Using Long Division for Precision
For those needing a more precise understanding of the decimal representation of 1/7, long division provides a detailed approach. Let's walk through the process:
- Setup: Set up the long division problem with 1 as the dividend and 7 as the divisor.
- Division: Perform the long division. You'll quickly notice a repeating pattern in the quotient: 0.142857142857... The digits 142857 repeat infinitely.
- Conversion to Percentage: Multiply the resulting decimal by 100 to obtain the percentage.
This method emphasizes the nature of the repeating decimal, highlighting why a precise representation of 1/7 as a percentage requires either rounding or using the repeating decimal notation (14.2857...).
Understanding the Repeating Decimal: A Deeper Dive
The repeating decimal 0.142857... is a fascinating mathematical concept. The sequence of digits (142857) repeats infinitely. This is a consequence of the fact that 7 is a prime number and not a factor of any power of 10. Numbers with denominators that are multiples of 2 and/or 5 will always result in terminating decimals, while numbers with prime factors other than 2 and 5 will result in repeating decimals.
Practical Applications of 1/7 as a Percentage
While 1/7 might not appear as frequently in everyday calculations as other fractions, understanding its percentage equivalent is valuable in various contexts:
- Statistics: In statistical analysis, you might encounter situations where you need to represent a proportion as a percentage, and 1/7 could be relevant.
- Finance: Certain financial calculations, especially those involving complex interest rates or proportions of investments, might require the conversion of fractions like 1/7 to percentages.
- Science: In scientific experiments involving proportions or ratios, understanding the percentage equivalent of 1/7 can be crucial for interpreting results.
- Everyday Life: Imagine dividing a pizza into seven slices; one slice represents approximately 14.29% of the whole pizza.
Common Misconceptions about Percentage Conversions
A common mistake is to simply multiply the numerator by 100 and then divide by the denominator. This incorrect approach would yield 1400%, which is clearly wrong. Remember the correct process is to divide the numerator by the denominator before multiplying by 100.
Another misconception is believing that a repeating decimal represents an imprecise value. While it's true that we often round repeating decimals for practical use, the repeating decimal itself is a perfectly precise mathematical representation of the fraction. It simply requires a different notation to capture its infinite nature.
Frequently Asked Questions (FAQ)
-
Q: Why does 1/7 produce a repeating decimal?
- A: Because 7 is a prime number that doesn't divide evenly into any power of 10.
-
Q: How many decimal places should I round 1/7 to?
- A: The appropriate number of decimal places depends on the context. Two or three decimal places (14.29% or 14.286%) are usually sufficient for most applications. For scientific or engineering applications, more precision might be necessary.
-
Q: Can 1/7 be expressed as an exact percentage?
- A: No, not as a terminating decimal. Its precise representation includes the repeating decimal 0.142857...
-
Q: What are some other fractions that produce repeating decimals when converted to percentages?
- A: Fractions with denominators that contain prime factors other than 2 and 5 will produce repeating decimals. Examples include 1/3 (33.33...), 1/6 (16.66...), and 1/9 (11.11...).
Advanced Concepts: Continued Fractions
For those interested in exploring more advanced mathematical concepts, the fraction 1/7 can be represented as a continued fraction:
[0; 7]
This representation provides another way to understand the nature of the fraction and its decimal expansion. Continued fractions offer a unique approach to representing rational and irrational numbers.
Conclusion: Mastering Fraction-to-Percentage Conversions
Converting fractions to percentages is a critical skill with widespread applications. This detailed exploration of converting 1/7 to a percentage, along with explanations of repeating decimals and various conversion methods, equips you with a robust understanding of this fundamental mathematical concept. Remember to choose the appropriate level of precision for your specific needs and always prioritize accuracy in your calculations. By understanding the underlying principles, you can confidently tackle similar fraction-to-percentage conversions and apply this knowledge in various real-world situations. This foundational skill will benefit you across various academic and professional settings, solidifying your grasp of mathematical principles and their practical applications.
Latest Posts
Latest Posts
-
3 2 5 As A Decimal
Sep 17, 2025
-
1 9 16 To Decimal
Sep 17, 2025
-
27 To The Power Of
Sep 17, 2025
-
Whats Equivalent To 1 4
Sep 17, 2025
-
23 6 As A Mixed Number
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 1 7 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.