23/6 As A Mixed Number
saludintensiva
Sep 17, 2025 · 6 min read
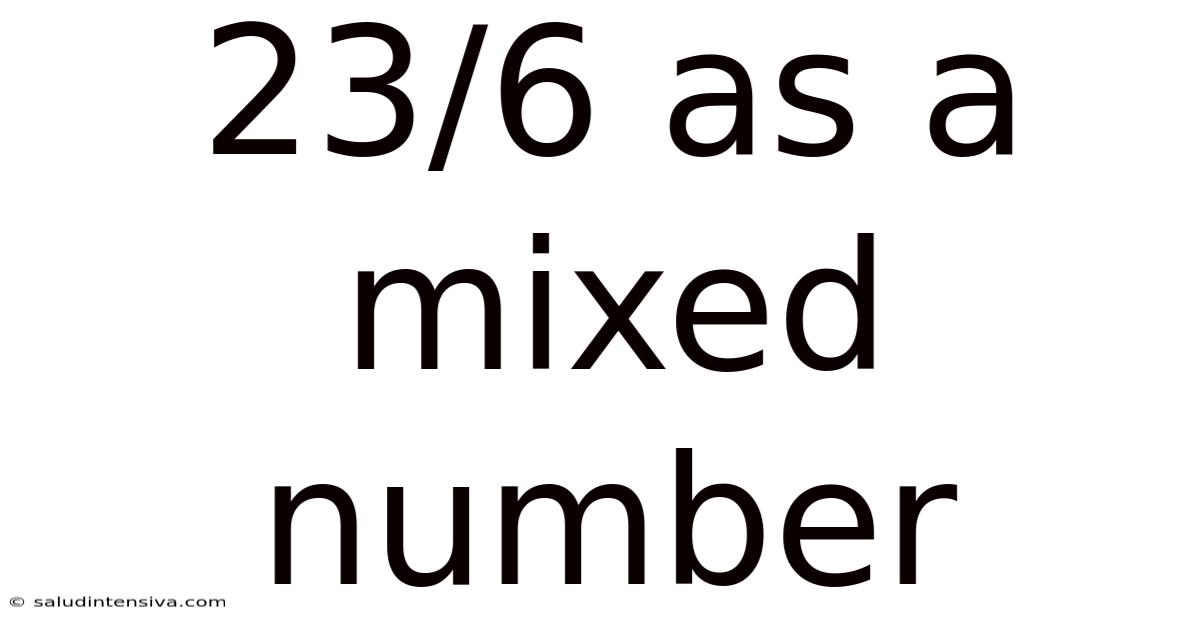
Table of Contents
Understanding 23/6 as a Mixed Number: A Comprehensive Guide
The fraction 23/6 represents a value greater than one. Understanding how to convert improper fractions like 23/6 into mixed numbers is a fundamental skill in arithmetic. This comprehensive guide will not only show you how to convert 23/6 into a mixed number but also why the process works, exploring the underlying mathematical concepts and providing plenty of practice examples. We’ll also address frequently asked questions and delve into the practical applications of mixed numbers.
Introduction to Fractions and Mixed Numbers
Before we dive into converting 23/6, let's review the basics. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator shows how many of those parts are being considered.
An improper fraction is a fraction where the numerator is greater than or equal to the denominator (e.g., 23/6, 7/4, 9/9). This indicates a value greater than or equal to one.
A mixed number combines a whole number and a proper fraction (a fraction where the numerator is less than the denominator, e.g., 1/2, 3/4). It represents the same value as an improper fraction but in a more easily understandable format. For example, 1 1/2 is a mixed number that represents the same value as the improper fraction 3/2.
Converting 23/6 to a Mixed Number: Step-by-Step
The conversion process involves dividing the numerator by the denominator. Here’s how to convert 23/6:
-
Divide the numerator by the denominator: 23 ÷ 6 = 3 with a remainder of 5.
-
The quotient becomes the whole number part of the mixed number: The quotient (3) is the whole number part of our mixed number.
-
The remainder becomes the numerator of the fractional part: The remainder (5) becomes the numerator of the fraction in our mixed number.
-
The denominator remains the same: The denominator (6) stays the same.
Therefore, 23/6 as a mixed number is 3 5/6.
This means that 23/6 represents three whole units and five-sixths of another unit.
Visualizing the Conversion
Imagine you have 23 identical objects. You want to group them into sets of 6. You can create three complete sets of 6, leaving you with 5 objects remaining. This visually represents the mixed number 3 5/6. Each complete set of 6 represents a whole number (1), and the remaining 5 objects represent the fractional part (5/6).
Why This Method Works: A Deeper Dive
The conversion from an improper fraction to a mixed number is essentially a representation of the division algorithm. When we divide 23 by 6, we're finding out how many times 6 goes into 23 completely. The quotient represents the number of times 6 fits entirely into 23, which gives us the whole number part of the mixed number. The remainder represents the portion of 6 that's left over, which becomes the numerator of the fractional part. The denominator remains unchanged because we're still dealing with parts of the original unit (which was divided into six equal parts).
Mathematically, we can express this as:
23/6 = (6 * 3 + 5) / 6 = (6 * 3) / 6 + 5/6 = 3 + 5/6 = 3 5/6
Converting Mixed Numbers Back to Improper Fractions
It's equally important to understand how to reverse the process. To convert a mixed number back into an improper fraction:
-
Multiply the whole number by the denominator: 3 x 6 = 18
-
Add the numerator: 18 + 5 = 23
-
The result becomes the new numerator: 23
-
The denominator remains the same: 6
Therefore, 3 5/6 converts back to the improper fraction 23/6.
Practical Applications of Mixed Numbers
Mixed numbers are frequently used in everyday life and across various fields:
-
Measurement: Imagine you're measuring ingredients for a recipe. You might need 2 1/2 cups of flour or 1 3/4 teaspoons of baking powder. Mixed numbers provide a convenient way to express these measurements.
-
Time: We commonly use mixed numbers to represent time. For example, 1 hour and 30 minutes is expressed as 1 1/2 hours.
-
Construction: Carpenters, builders, and other tradespeople frequently use mixed numbers when dealing with measurements and materials.
-
Data Analysis: In statistics and data analysis, mixed numbers can appear in representing averages or proportions.
-
Everyday Fractions: Many everyday situations involve parts of wholes, making mixed numbers a practical way to represent these quantities accurately.
More Examples of Improper Fraction to Mixed Number Conversions
Let's practice with a few more examples:
-
17/5: 17 ÷ 5 = 3 with a remainder of 2. Therefore, 17/5 = 3 2/5.
-
29/8: 29 ÷ 8 = 3 with a remainder of 5. Therefore, 29/8 = 3 5/8.
-
41/12: 41 ÷ 12 = 3 with a remainder of 5. Therefore, 41/12 = 3 5/12.
-
100/7: 100 ÷ 7 = 14 with a remainder of 2. Therefore, 100/7 = 14 2/7
Simplifying Fractions
Sometimes, the fractional part of a mixed number can be simplified. For example, if we had obtained 4 6/12, we could simplify the fraction 6/12 by dividing both the numerator and denominator by their greatest common divisor (GCD), which is 6. This would simplify the mixed number to 4 1/2. Always check if the fractional part can be simplified to its lowest terms.
Frequently Asked Questions (FAQ)
Q: What if the remainder is zero?
A: If the remainder is zero, it means the improper fraction is a whole number. For instance, 18/6 = 3 (because 18 ÷ 6 = 3 with a remainder of 0). There's no fractional part.
Q: Can I use a calculator to convert improper fractions to mixed numbers?
A: Yes, many calculators have the capability to perform this conversion. However, understanding the underlying process is crucial for problem-solving and building a strong foundation in mathematics.
Q: Why is it important to learn about mixed numbers?
A: Mixed numbers provide a more intuitive and practical way to represent quantities greater than one. They're essential for various applications in everyday life and different academic disciplines.
Q: Are there different ways to convert improper fractions to mixed numbers?
A: While the method described above is the most common and straightforward, there might be slightly different approaches depending on the teaching method or individual preference. However, the core principle of division remains the same.
Conclusion
Converting improper fractions like 23/6 into mixed numbers (3 5/6) is a fundamental mathematical skill with wide-ranging applications. Understanding the process involves division, recognizing the significance of the quotient and remainder, and applying this knowledge to various contexts. By mastering this skill, you’ll not only improve your arithmetic abilities but also gain a deeper understanding of fractions and their importance in practical problem-solving. Remember to practice regularly and always check for simplification opportunities within the resulting fractional part. The more you practice, the more confident and proficient you will become in working with fractions and mixed numbers.
Latest Posts
Latest Posts
-
15 Miles How Many Minutes
Sep 17, 2025
-
Is 6 8 Greater Than 3 4
Sep 17, 2025
-
1 3 2 2 3
Sep 17, 2025
-
16 3 As A Decimal
Sep 17, 2025
-
What Is Equal To 8 10
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 23/6 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.