10 1/2 As A Decimal
saludintensiva
Sep 11, 2025 · 4 min read
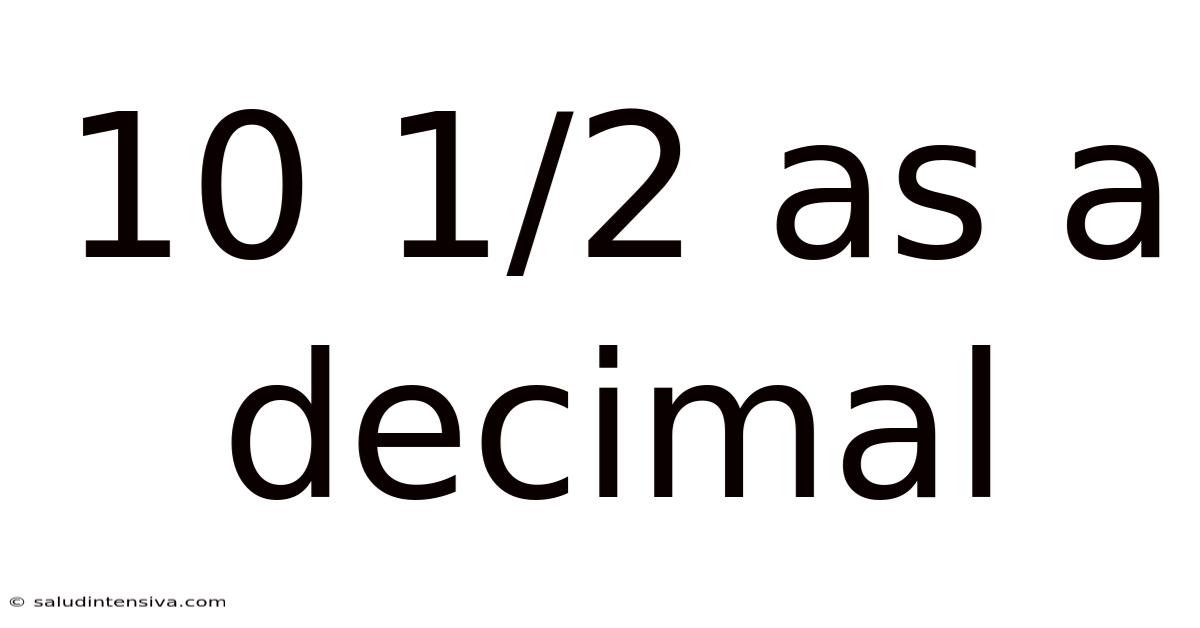
Table of Contents
10 1/2 as a Decimal: A Comprehensive Guide
Understanding how to convert fractions to decimals is a fundamental skill in mathematics. This comprehensive guide will delve into the conversion of the mixed number 10 1/2 into its decimal equivalent, exploring the underlying principles and providing various methods to achieve this. We'll also address common questions and misconceptions surrounding this type of conversion. By the end, you'll not only know the decimal value of 10 1/2 but also possess a solid understanding of fractional-to-decimal conversion techniques.
Understanding Mixed Numbers and Decimals
Before diving into the conversion, let's clarify some key terms. A mixed number combines a whole number and a fraction, like 10 1/2. A decimal is a number expressed in the base-10 system, using a decimal point to separate the whole number part from the fractional part (e.g., 10.5). Converting a mixed number to a decimal essentially means representing the same quantity using the decimal system.
Method 1: Converting the Fraction to a Decimal First
This method involves converting the fractional part of the mixed number into its decimal equivalent before adding the whole number.
-
Isolate the fraction: In 10 1/2, the fraction is 1/2.
-
Convert the fraction: To convert 1/2 to a decimal, we perform the division: 1 ÷ 2 = 0.5.
-
Combine with the whole number: Add the whole number part (10) to the decimal equivalent of the fraction (0.5): 10 + 0.5 = 10.5.
Therefore, 10 1/2 as a decimal is 10.5.
Method 2: Converting the Entire Mixed Number Directly
This method involves converting the entire mixed number into an improper fraction first and then converting that improper fraction to a decimal.
-
Convert to an improper fraction: To convert a mixed number to an improper fraction, we multiply the whole number by the denominator of the fraction, add the numerator, and keep the same denominator. For 10 1/2:
(10 x 2) + 1 = 21 The improper fraction is 21/2.
-
Convert the improper fraction to a decimal: Perform the division: 21 ÷ 2 = 10.5.
Again, we find that 10 1/2 as a decimal is 10.5.
Method 3: Understanding Place Value
This method leverages the understanding of place value in the decimal system.
The fraction 1/2 represents one-half, or 0.5. This means that the digit 5 represents five tenths. Therefore, 10 1/2 can be directly interpreted as 10 and 5 tenths, which is written as 10.5. This method highlights the direct relationship between the fractional part and its decimal representation.
Illustrative Examples: Extending the Concept
Let's extend this understanding by applying similar methods to other mixed numbers:
-
5 3/4:
- Method 1: 3/4 = 0.75; 5 + 0.75 = 5.75
- Method 2: (5 x 4) + 3 = 23; 23/4 = 5.75
- Therefore, 5 3/4 as a decimal is 5.75.
-
2 1/5:
- Method 1: 1/5 = 0.2; 2 + 0.2 = 2.2
- Method 2: (2 x 5) + 1 = 11; 11/5 = 2.2
- Therefore, 2 1/5 as a decimal is 2.2.
-
12 7/10:
- Method 1: 7/10 = 0.7; 12 + 0.7 = 12.7
- Method 2: (12 x 10) + 7 = 127; 127/10 = 12.7
- Therefore, 12 7/10 as a decimal is 12.7.
The Significance of Decimal Representation
Converting fractions to decimals is crucial for various reasons:
-
Ease of Calculation: Decimals are generally easier to add, subtract, multiply, and divide compared to fractions, especially when dealing with multiple fractions.
-
Real-world Applications: Decimals are commonly used in everyday life, such as measuring lengths, weights, monetary values, and representing percentages.
-
Scientific and Engineering Applications: Scientific and engineering calculations often rely heavily on decimal representations for precision and ease of computation.
Frequently Asked Questions (FAQ)
Q: Can all fractions be converted to terminating decimals?
A: No. Fractions with denominators that are not multiples of 2 or 5 (or combinations thereof) will result in repeating decimals. For example, 1/3 = 0.333... (a repeating decimal).
Q: What if the fraction is an improper fraction (numerator greater than the denominator)?
A: An improper fraction can be converted to a mixed number first, and then to a decimal using the methods described above, or you can directly divide the numerator by the denominator.
Q: Are there any shortcuts for converting common fractions to decimals?
A: Yes, memorizing the decimal equivalents of some common fractions (e.g., 1/2 = 0.5, 1/4 = 0.25, 1/5 = 0.2, 1/10 = 0.1) can significantly speed up the conversion process.
Conclusion
Converting 10 1/2 to a decimal is straightforward and can be achieved through several methods. This process underscores the fundamental relationship between fractions and decimals, which are simply different representations of the same numerical value. Mastering this conversion skill is essential for various mathematical applications and practical situations. By understanding the underlying principles and applying the methods explained in this guide, you can confidently tackle similar conversions with ease and accuracy. The ability to seamlessly move between fractions and decimals significantly enhances mathematical fluency and problem-solving capabilities. Remember, practice is key to mastering this valuable skill, so keep practicing and experimenting with different fractions!
Latest Posts
Latest Posts
-
What Is 6 16 Simplified
Sep 11, 2025
-
Lcm Of 10 And 11
Sep 11, 2025
-
Gcf Of 30 And 50
Sep 11, 2025
-
1 3rd As A Decimal
Sep 11, 2025
-
Scientific Notation Of Negative Numbers
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 10 1/2 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.