Lcm Of 10 And 11
saludintensiva
Sep 11, 2025 · 6 min read
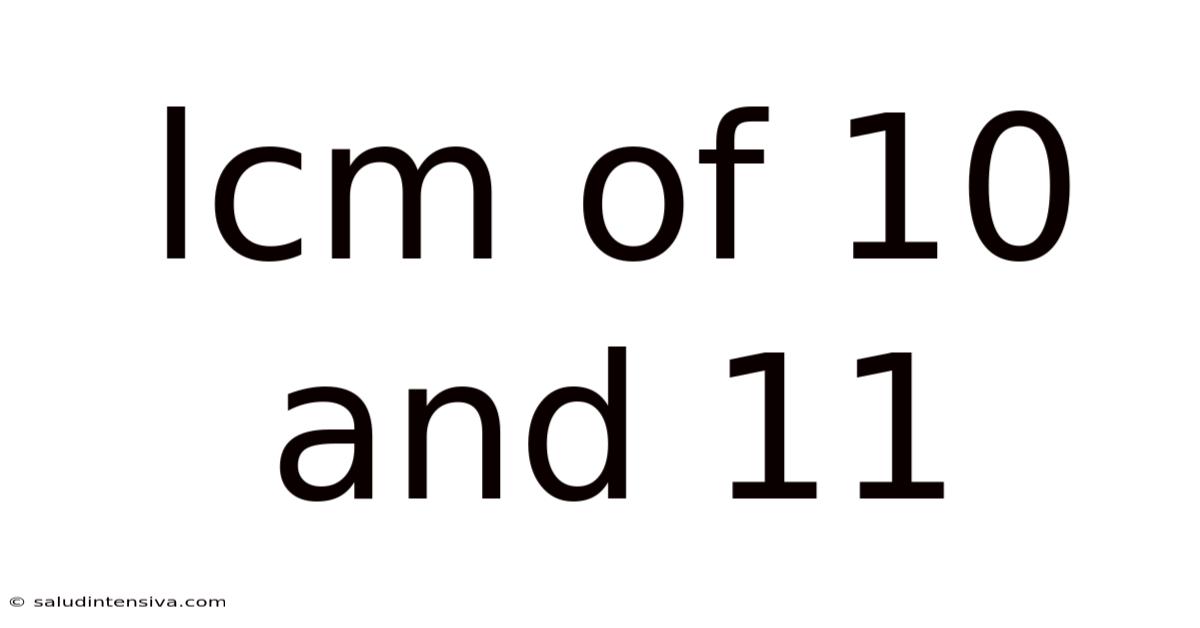
Table of Contents
Unveiling the Least Common Multiple (LCM) of 10 and 11: A Deep Dive into Number Theory
Finding the least common multiple (LCM) of two numbers might seem like a simple arithmetic task, especially for seemingly straightforward numbers like 10 and 11. However, understanding the underlying principles behind LCM calculations opens doors to a fascinating world of number theory and its practical applications. This article will not only reveal the LCM of 10 and 11 but also delve into the fundamental concepts, different methods of calculation, and the broader significance of LCMs in mathematics and beyond. We'll explore various approaches, from prime factorization to the use of the greatest common divisor (GCD), ensuring a comprehensive understanding for readers of all levels.
Understanding Least Common Multiples (LCMs)
Before we tackle the specific case of 10 and 11, let's establish a firm grasp of the concept of LCM. The least common multiple of two or more integers is the smallest positive integer that is divisible by all the given integers without leaving a remainder. Think of it as the smallest number that contains all the given numbers as its factors. For example, the LCM of 2 and 3 is 6 because 6 is the smallest positive integer divisible by both 2 and 3.
The concept of LCM is crucial in various mathematical contexts, including:
- Fraction addition and subtraction: Finding a common denominator when adding or subtracting fractions requires determining the LCM of the denominators.
- Scheduling and cyclical events: Determining when two cyclical events will coincide (e.g., two buses arriving at the same stop simultaneously) often involves calculating the LCM of their cycles.
- Modular arithmetic: LCM plays a vital role in solving problems related to congruences and modular arithmetic, which have widespread applications in cryptography and computer science.
- Abstract algebra: The concept of LCM extends to more advanced mathematical structures like rings and ideals.
Calculating the LCM of 10 and 11: Method 1 – Prime Factorization
The most fundamental method for finding the LCM involves prime factorization. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself (e.g., 2, 3, 5, 7, 11). Prime factorization breaks down a number into its prime factors.
Let's apply this method to find the LCM of 10 and 11:
- Prime factorization of 10: 10 = 2 × 5
- Prime factorization of 11: 11 is a prime number, so its prime factorization is simply 11.
Now, to find the LCM, we take the highest power of each prime factor present in the factorizations:
- The prime factors are 2, 5, and 11.
- The highest power of 2 is 2¹ = 2.
- The highest power of 5 is 5¹ = 5.
- The highest power of 11 is 11¹ = 11.
Multiply these highest powers together: 2 × 5 × 11 = 110
Therefore, the LCM of 10 and 11 is 110.
Calculating the LCM of 10 and 11: Method 2 – Using the Greatest Common Divisor (GCD)
Another efficient method utilizes the relationship between the LCM and the greatest common divisor (GCD). The GCD of two numbers is the largest positive integer that divides both numbers without leaving a remainder. There's a fundamental theorem linking LCM and GCD:
LCM(a, b) × GCD(a, b) = a × b
where 'a' and 'b' are the two numbers.
Let's apply this to find the LCM of 10 and 11:
-
Find the GCD of 10 and 11: The only positive integer that divides both 10 and 11 is 1. Therefore, GCD(10, 11) = 1. 10 and 11 are relatively prime or coprime meaning their GCD is 1.
-
Apply the formula: LCM(10, 11) × GCD(10, 11) = 10 × 11 LCM(10, 11) × 1 = 110 LCM(10, 11) = 110
This method confirms that the LCM of 10 and 11 is 110.
Listing Multiples: A More Intuitive (But Less Efficient) Approach
For smaller numbers, a simpler (though less efficient for larger numbers) approach is to list the multiples of each number until a common multiple is found.
Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120... Multiples of 11: 11, 22, 33, 44, 55, 66, 77, 88, 99, 110, 121...
The smallest common multiple in both lists is 110. This confirms our earlier results.
The Significance of Relatively Prime Numbers (like 10 and 11)
The fact that 10 and 11 are relatively prime (their GCD is 1) significantly simplifies the LCM calculation. When two numbers are relatively prime, their LCM is simply their product. This is because they share no common factors other than 1. This observation streamlines the calculation process considerably.
LCM in Real-World Applications
While the example of finding the LCM of 10 and 11 might seem abstract, the concept of LCM has numerous practical applications:
- Manufacturing and Production: Imagine a factory producing two different products with production cycles of 10 and 11 hours respectively. The LCM (110 hours) helps determine when both production lines will complete a cycle simultaneously.
- Scheduling and Time Management: Coordinating events or tasks that repeat at different intervals (e.g., meetings, deliveries) involves LCM calculations to find the next time all events occur simultaneously.
- Music and Rhythm: The LCM is used in music theory to determine the least common multiple of note durations, crucial for harmonizing different rhythmic patterns.
- Computer Science: Algorithms in computer science often utilize the LCM to optimize processes and manage resources efficiently.
Frequently Asked Questions (FAQ)
Q: Is there a formula for finding the LCM of more than two numbers?
A: Yes, there are methods to extend the LCM calculation to more than two numbers. One approach involves finding the LCM of the first two numbers, then finding the LCM of that result and the third number, and so on. Prime factorization remains a powerful tool for this purpose.
Q: What if the numbers are very large?
A: For very large numbers, using the Euclidean algorithm to find the GCD first and then applying the LCM-GCD relationship is generally more efficient than direct prime factorization, especially if the numbers are not easily factorable.
Q: Can the LCM of two numbers ever be smaller than the larger number?
A: No. The LCM of two numbers will always be greater than or equal to the larger of the two numbers.
Conclusion
Finding the least common multiple of 10 and 11, which is 110, might appear trivial at first glance. However, exploring the different methods—prime factorization, the GCD relationship, and listing multiples—illuminates the underlying principles of number theory and reveals the power and versatility of the LCM concept. This fundamental mathematical idea extends far beyond simple arithmetic problems and finds practical applications in various fields, underscoring its importance in both pure mathematics and real-world scenarios. Understanding the LCM is not merely about calculating a numerical value; it's about grasping a core concept that unlocks solutions to complex problems across diverse disciplines. The seemingly simple task of finding the LCM of 10 and 11 has opened a gateway to a deeper appreciation of mathematical principles and their far-reaching significance.
Latest Posts
Latest Posts
-
Rational And Irrational Number Calculator
Sep 11, 2025
-
Is 4 5 Greater Than 1 2
Sep 11, 2025
-
Gallons In A Gas Tank
Sep 11, 2025
-
110 Degrees Fahrenheit To Celsius
Sep 11, 2025
-
Write Amount In Words Cheque
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 10 And 11 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.