Is 4/5 Greater Than 1/2
saludintensiva
Sep 11, 2025 · 5 min read
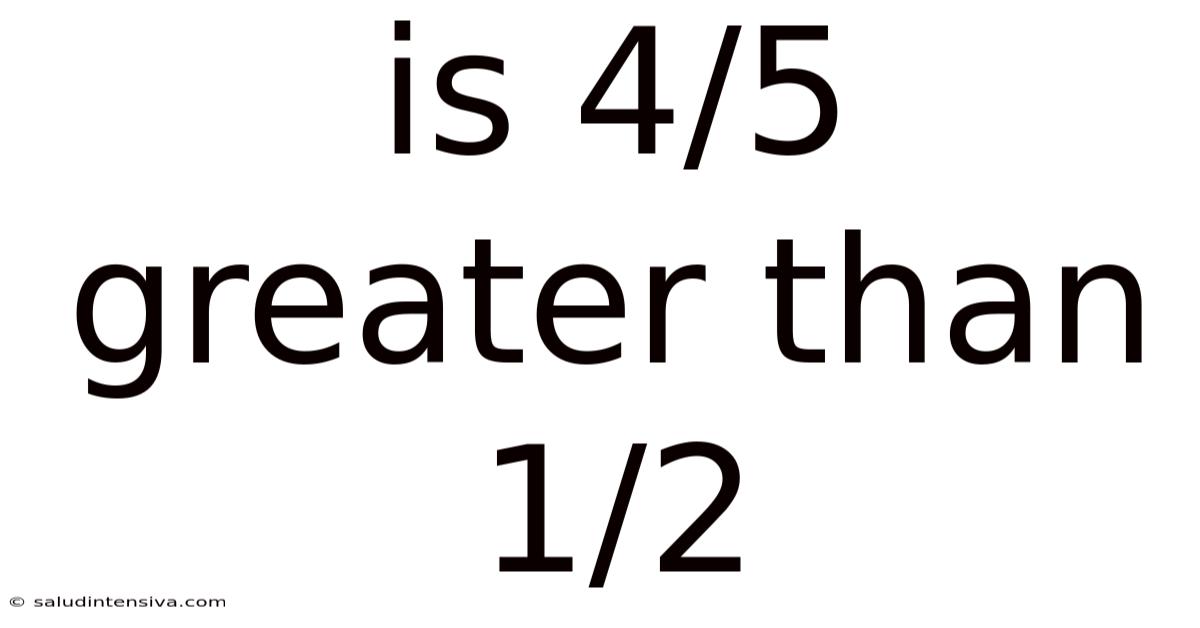
Table of Contents
Is 4/5 Greater Than 1/2? A Comprehensive Exploration of Fraction Comparison
Understanding fractions is a fundamental skill in mathematics, crucial for various applications in everyday life and advanced studies. This article will delve into the question: Is 4/5 greater than 1/2? We'll explore multiple methods for comparing fractions, explaining the concepts in a clear and accessible way, suitable for learners of all levels. We'll move beyond a simple "yes" or "no" answer, providing a deep understanding of fractional comparisons and equipping you with the tools to tackle similar problems independently.
Introduction: Understanding Fractions
Before we tackle the core question, let's refresh our understanding of fractions. A fraction represents a part of a whole. It's composed of two numbers: the numerator (the top number) and the denominator (the bottom number). The denominator tells us how many equal parts the whole is divided into, while the numerator tells us how many of those parts we're considering. For example, in the fraction 1/2, the whole is divided into two equal parts, and we're considering one of those parts.
Method 1: Visual Comparison
One of the simplest ways to compare fractions is through visual representation. Imagine two identical pizzas. For 4/5, we slice the first pizza into five equal slices and take four of them. For 1/2, we slice the second pizza into two equal slices and take one. By visually comparing the amount of pizza we have in each case, it's clear that four-fifths of a pizza is significantly larger than one-half. This visual method provides an intuitive understanding of the relative sizes of the fractions.
Method 2: Finding a Common Denominator
This method is more formal and allows for precise comparison of any two fractions. The key is to find a common denominator, which is a number that is a multiple of both denominators. Let's compare 4/5 and 1/2.
-
Find the least common multiple (LCM) of the denominators: The denominators are 5 and 2. The LCM of 5 and 2 is 10.
-
Convert the fractions to equivalent fractions with the common denominator:
- To convert 4/5 to an equivalent fraction with a denominator of 10, we multiply both the numerator and denominator by 2: (4 x 2) / (5 x 2) = 8/10
- To convert 1/2 to an equivalent fraction with a denominator of 10, we multiply both the numerator and denominator by 5: (1 x 5) / (2 x 5) = 5/10
-
Compare the numerators: Now we compare 8/10 and 5/10. Since 8 > 5, we conclude that 8/10 > 5/10, and therefore, 4/5 > 1/2.
This method provides a robust and reliable way to compare fractions, regardless of their complexity. It's particularly useful when visual comparison becomes difficult or impractical.
Method 3: Converting to Decimals
Another approach involves converting the fractions to decimals. This method is particularly helpful when dealing with fractions that are difficult to compare using common denominators.
-
Convert 4/5 to a decimal: 4/5 = 0.8
-
Convert 1/2 to a decimal: 1/2 = 0.5
-
Compare the decimals: Since 0.8 > 0.5, we conclude that 4/5 > 1/2.
This method leverages the familiarity most people have with decimal numbers, making it a relatively intuitive approach for fraction comparison.
Method 4: Using Cross-Multiplication
Cross-multiplication offers a quick and efficient way to compare two fractions. This method involves multiplying the numerator of one fraction by the denominator of the other, and vice-versa.
-
Cross-multiply:
- Multiply the numerator of 4/5 (4) by the denominator of 1/2 (2): 4 x 2 = 8
- Multiply the numerator of 1/2 (1) by the denominator of 4/5 (5): 1 x 5 = 5
-
Compare the products: Since 8 > 5, we conclude that 4/5 > 1/2.
This method eliminates the need to find a common denominator, making it a faster alternative for simple fraction comparisons.
Understanding the Magnitude of the Difference
While we've established that 4/5 is greater than 1/2, it's beneficial to understand the magnitude of this difference. The difference between 4/5 and 1/2 is:
4/5 - 1/2 = 8/10 - 5/10 = 3/10
This means 4/5 is 3/10 larger than 1/2. This understanding adds context to the comparison, highlighting the significant difference between the two fractions.
Extending the Concept: Comparing More Complex Fractions
The methods described above can be applied to compare more complex fractions. For example, let's compare 7/8 and 2/3.
Using the common denominator method:
- The LCM of 8 and 3 is 24.
- 7/8 = (7 x 3) / (8 x 3) = 21/24
- 2/3 = (2 x 8) / (3 x 8) = 16/24
- Since 21 > 16, we conclude that 7/8 > 2/3.
Frequently Asked Questions (FAQ)
-
Q: Are there any shortcuts for comparing fractions?
A: Yes, understanding fraction benchmarks (like 1/2, 1/4, 3/4) can be a shortcut. If one fraction is clearly above a benchmark and the other is below, it simplifies the comparison. Cross-multiplication is also a quick method for many comparisons.
-
Q: What if the fractions have different signs (positive and negative)?
A: Positive fractions are always greater than negative fractions. For comparing negative fractions, the fraction with the smaller absolute value (ignoring the negative sign) is the larger fraction. For example, -1/2 > -4/5.
-
Q: How can I improve my understanding of fractions?
A: Practice is key! Work through numerous examples using different comparison methods. Use visual aids like diagrams and manipulatives to build your intuition. Focus on mastering the fundamental concepts of numerators, denominators, and equivalent fractions.
Conclusion: Mastering Fraction Comparison
Comparing fractions is a fundamental mathematical skill with broad applications. This article has explored multiple methods for comparing fractions, emphasizing the importance of understanding the underlying concepts. Whether you use visual comparisons, find common denominators, convert to decimals, or employ cross-multiplication, the key is to choose the method that best suits the situation and your level of understanding. Through consistent practice and a solid grasp of the fundamentals, you can confidently compare any two fractions and build a strong foundation in mathematics. Remember, the ability to compare fractions is not just about finding the larger fraction; it's about developing a deep understanding of fractional representation and its applications in problem-solving. By mastering these techniques, you'll unlock a deeper understanding of numbers and build confidence in your mathematical abilities.
Latest Posts
Latest Posts
-
3 To The 7 Power
Sep 12, 2025
-
Gcf Of 50 And 20
Sep 12, 2025
-
15 10 As A Decimal
Sep 12, 2025
-
8276 Square Feet To Acres
Sep 12, 2025
-
Sq Ft To Km 2
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about Is 4/5 Greater Than 1/2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.