15 10 As A Decimal
saludintensiva
Sep 12, 2025 · 6 min read
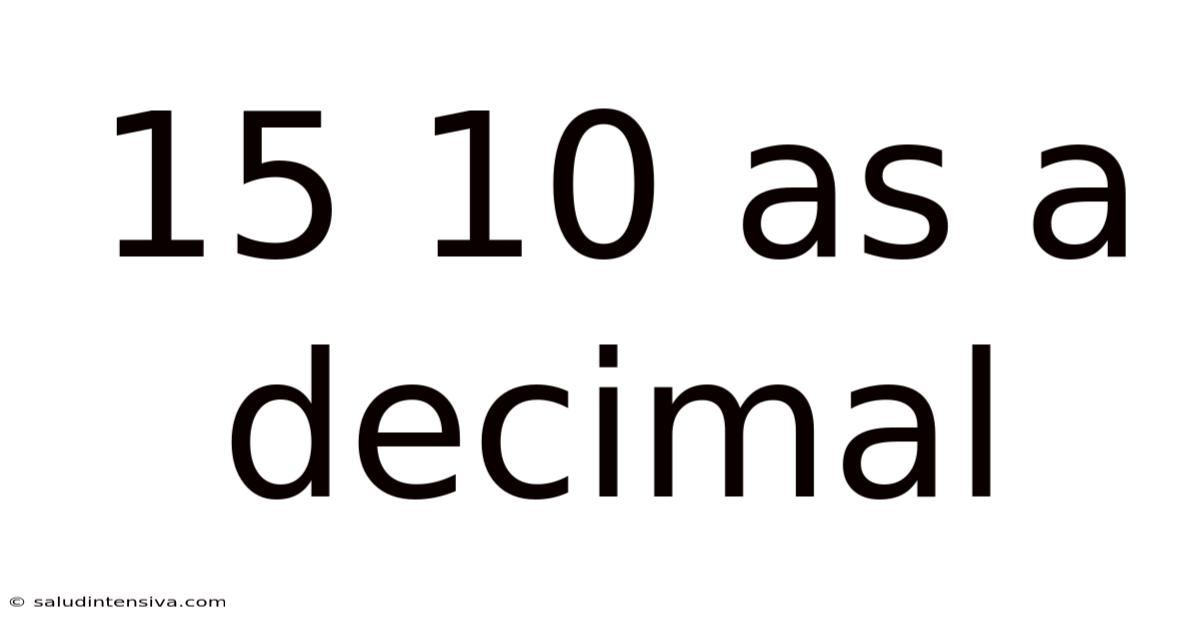
Table of Contents
Understanding 15/10 as a Decimal: A Comprehensive Guide
Fractions and decimals are fundamental concepts in mathematics, representing parts of a whole. Converting between fractions and decimals is a crucial skill applicable across numerous fields, from basic arithmetic to advanced scientific calculations. This article provides a comprehensive explanation of how to convert the fraction 15/10 into a decimal, along with exploring the underlying principles and offering practical examples. We'll delve into different methods, address common misconceptions, and equip you with the knowledge to confidently tackle similar conversions.
Introduction: Fractions and Decimals – A Brief Overview
A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For example, in the fraction 15/10, 15 is the numerator and 10 is the denominator. This means we have 15 parts out of a total of 10 parts.
A decimal is another way to represent a part of a whole, using a base-ten system. The numbers to the left of the decimal point represent whole numbers, while the numbers to the right represent fractions of a whole. For instance, 2.5 means two whole units and five-tenths of a unit.
Converting between fractions and decimals is essential for various mathematical operations and real-world applications. Understanding this conversion process allows for greater flexibility and efficiency in problem-solving.
Method 1: Direct Division
The most straightforward method to convert a fraction to a decimal is through direct division. We divide the numerator (15) by the denominator (10).
15 ÷ 10 = 1.5
Therefore, 15/10 as a decimal is 1.5. This is a simple division problem, easily solvable with a calculator or by hand.
Method 2: Simplifying the Fraction First
Before performing the division, we can often simplify the fraction to make the calculation easier. Simplifying a fraction means reducing it to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD).
In this case, the GCD of 15 and 10 is 5. Dividing both the numerator and the denominator by 5, we get:
15 ÷ 5 = 3 10 ÷ 5 = 2
This simplifies the fraction to 3/2. Now, we perform the division:
3 ÷ 2 = 1.5
This confirms that 15/10, when simplified to 3/2, also equals 1.5 as a decimal. Simplifying first can be particularly helpful when dealing with larger numbers.
Understanding the Decimal Place Value
The decimal 1.5 has two parts: the whole number part (1) and the fractional part (0.5). The digit 5 in the tenths place represents 5/10, or half (0.5). Understanding place value is crucial for interpreting and working with decimals.
- Ones place: The digit to the left of the decimal point represents the number of ones.
- Tenths place: The first digit to the right of the decimal point represents the number of tenths (1/10).
- Hundredths place: The second digit to the right of the decimal point represents the number of hundredths (1/100).
- Thousandths place: The third digit to the right of the decimal point represents the number of thousandths (1/1000), and so on.
Visual Representation: Understanding 15/10
Imagine a pizza cut into 10 equal slices. The fraction 15/10 means you have 15 slices of that pizza. Since a pizza only has 10 slices, this implies you have more than one whole pizza. You have one whole pizza (10 slices) and 5 additional slices (5/10 of a pizza). This visually represents 1.5, confirming our decimal conversion.
Converting Other Fractions to Decimals
The methods outlined above can be applied to convert any fraction to a decimal. Here are a few examples:
- 1/4: 1 ÷ 4 = 0.25
- 3/5: 3 ÷ 5 = 0.6
- 7/8: 7 ÷ 8 = 0.875
- 22/7 (approximation of Pi): 22 ÷ 7 ≈ 3.142857... (this is a recurring decimal)
Some fractions, like 22/7, result in recurring or non-terminating decimals. These decimals continue infinitely without repeating in a predictable pattern.
Common Misconceptions about Fraction to Decimal Conversion
A common mistake is incorrectly placing the decimal point. Always remember to divide the numerator by the denominator. Another mistake is forgetting to simplify the fraction before performing the division; simplifying makes the calculation easier and less prone to errors.
Practical Applications of Decimal Conversions
Converting fractions to decimals has numerous applications in everyday life and various professions. Here are some examples:
- Finance: Calculating percentages, interest rates, and discounts often involves converting fractions to decimals.
- Engineering: Precision measurements and calculations frequently use decimals.
- Science: Scientific data is often expressed using decimals.
- Cooking: Following recipes often involves converting fractions (like ½ cup) to decimals for more precise measurements.
Frequently Asked Questions (FAQ)
Q1: What if the denominator is a power of 10 (e.g., 10, 100, 1000)?
A1: If the denominator is a power of 10, converting to a decimal is particularly simple. You simply move the decimal point in the numerator to the left by the number of zeros in the denominator. For example:
- 15/10: Move the decimal point in 15 (15.0) one place to the left, resulting in 1.5.
- 125/100: Move the decimal point in 125 (125.0) two places to the left, resulting in 1.25.
- 3250/1000: Move the decimal point in 3250 (3250.0) three places to the left, resulting in 3.25.
Q2: What happens if the fraction is an improper fraction (numerator is larger than the denominator)?
A2: An improper fraction, such as 15/10, results in a decimal greater than 1. This simply means that the decimal represents a whole number and a fractional part.
Q3: Can I use a calculator to convert fractions to decimals?
A3: Yes, most calculators have a division function that can easily perform this conversion.
Q4: Are there any online tools to convert fractions to decimals?
A4: Yes, numerous websites and apps offer free fraction-to-decimal converters. These tools can be very helpful for quick conversions and checking your work.
Conclusion: Mastering Fraction to Decimal Conversions
Converting fractions to decimals is a fundamental mathematical skill with widespread applications. By understanding the underlying principles and applying the methods outlined in this article, you can confidently convert fractions to decimals, regardless of their complexity. Remember to simplify the fraction whenever possible to make the division easier and to check your work using alternative methods or calculators. Mastering this skill will significantly enhance your mathematical abilities and facilitate problem-solving in various contexts. The ability to seamlessly transition between fractions and decimals is a cornerstone of numerical literacy, empowering you to tackle more complex mathematical challenges with ease and confidence. Through practice and understanding, this seemingly simple skill becomes a powerful tool in your mathematical arsenal.
Latest Posts
Latest Posts
-
59 Degrees F To C
Sep 12, 2025
-
12 15 In The Simplest Form
Sep 12, 2025
-
Order Doesnt Matter With Replacement
Sep 12, 2025
-
50 Dollars 40 Percent Off
Sep 12, 2025
-
How To Figure Out 15
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 15 10 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.