12/15 In The Simplest Form
saludintensiva
Sep 12, 2025 · 5 min read
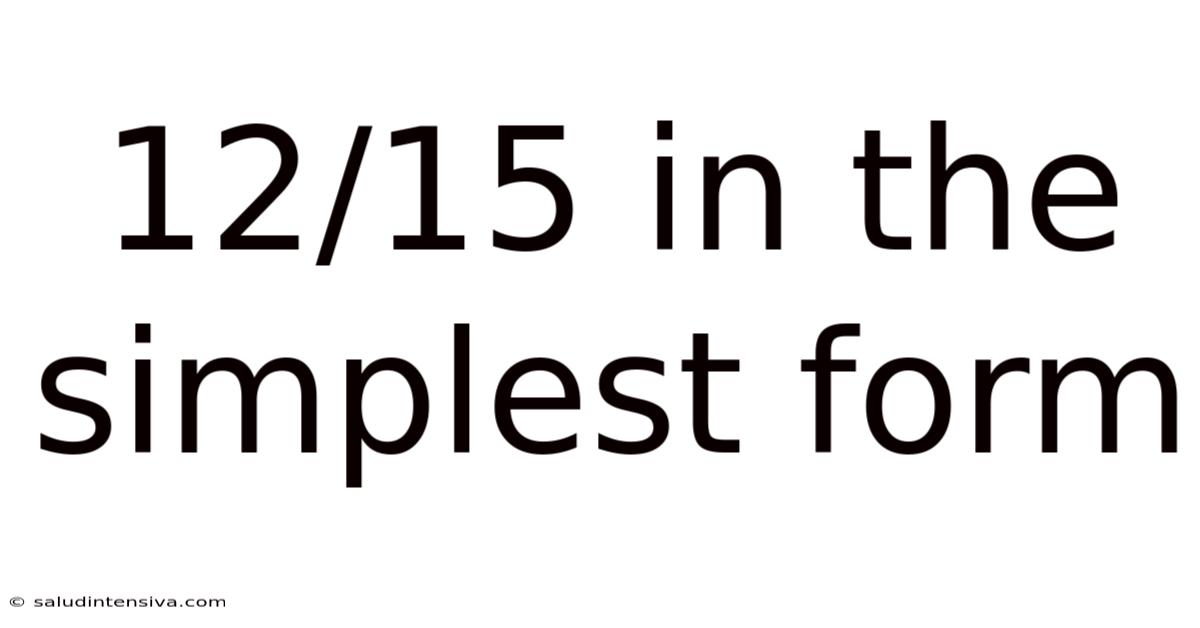
Table of Contents
Understanding Fractions: Simplifying 12/15 to its Simplest Form
Fractions are a fundamental part of mathematics, representing parts of a whole. Understanding how to simplify fractions is crucial for various mathematical operations and applications in everyday life. This article will guide you through the process of simplifying the fraction 12/15 to its simplest form, explaining the concepts involved and providing a step-by-step approach. We'll also explore the underlying mathematical principles and address common questions about fraction simplification. By the end, you'll not only know the simplest form of 12/15 but also have a solid understanding of how to simplify any fraction.
What is a Fraction?
A fraction represents a part of a whole. It's written as a ratio of two numbers, the numerator (top number) and the denominator (bottom number). The numerator indicates how many parts you have, and the denominator indicates how many parts make up the whole. For example, in the fraction 12/15, 12 is the numerator and 15 is the denominator. This means we have 12 parts out of a possible 15 parts.
Simplifying Fractions: The Concept of Greatest Common Factor (GCF)
Simplifying a fraction means reducing it to its lowest terms. This means finding an equivalent fraction where the numerator and denominator are smaller but still represent the same proportion. The key to simplifying is finding the greatest common factor (GCF) of the numerator and the denominator. The GCF is the largest number that divides both the numerator and the denominator without leaving a remainder. Once you find the GCF, you divide both the numerator and the denominator by it.
Step-by-Step Simplification of 12/15
Let's simplify 12/15 step-by-step:
-
Find the factors of the numerator (12): The factors of 12 are 1, 2, 3, 4, 6, and 12.
-
Find the factors of the denominator (15): The factors of 15 are 1, 3, 5, and 15.
-
Identify the common factors: By comparing the lists, we see that the common factors of 12 and 15 are 1 and 3.
-
Determine the greatest common factor (GCF): The largest common factor is 3. This is our GCF.
-
Divide both the numerator and the denominator by the GCF:
- 12 ÷ 3 = 4
- 15 ÷ 3 = 5
Therefore, the simplified form of 12/15 is 4/5.
Visual Representation
Imagine a pizza cut into 15 slices. You have 12 of those slices (12/15). If you group the slices into sets of 3, you'll have 4 groups of 3 slices out of 5 possible groups of 3 slices (4/5). This visual representation helps understand why 12/15 and 4/5 represent the same proportion.
Prime Factorization Method for Finding the GCF
Another method to find the GCF is using prime factorization. Prime factorization involves breaking down a number into its prime factors (numbers divisible only by 1 and themselves).
-
Prime factorization of 12: 12 = 2 x 2 x 3 = 2² x 3
-
Prime factorization of 15: 15 = 3 x 5
-
Identify common prime factors: Both 12 and 15 share the prime factor 3.
-
Calculate the GCF: The GCF is the product of the common prime factors raised to the lowest power. In this case, it's just 3 (3¹).
-
Simplify the fraction: Divide both the numerator and denominator by the GCF (3), resulting in 4/5.
This method is particularly useful for larger numbers where finding factors by inspection might be challenging.
Why Simplify Fractions?
Simplifying fractions is important for several reasons:
-
Easier calculations: Working with smaller numbers is generally easier and less prone to errors. For example, adding 4/5 and 2/5 is much simpler than adding 12/15 and 6/15.
-
Clearer understanding: Simplified fractions provide a clearer representation of the proportion. 4/5 is easier to grasp intuitively than 12/15.
-
Standardized form: Simplifying fractions ensures that you're working with a standardized form, making comparisons and calculations consistent.
-
Applications in various fields: Simplified fractions are essential in various fields like engineering, physics, and finance, where accurate calculations and clear representations are crucial.
Common Mistakes to Avoid
-
Dividing only the numerator or denominator: Remember to always divide both the numerator and the denominator by the GCF.
-
Incorrectly identifying the GCF: Carefully analyze the factors to ensure you've found the greatest common factor.
-
Not simplifying completely: Double-check your work to make sure the fraction cannot be simplified further.
Frequently Asked Questions (FAQ)
Q: Is 4/5 the only simplified form of 12/15?
A: Yes, 4/5 is the simplest form of 12/15 because the numerator and denominator have no common factors other than 1.
Q: What if the GCF is 1?
A: If the GCF of the numerator and denominator is 1, the fraction is already in its simplest form. This means there are no common factors to divide by, other than 1, which doesn't change the value of the fraction.
Q: Can I simplify fractions with negative numbers?
A: Yes. The process remains the same. Find the GCF, ignoring the negative sign, and then divide both the numerator and the denominator. The resulting fraction will retain the negative sign if either the numerator or denominator (but not both) was initially negative. For example, -12/15 simplifies to -4/5.
Q: Are there any shortcuts for simplifying fractions?
A: While prime factorization is a systematic approach, sometimes you can spot common factors quickly. If both the numerator and denominator are even, you know they share a factor of 2. If they both end in 0 or 5, they share a factor of 5. However, always double-check to ensure you've found the GCF.
Conclusion
Simplifying fractions is a crucial skill in mathematics. By understanding the concept of the greatest common factor (GCF) and following the steps outlined above, you can effectively simplify any fraction to its lowest terms. The simplification of 12/15 to 4/5 demonstrates this process clearly. Mastering fraction simplification will improve your mathematical abilities and help you navigate various real-world problems requiring a precise understanding of proportions and ratios. Remember to practice regularly to reinforce your understanding and build confidence in working with fractions. The more you practice, the easier and faster it will become.
Latest Posts
Latest Posts
-
Fraction Equivalent To 2 4
Sep 12, 2025
-
1930 Military Time To Normal
Sep 12, 2025
-
Number To Words Indian Currency
Sep 12, 2025
-
12 Out Of 15 Percent
Sep 12, 2025
-
Convert 25 F To C
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 12/15 In The Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.