12 Out Of 15 Percent
saludintensiva
Sep 12, 2025 · 6 min read
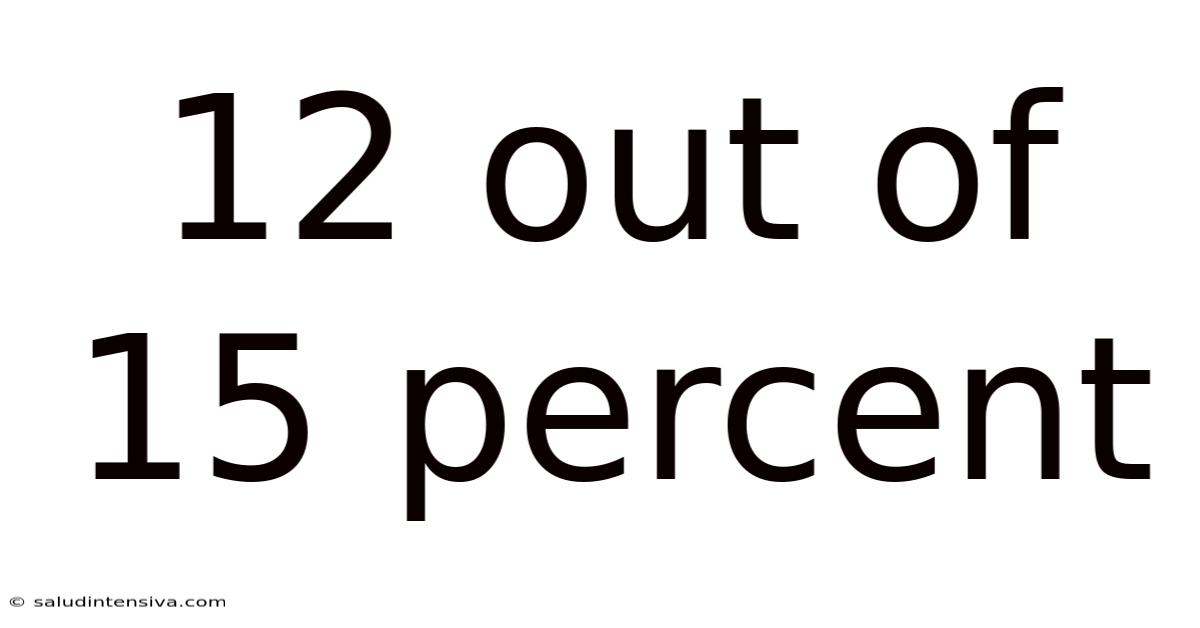
Table of Contents
Understanding 12 out of 15: A Deep Dive into Percentages, Fractions, and Ratios
Understanding percentages, fractions, and ratios is crucial in many aspects of life, from everyday budgeting and cooking to more complex fields like finance and science. This article will explore the meaning of "12 out of 15," demonstrating how to express it as a fraction, a percentage, and a ratio, and explaining the underlying mathematical concepts. We'll delve into practical applications and address frequently asked questions to provide a comprehensive understanding of this seemingly simple yet fundamentally important concept.
What does "12 out of 15" mean?
"12 out of 15" signifies that we have 12 items or parts out of a total of 15 items or parts. This phrase represents a part-to-whole relationship, where 12 is the part and 15 is the whole. Understanding this basic relationship is the cornerstone of grasping percentages, fractions, and ratios.
Expressing "12 out of 15" as a Fraction
A fraction is a way of representing a part of a whole. In this case, "12 out of 15" can be easily written as the fraction 12/15. This fraction shows that 12 is the numerator (the part) and 15 is the denominator (the whole).
This fraction, however, can be simplified. Both the numerator and denominator are divisible by 3. Dividing both by 3 gives us the equivalent fraction 4/5. This simplified fraction is easier to work with and represents the same proportion. Remember, simplifying a fraction doesn't change its value; it only makes it more manageable.
Calculating the Percentage
A percentage expresses a fraction as a portion of 100. To convert the fraction 12/15 (or its simplified form 4/5) into a percentage, we need to find an equivalent fraction with a denominator of 100.
There are two main methods for doing this:
Method 1: Using the simplified fraction
- We start with the simplified fraction 4/5.
- To get a denominator of 100, we multiply both the numerator and the denominator by 20 (since 5 x 20 = 100).
- This gives us (4 x 20) / (5 x 20) = 80/100.
- Therefore, 80/100 is equivalent to 80%. This means that 12 out of 15 represents 80%.
Method 2: Using the original fraction
- Start with the original fraction 12/15.
- Divide the numerator (12) by the denominator (15): 12 ÷ 15 = 0.8
- Multiply the decimal result by 100 to express it as a percentage: 0.8 x 100 = 80%
Both methods yield the same result: 80%. Choosing the method depends on personal preference and the complexity of the fraction. For simpler fractions, like 4/5, Method 1 is often quicker. For more complex fractions, Method 2 might be easier.
Understanding Ratios
A ratio is a comparison of two or more quantities. "12 out of 15" can be expressed as a ratio of 12:15, which reads as "12 to 15." Similar to fractions, ratios can be simplified by dividing both numbers by their greatest common divisor. In this case, the greatest common divisor of 12 and 15 is 3. Simplifying the ratio gives us 4:5. This simplified ratio still represents the same proportion as 12:15.
Real-World Applications
The concept of "12 out of 15" and its representations as a fraction, percentage, and ratio are widely applicable in various real-world scenarios:
- Academic Performance: If a student answered 12 questions correctly out of 15, their score is 80%.
- Sales Targets: A salesperson achieving 12 sales out of a target of 15 has an 80% success rate.
- Manufacturing Quality Control: If 12 out of 15 manufactured products pass quality checks, the pass rate is 80%.
- Surveys and Polling: If 12 out of 15 respondents agree with a particular statement, 80% of respondents agree.
- Recipe Scaling: If a recipe calls for 12 ounces of flour out of a total of 15 ounces of dry ingredients, flour constitutes 80% of the dry ingredients.
Further Exploration: Percentage Increase and Decrease
Understanding percentages allows us to calculate percentage increases and decreases. Imagine that the total number of items increased from 15 to 20, while the number of successful items remained at 12.
The initial percentage was 80% (12/15). The new percentage is 60% (12/20). This represents a decrease of 20 percentage points (80% - 60% = 20%). To calculate the percentage decrease relative to the original value, we would perform the following calculation: [(80-60)/80] * 100% = 25%. This means there's been a 25% decrease in the success rate.
Similarly, if the number of successful items increased from 12 to 18 while the total remained at 15, the new percentage would be 120% (18/15), indicating a 40 percentage point increase (120% - 80% = 40%). This showcases the flexibility and importance of understanding percentages in analyzing changes.
Frequently Asked Questions (FAQ)
Q: What is the simplest form of the fraction 12/15?
A: The simplest form of 12/15 is 4/5. Both the numerator and denominator are divisible by 3.
Q: Can I express "12 out of 15" as a decimal?
A: Yes, 12/15 simplifies to 4/5, which is equivalent to 0.8 as a decimal.
Q: How do I convert a percentage back to a fraction?
A: To convert a percentage to a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, 80% becomes 80/100, which simplifies to 4/5.
Q: What is the difference between a ratio and a fraction?
A: While both ratios and fractions represent a part-to-whole relationship, ratios can compare more than two quantities, while fractions typically represent a single part to the whole. However, they are closely related and often interchangeable in representing proportions.
Q: How can I improve my understanding of percentages, fractions, and ratios?
A: Practice is key. Solve various problems involving percentages, fractions, and ratios. Use online calculators and resources for practice and verification. Break down complex problems into smaller, manageable steps.
Conclusion
Understanding "12 out of 15," its representation as a fraction (4/5), percentage (80%), and ratio (4:5), is crucial for navigating numerous everyday situations and more advanced mathematical concepts. The ability to convert between these forms and to apply them in practical contexts is a valuable skill applicable across various disciplines. By mastering these fundamental concepts, you equip yourself with a powerful tool for understanding and analyzing proportions and relationships in the world around you. Remember to practice consistently to solidify your understanding and build confidence in your mathematical abilities.
Latest Posts
Latest Posts
-
Date For 21 Year Olds
Sep 12, 2025
-
4 5 As A Percent
Sep 12, 2025
-
Convert 23 To A Decimal
Sep 12, 2025
-
Absolute Value Of A Decimal
Sep 12, 2025
-
Convert 15 Into A Decimal
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 12 Out Of 15 Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.