10 15 In Simplest Form
saludintensiva
Sep 25, 2025 · 6 min read
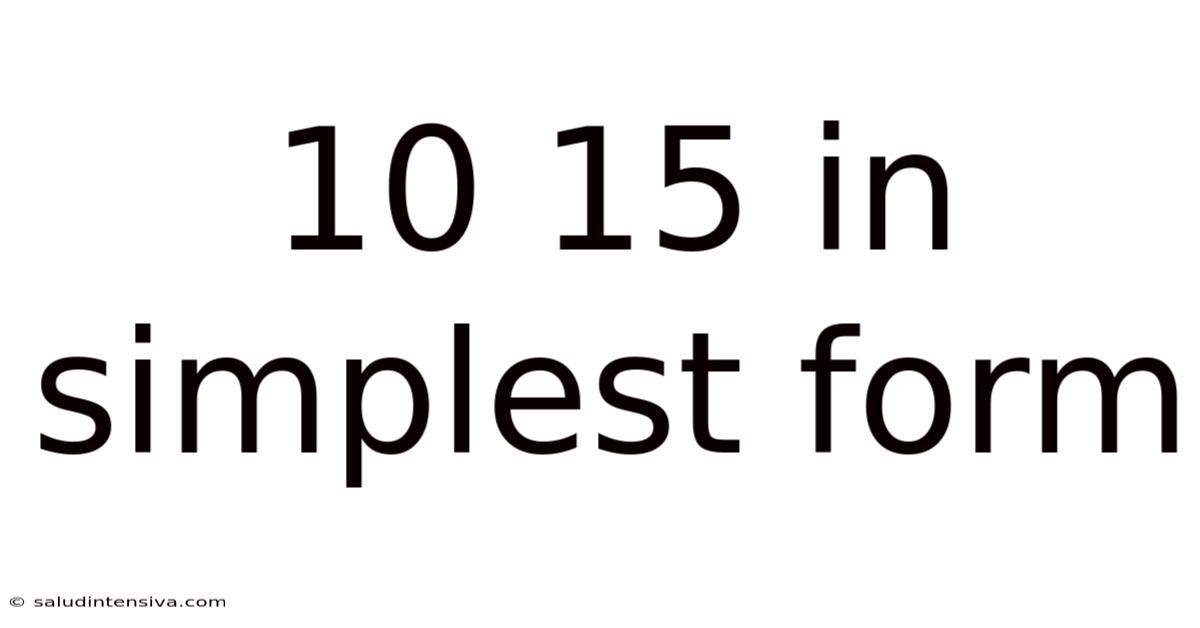
Table of Contents
Simplifying Fractions: A Deep Dive into 10/15
Understanding fractions is a fundamental building block in mathematics. This article will explore the simplification of fractions, using the example of 10/15, and delve into the underlying concepts to provide a thorough understanding for students of all levels. We'll cover the process, the mathematical reasoning behind it, and even address common questions and misconceptions. By the end, you'll not only know the simplest form of 10/15 but also possess a robust understanding of fraction simplification.
Introduction: What is Fraction Simplification?
A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). Fraction simplification, also known as reducing fractions or expressing fractions in their lowest terms, is the process of finding an equivalent fraction with a smaller numerator and denominator. This doesn't change the value of the fraction; it just represents it in a more concise and manageable form. Think of it like simplifying a recipe – you can halve all the ingredients and still get the same dish. Our goal with 10/15 is to find the simplest equivalent fraction.
Understanding Equivalent Fractions
Before diving into simplifying 10/15, let's understand the concept of equivalent fractions. Equivalent fractions represent the same value even though they look different. For example, 1/2, 2/4, 3/6, and 4/8 are all equivalent fractions because they all represent one-half. We obtain equivalent fractions by multiplying or dividing both the numerator and the denominator by the same non-zero number. This is crucial – you must perform the same operation on both parts of the fraction to maintain its value.
Step-by-Step Simplification of 10/15
Now let's simplify 10/15. The key is to find the greatest common divisor (GCD) or highest common factor (HCF) of the numerator (10) and the denominator (15). The GCD is the largest number that divides both 10 and 15 without leaving a remainder.
- Find the factors of 10: The factors of 10 are 1, 2, 5, and 10.
- Find the factors of 15: The factors of 15 are 1, 3, 5, and 15.
- Identify the common factors: Both 10 and 15 share the factors 1 and 5.
- Determine the greatest common factor (GCD): The largest common factor is 5.
Now, we divide both the numerator and the denominator of 10/15 by the GCD, which is 5:
10 ÷ 5 = 2 15 ÷ 5 = 3
Therefore, the simplified form of 10/15 is 2/3.
Alternative Methods for Finding the GCD
While the method above works well for smaller numbers, finding the GCD of larger numbers can be more challenging. Here are two alternative methods:
-
Prime Factorization: This method involves breaking down the numbers into their prime factors. A prime number is a number greater than 1 that has only two factors: 1 and itself (e.g., 2, 3, 5, 7, 11).
- Prime factorization of 10: 2 x 5
- Prime factorization of 15: 3 x 5
The common prime factor is 5. Therefore, the GCD is 5.
-
Euclidean Algorithm: This is a more efficient method for larger numbers. It involves repeatedly applying the division algorithm until the remainder is 0. The last non-zero remainder is the GCD.
- Divide the larger number (15) by the smaller number (10): 15 ÷ 10 = 1 with a remainder of 5.
- Replace the larger number with the smaller number (10) and the smaller number with the remainder (5): 10 ÷ 5 = 2 with a remainder of 0.
- Since the remainder is 0, the GCD is the last non-zero remainder, which is 5.
The Mathematical Reasoning Behind Simplification
Simplifying a fraction doesn't change its value because we're essentially multiplying the fraction by 1. When we divide both the numerator and the denominator by the GCD, we are, in effect, multiplying the fraction by a fraction equivalent to 1 (e.g., 5/5 = 1).
(10/15) x (5/5) = (10 x 5) / (15 x 5) = 50/75
Notice that 50/75 can also be simplified to 2/3 by dividing both the numerator and denominator by 25. The simplification using the GCD directly avoids these extra steps.
Beyond 10/15: Applying the Process to Other Fractions
The process of simplifying fractions using the GCD remains the same regardless of the numbers involved. Let's consider a few examples:
- 12/18: The GCD of 12 and 18 is 6. 12 ÷ 6 = 2, and 18 ÷ 6 = 3. Therefore, 12/18 simplifies to 2/3.
- 24/36: The GCD of 24 and 36 is 12. 24 ÷ 12 = 2, and 36 ÷ 12 = 3. Therefore, 24/36 simplifies to 2/3.
- 35/49: The GCD of 35 and 49 is 7. 35 ÷ 7 = 5, and 49 ÷ 7 = 7. Therefore, 35/49 simplifies to 5/7.
Observe that even though the initial fractions are different, they can sometimes simplify to the same simplest form.
Common Mistakes and Misconceptions
- Dividing only the numerator or denominator: Remember, you must divide both the numerator and the denominator by the GCD to maintain the value of the fraction.
- Using an incorrect common factor: Always aim for the greatest common factor. Using a smaller common factor will require further simplification steps.
- Not simplifying completely: Ensure that the resulting fraction cannot be simplified further.
Frequently Asked Questions (FAQ)
-
Q: What if the numerator is 1? Is the fraction already in its simplest form?
A: Yes, if the numerator is 1, the fraction is already in its simplest form because 1 is only divisible by 1.
-
Q: What if the numerator and denominator are the same?
A: If the numerator and denominator are the same, the fraction simplifies to 1 (e.g., 5/5 = 1).
-
Q: Is there a limit to how many times I can simplify a fraction?
A: No, however, you will always arrive at the same simplest form, regardless of the order or method used to simplify.
-
Q: Can I simplify a fraction with a negative number?
A: Yes. Simplify the numerical part as described, and retain the negative sign. For example, -10/15 simplifies to -2/3.
Conclusion: Mastering Fraction Simplification
Simplifying fractions is a crucial skill in mathematics. The ability to express fractions in their simplest form makes calculations easier and improves understanding. By understanding the concepts of equivalent fractions, greatest common divisors, and the underlying mathematical reasoning, you can confidently simplify any fraction, including 10/15, which simplifies to the elegant and concise form of 2/3. Remember the steps, practice consistently, and you'll master this essential mathematical skill. This understanding will serve as a strong foundation for more advanced mathematical concepts in the future. So keep practicing, and you'll soon find simplifying fractions second nature!
Latest Posts
Latest Posts
-
2 To Power Of 2
Sep 25, 2025
-
2130 Military Time To Normal
Sep 25, 2025
-
How To Figure Class Average
Sep 25, 2025
-
Characteristic Equation Of A Matrix
Sep 25, 2025
-
Queen Of Hearts Playing Card
Sep 25, 2025
Related Post
Thank you for visiting our website which covers about 10 15 In Simplest Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.