10/9 As A Mixed Number
saludintensiva
Sep 16, 2025 · 6 min read
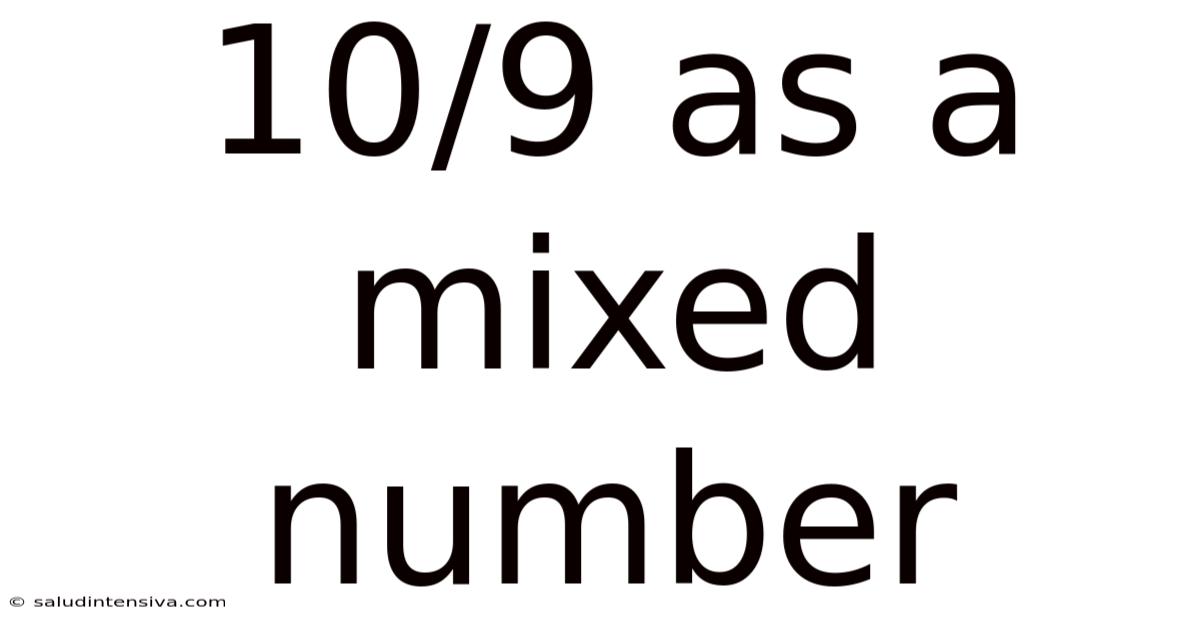
Table of Contents
Understanding 10/9 as a Mixed Number: A Comprehensive Guide
The fraction 10/9 represents a value greater than one. Understanding how to convert improper fractions like 10/9 into mixed numbers is a fundamental skill in arithmetic. This comprehensive guide will not only show you how to convert 10/9 to a mixed number but also delve into the underlying principles, provide practical examples, and address frequently asked questions. We'll explore the concept thoroughly, ensuring you gain a firm grasp of this important mathematical concept.
Introduction to Fractions and Mixed Numbers
Before diving into the conversion of 10/9, let's establish a solid foundation. A fraction represents a part of a whole. It consists of two parts: the numerator (the top number) and the denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, while the numerator shows how many of those parts are being considered.
An improper fraction is a fraction where the numerator is greater than or equal to the denominator (e.g., 10/9, 7/4, 5/5). This indicates that the fraction represents a value greater than or equal to one.
A mixed number combines a whole number and a proper fraction. A proper fraction has a numerator smaller than the denominator (e.g., 1/2, 3/4, 2/5). Mixed numbers provide a more intuitive way to represent values greater than one. For example, 1 ½ represents one whole and one-half.
Converting 10/9 to a Mixed Number: Step-by-Step
Converting an improper fraction like 10/9 to a mixed number involves dividing the numerator by the denominator. Here's a step-by-step guide:
-
Divide the numerator by the denominator: Divide 10 by 9. This gives us a quotient of 1 and a remainder of 1.
-
Write the quotient as the whole number: The quotient (1) becomes the whole number part of our mixed number.
-
Write the remainder as the numerator of the fraction: The remainder (1) becomes the numerator of the fraction part of our mixed number.
-
Keep the original denominator: The denominator (9) remains unchanged.
Therefore, 10/9 as a mixed number is 1 1/9.
Visual Representation
Imagine you have 10 slices of pizza, and each pizza is cut into 9 slices. You can clearly see that you have more than one whole pizza. You have one complete pizza (9 slices) and one slice remaining out of nine. This perfectly illustrates the mixed number 1 1/9.
Further Examples: Applying the Conversion Process
Let's practice converting other improper fractions to mixed numbers to solidify your understanding:
-
14/5: 14 ÷ 5 = 2 with a remainder of 4. Therefore, 14/5 = 2 4/5.
-
22/7: 22 ÷ 7 = 3 with a remainder of 1. Therefore, 22/7 = 3 1/7.
-
9/3: 9 ÷ 3 = 3 with a remainder of 0. This means there's no fractional part. Therefore, 9/3 = 3. (Note: This is a special case where the improper fraction simplifies to a whole number).
The Importance of Mixed Numbers
Mixed numbers offer several advantages over improper fractions:
-
Intuitive Representation: They provide a more easily understood representation of quantities greater than one. It's much clearer to visualize 1 1/9 pizzas than 10/9 pizzas.
-
Ease of Comparison: Comparing mixed numbers is often easier than comparing improper fractions. For example, comparing 2 1/3 and 1 2/3 is more straightforward than comparing 7/3 and 5/3.
-
Real-World Applications: Mixed numbers are commonly used in everyday situations, such as measuring ingredients in recipes (1 ½ cups of flour) or expressing distances (2 ¼ miles).
Converting Mixed Numbers Back to Improper Fractions
It's also crucial to understand how to convert a mixed number back into an improper fraction. This involves the following steps:
-
Multiply the whole number by the denominator: For example, with 1 1/9, multiply 1 (whole number) by 9 (denominator). This gives us 9.
-
Add the numerator to the result: Add the numerator (1) to the result from step 1 (9). This gives us 10.
-
Keep the original denominator: The denominator (9) remains unchanged.
Therefore, 1 1/9 converted back to an improper fraction is 10/9. This demonstrates the reversibility of the conversion process.
Working with Mixed Numbers in Arithmetic Operations
Adding, subtracting, multiplying, and dividing mixed numbers requires understanding of the rules of fraction arithmetic. Generally, it's easier to convert mixed numbers into improper fractions before performing these operations. For example:
-
Addition: To add 1 1/9 and 2 1/3, first convert them to improper fractions (10/9 and 7/3), find a common denominator (9), and then add: (10/9) + (21/9) = 31/9 which can be simplified to 3 4/9.
-
Subtraction: Follow a similar process to addition, converting to improper fractions and finding a common denominator before subtracting.
-
Multiplication and Division: While possible to directly multiply and divide mixed numbers, it's usually simpler to first convert them into improper fractions before performing the operation.
Frequently Asked Questions (FAQ)
Q1: Why is it important to learn about converting fractions to mixed numbers?
A1: Converting between improper fractions and mixed numbers is a fundamental skill in arithmetic. It allows for a more intuitive understanding and easier manipulation of fractions, especially when dealing with values greater than one. It's essential for solving real-world problems and progressing to more advanced mathematical concepts.
Q2: Can all improper fractions be converted into mixed numbers?
A2: Yes, all improper fractions can be converted into either a mixed number or a whole number. If the numerator is a multiple of the denominator, the result will be a whole number. Otherwise, it will be a mixed number.
Q3: What if I get a remainder of zero when dividing the numerator by the denominator?
A3: If you get a remainder of zero, it means the improper fraction is equivalent to a whole number. The quotient is the whole number representation of the fraction.
Q4: Is it always better to work with mixed numbers rather than improper fractions?
A4: While mixed numbers offer better intuitive understanding for representing quantities, improper fractions are often easier to manipulate algebraically, particularly in more advanced mathematics. The choice depends on the context and the operation being performed.
Q5: Are there any shortcuts for converting improper fractions to mixed numbers?
A5: While the step-by-step method is thorough and ensures understanding, with practice, you can often perform the division and conversion mentally, especially for simpler fractions.
Conclusion
Converting the improper fraction 10/9 to the mixed number 1 1/9 is a straightforward process involving division and understanding the concept of whole numbers and fractions. This guide has provided a detailed explanation of the process, illustrated it with examples, and explored the significance of mixed numbers in arithmetic. Mastering this fundamental skill is crucial for progressing to more complex mathematical concepts and solving real-world problems involving fractions. Remember to practice regularly to build confidence and proficiency in handling fractions and mixed numbers.
Latest Posts
Latest Posts
-
Area Of A Pipe Formula
Sep 16, 2025
-
Subtracting Fractions With Negative Numbers
Sep 16, 2025
-
Is 6 8 Equivalent To 9 12
Sep 16, 2025
-
17 Degrees C In F
Sep 16, 2025
-
Lcm Of 15 And 30
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about 10/9 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.