10 Out Of 16 Percentage
saludintensiva
Sep 17, 2025 · 5 min read
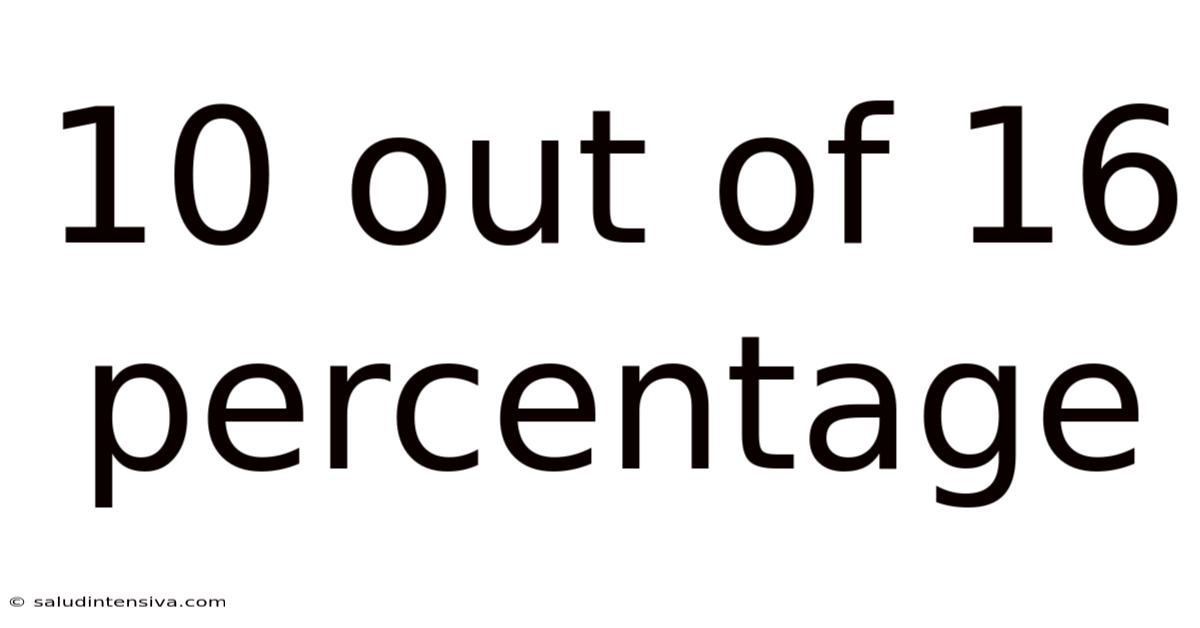
Table of Contents
Understanding 10 out of 16: Percentages, Fractions, and Real-World Applications
Understanding how to calculate and interpret percentages is a fundamental skill applicable across numerous aspects of life, from academic assessments to financial planning. This article delves into the specifics of calculating the percentage represented by "10 out of 16," exploring various methods, clarifying common misconceptions, and demonstrating its real-world relevance. We'll cover the core mathematical concepts, provide practical examples, and address frequently asked questions to ensure a comprehensive understanding of this seemingly simple yet vital concept.
Defining the Problem: 10 out of 16
The phrase "10 out of 16" represents a fraction or a ratio. It means that out of a total of 16 items or possibilities, 10 possess a specific characteristic or meet a particular criterion. To understand its significance, we need to convert this fraction into a percentage. A percentage is simply a fraction expressed as a portion of 100. This conversion allows for easier comparison and interpretation of different proportions.
Method 1: Converting the Fraction to a Percentage
The most straightforward method involves converting the fraction 10/16 into a percentage. Here's a step-by-step guide:
-
Express the ratio as a fraction: The given information is already in fractional form: 10/16.
-
Convert the fraction to a decimal: Divide the numerator (10) by the denominator (16): 10 ÷ 16 = 0.625
-
Convert the decimal to a percentage: Multiply the decimal by 100 and add the "%" symbol: 0.625 x 100 = 62.5%
Therefore, 10 out of 16 represents 62.5%.
Method 2: Using Proportions
Another approach involves using proportions to solve the problem. This method is particularly useful for visualizing the relationship between the parts and the whole.
-
Set up a proportion: We can set up a proportion to find the equivalent percentage:
10/16 = x/100
Where 'x' represents the percentage we want to find.
-
Cross-multiply: Cross-multiply the terms in the proportion:
16x = 1000
-
Solve for x: Divide both sides by 16:
x = 1000 ÷ 16 = 62.5
Therefore, x = 62.5%.
Simplifying the Fraction (Optional)
Before converting to a percentage, it's often helpful to simplify the fraction. This simplifies the division process and can provide a better understanding of the underlying ratio. Both 10 and 16 are divisible by 2, so we can simplify the fraction as follows:
10/16 = 5/8
Now, we can convert 5/8 to a decimal: 5 ÷ 8 = 0.625
And then to a percentage: 0.625 x 100 = 62.5%
Simplifying first doesn't change the final answer but makes the calculation easier.
Real-World Applications of Percentages
The ability to calculate percentages is crucial in many everyday situations:
-
Academic Performance: Imagine a student scoring 10 out of 16 on a quiz. Knowing that this equates to 62.5% allows them to understand their performance relative to the total possible marks and identify areas for improvement.
-
Financial Calculations: Percentages are fundamental in finance. Calculating interest rates, discounts, taxes, and profit margins all require an understanding of percentage calculations. For example, a 62.5% discount on a $100 item would mean a saving of $62.50.
-
Data Analysis: In statistics and data analysis, percentages are used to represent proportions within datasets. Understanding percentages is essential for interpreting charts, graphs, and reports. For example, 62.5% of respondents in a survey might agree with a particular statement.
-
Probability and Statistics: In probability, percentages are used to express the likelihood of an event occurring. If there's a 62.5% chance of rain, it implies a fairly high probability of precipitation.
-
Recipe Scaling: In cooking, adjusting recipes often involves scaling up or down using percentages. If a recipe calls for 16 ounces of flour, and you only want to make 62.5% of the recipe, you would need 10 ounces (16 * 0.625 = 10).
Common Misconceptions about Percentages
Several common misunderstandings surround percentages:
-
Confusion with Decimals: Some individuals struggle to differentiate between decimals and percentages. Remember that a percentage is a fraction out of 100, while a decimal is a representation of a part of a whole.
-
Incorrect Calculation Methods: Incorrectly applying the formula or making errors in the calculation process can lead to inaccurate results. Always double-check your work to ensure accuracy.
-
Misinterpretation of Context: The meaning of a percentage depends heavily on the context. A 62.5% increase is different from a 62.5% decrease. Understanding the context is paramount for correct interpretation.
-
Over-reliance on Calculators: While calculators are helpful, it's important to understand the underlying mathematical principles. Over-reliance on calculators without comprehension can hinder understanding.
Frequently Asked Questions (FAQ)
Q: How do I calculate the percentage increase or decrease from a base value?
A: To calculate a percentage increase or decrease, first find the difference between the new and original values. Then, divide the difference by the original value and multiply by 100. For example, if a value increases from 16 to 26, the percentage increase is: (26-16)/16 * 100 = 62.5%.
Q: What if I have a more complex ratio, such as 15 out of 24?
A: Follow the same method: 15/24 = 0.625, which is equal to 62.5%. The principle remains the same, regardless of the specific numbers involved.
Q: Are there online tools or calculators to help with percentage calculations?
A: Yes, many online tools and calculators are available for percentage calculations. These can be helpful for checking your work or for more complex calculations. However, it's crucial to understand the underlying principles even when using such tools.
Q: Why is understanding percentages important in daily life?
A: Understanding percentages is essential for making informed decisions in various areas, from financial planning and budgeting to understanding statistical data and interpreting information presented in the media.
Conclusion: Mastering Percentage Calculations
Understanding how to calculate and interpret percentages is a valuable skill with broad applicability. This article has explored the various methods for calculating the percentage equivalent of "10 out of 16," highlighting the importance of understanding both the mathematical process and the real-world implications. By mastering this fundamental skill, you'll enhance your ability to analyze data, make informed decisions, and navigate various aspects of daily life more effectively. Remember to practice regularly and apply your knowledge in different contexts to solidify your understanding and improve your proficiency in percentage calculations. The ability to confidently work with percentages will serve you well in your academic pursuits, professional endeavors, and personal life.
Latest Posts
Latest Posts
-
What Is 1 3 Of 1 5
Sep 17, 2025
-
2030 Military Time To Normal
Sep 17, 2025
-
3 5 As An Improper Fraction
Sep 17, 2025
-
9 10 Into A Decimal
Sep 17, 2025
-
Is 29 Prime Or Composite
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about 10 Out Of 16 Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.