10 Tens Is Equal To
saludintensiva
Sep 20, 2025 · 5 min read
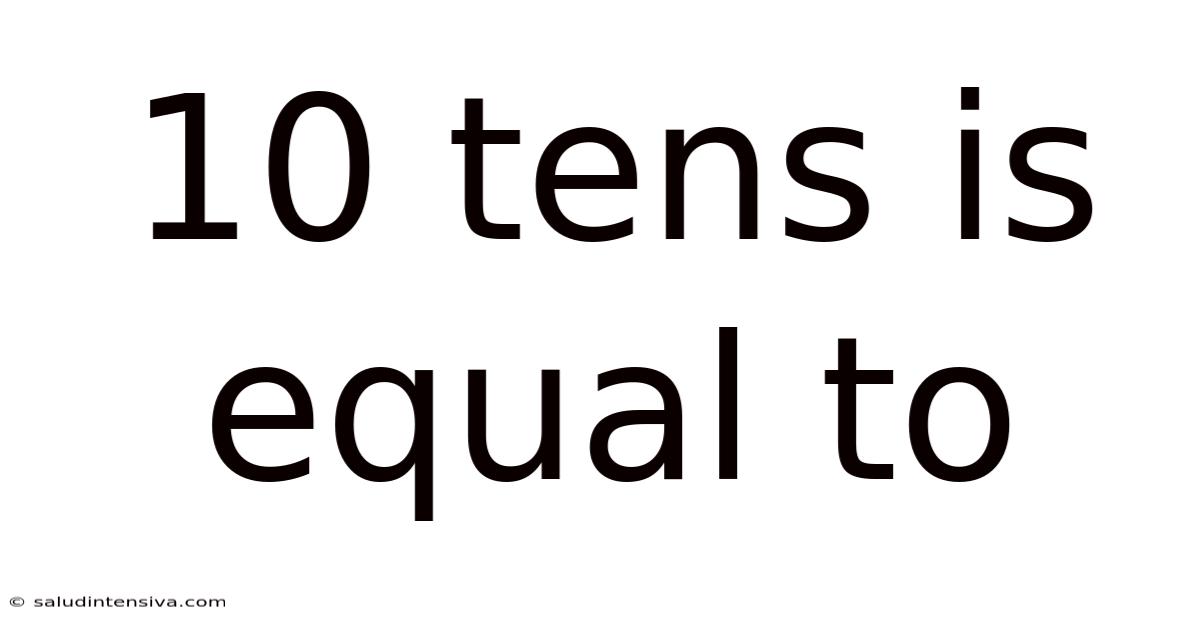
Table of Contents
10 Tens is Equal To: Understanding Place Value and its Implications
Understanding basic arithmetic is fundamental to grasping more complex mathematical concepts. This article delves into the seemingly simple question: "10 tens is equal to what?" We'll explore this concept in depth, explaining its significance in understanding place value, its practical applications, and how it lays the groundwork for more advanced mathematical operations. This exploration goes beyond a simple answer, providing a robust understanding of the underlying principles.
Introduction: Deconstructing the Basics
The statement "10 tens is equal to" might seem trivial at first glance. However, it's a cornerstone of understanding the decimal number system, a system we use daily without much conscious thought. The question touches upon the core concept of place value, the fundamental principle that determines the value of a digit based on its position within a number. This understanding is crucial not only for basic arithmetic but also for advanced mathematics, including algebra, calculus, and beyond.
The decimal system, also known as base-10, is based on the number 10. This means that each place value is ten times greater than the place value to its right. Understanding this relationship is key to solving the problem and understanding similar problems. We'll break down this relationship systematically, moving from the units place to the tens, hundreds, and beyond.
Understanding Place Value: The Foundation of the Decimal System
The decimal system is built on the concept of place value. Each digit in a number holds a specific value depending on its position. Consider the number 123:
- 3 represents 3 units or ones (3 x 1 = 3)
- 2 represents 2 tens (2 x 10 = 20)
- 1 represents 1 hundred (1 x 100 = 100)
The value of the number is the sum of the values of each digit: 100 + 20 + 3 = 123. This system is incredibly efficient and allows us to represent large numbers concisely.
Solving the Problem: 10 Tens
Now, let's address the core question: "10 tens is equal to?" We know that one ten is equal to 10 (1 x 10 = 10). Therefore, ten tens is simply 10 multiplied by 10:
10 tens = 10 x 10 = 100
Therefore, 10 tens is equal to 100. This seemingly simple equation highlights the power of place value. We've moved from the tens column to the hundreds column. This transition is fundamental to understanding how the decimal system works.
Visualizing Place Value: Using Manipulatives
Understanding place value can be made more concrete using visual aids. Imagine using base-10 blocks:
- Units: Small cubes represent individual units (ones).
- Tens: Rods composed of 10 units represent tens.
- Hundreds: Flat squares composed of 100 units represent hundreds.
To represent 10 tens, you would have 10 rods. If you group these 10 rods together, you'll see they form a square, representing one hundred. This visual representation reinforces the concept that 10 tens equal 100.
Expanding the Concept: Beyond Hundreds
The principle extends beyond hundreds. Consider:
- 10 hundreds = 1000 (one thousand)
- 10 thousands = 10,000 (ten thousand)
- 10 ten thousands = 100,000 (one hundred thousand)
Each time we multiply by 10, we move to the next higher place value. This consistent pattern is what makes the decimal system so effective for representing numbers of any magnitude.
Practical Applications: Real-World Examples
Understanding place value and the concept of "10 tens is equal to 100" has numerous practical applications in daily life:
- Money: Counting money involves understanding place value. 10 dimes (tens) make a dollar (one hundred).
- Measurement: Measuring lengths, weights, or volumes often involves working with tens, hundreds, and thousands.
- Data Analysis: Interpreting data often requires understanding place value to accurately represent and analyze information.
- Everyday calculations: Simple calculations, like grocery shopping or calculating distances, frequently rely on place value understanding.
The Importance of Place Value in Advanced Mathematics
The understanding of place value, as demonstrated by the simple equation "10 tens is equal to 100", is not just important for elementary arithmetic. It forms the bedrock of more advanced mathematical concepts:
- Algebra: Understanding place value allows us to manipulate variables and equations more efficiently.
- Calculus: Place value is implicitly used in various calculations involving limits and derivatives.
- Number Systems: The principle extends to other number systems, like binary (base-2) used in computer science, although the base changes.
Addressing Common Misconceptions
A common misconception is that understanding place value is only relevant for young learners. However, a firm grasp of place value is beneficial throughout life, from managing personal finances to comprehending complex data. A strong foundation in place value improves problem-solving skills and mathematical fluency in general. Another misconception involves confusing place value with the value of a digit. The place determines the magnitude of the digit's value, not the digit itself.
Frequently Asked Questions (FAQ)
Q: What if we had a different number system, not base-10?
A: The concept of place value still applies, but the base number changes. For example, in base-2 (binary), 10 two's is equal to 100 (in binary), which is 4 in decimal. The fundamental principle remains the same: a fixed number of units in a given place value forms a unit in the next higher place value.
Q: How does this relate to multiplication?
A: The statement "10 tens is equal to 100" is essentially a multiplication problem (10 x 10 = 100). Understanding place value provides a visual and conceptual understanding of what multiplication means in this context.
Q: Why is this concept so crucial in education?
A: A strong understanding of place value is fundamental to building a strong mathematical foundation. It lays the groundwork for all subsequent mathematical learning and problem-solving. A weak foundation in place value can lead to difficulties in more advanced mathematics.
Conclusion: The Enduring Significance of Place Value
The seemingly simple question, "10 tens is equal to," opens a gateway to a deeper understanding of the decimal number system and the crucial role of place value. This concept isn't just about memorizing facts; it's about grasping a fundamental principle that underpins all mathematical operations. From basic arithmetic to advanced calculus, the principle of place value remains consistently relevant. By reinforcing this understanding, we empower individuals with a strong mathematical foundation, enhancing their problem-solving skills and preparing them for success in various academic and real-world endeavors. Mastering this concept is an investment in lifelong learning and numerical fluency.
Latest Posts
Latest Posts
-
23 100 As A Percent
Sep 20, 2025
-
Lcm Of 4 And 2
Sep 20, 2025
-
11 2 Divided By 3
Sep 20, 2025
-
How Many Hours In Ayear
Sep 20, 2025
-
Simplify 8x 9x Completely
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about 10 Tens Is Equal To . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.