Simplify 8x - 9x Completely
saludintensiva
Sep 20, 2025 · 5 min read
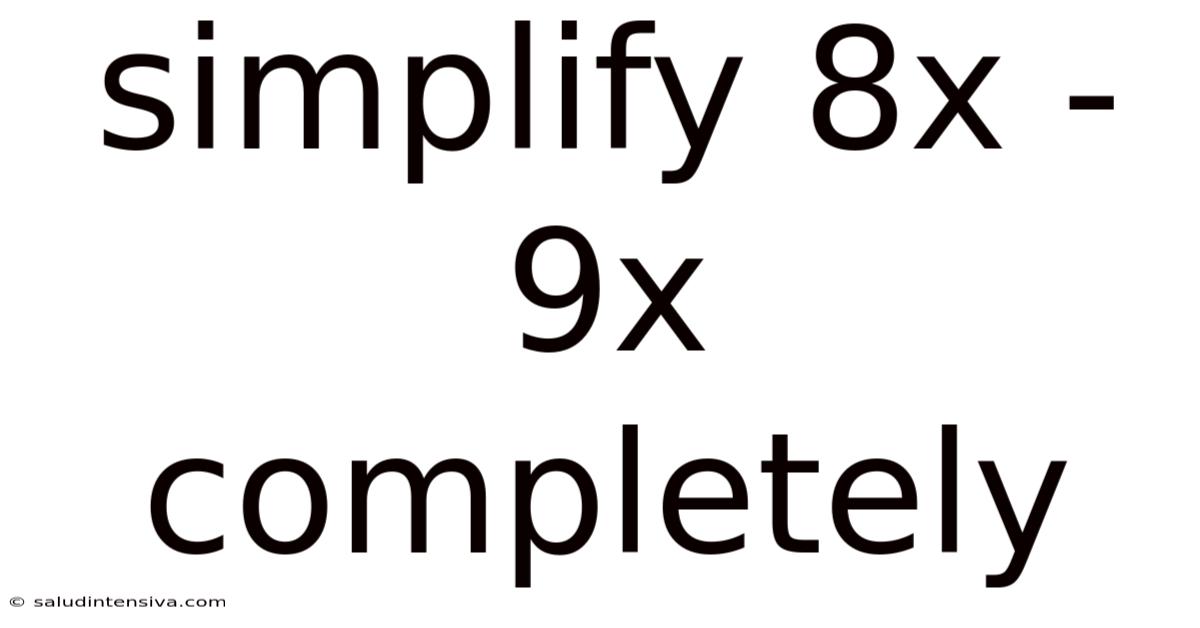
Table of Contents
Simplifying Algebraic Expressions: A Deep Dive into 8x - 9x
Simplifying algebraic expressions is a fundamental skill in mathematics, crucial for solving equations, understanding functions, and tackling more advanced topics. This article will delve into the seemingly simple expression 8x - 9x, explaining not just the solution but the underlying principles and broader applications. We will explore the concepts of like terms, coefficients, variables, and how these elements interact within algebraic expressions. By the end, you'll not only understand how to simplify 8x - 9x but also possess a solid foundation for simplifying more complex algebraic expressions.
Understanding the Components: Variables and Coefficients
Before we tackle the simplification, let's define the key components of the expression 8x - 9x. The expression consists of:
-
Variables: The 'x' in both terms is a variable. A variable represents an unknown quantity or a value that can change. Think of it as a placeholder for a number.
-
Coefficients: The '8' and '9' are coefficients. A coefficient is the numerical factor multiplying a variable. It tells us how many of the variable we have.
-
Terms: 8x and 9x are individual terms. A term is a single number, variable, or the product of numbers and variables.
-
Operation: The '-' symbol represents subtraction, indicating the operation between the two terms.
Simplifying 8x - 9x: Combining Like Terms
The core principle behind simplifying algebraic expressions is combining like terms. Like terms are terms that have the same variable raised to the same power. In our expression, 8x and 9x are like terms because they both contain the variable 'x' raised to the power of 1 (remember, x¹ is the same as x).
To simplify 8x - 9x, we focus on the coefficients: 8 and -9. We perform the indicated operation (subtraction) on these coefficients:
8 - 9 = -1
Therefore, the simplified expression is -1x, which is more commonly written as -x.
Therefore, 8x - 9x = -x
Visualizing the Simplification
Imagine you have 8 apples (8x) and you take away 9 apples (9x). You are left with -1 apple, or simply -1x or -x. This simple analogy helps illustrate the concept of combining like terms and dealing with negative values.
Expanding the Concept: Simplifying More Complex Expressions
The principles we used to simplify 8x - 9x are applicable to more complex algebraic expressions. Let's consider a few examples:
Example 1: 5y + 2y - 3y
Here, all terms are like terms (they all contain the variable 'y'). We add and subtract the coefficients: 5 + 2 - 3 = 4. Therefore, 5y + 2y - 3y = 4y.
Example 2: 3a² + 7a - 2a² + 4a
In this example, we have both a² and a terms. We combine like terms separately:
- a² terms: 3a² - 2a² = 1a² or simply a²
- a terms: 7a + 4a = 11a
Combining the simplified terms, we get a² + 11a.
Example 3: 2x²y + 5xy² - x²y + 3xy²
Here, we have terms with different combinations of variables. We can only combine terms that are exactly alike:
- x²y terms: 2x²y - x²y = x²y
- xy² terms: 5xy² + 3xy² = 8xy²
Combining the simplified terms, we have x²y + 8xy².
These examples demonstrate that the process of simplifying involves identifying like terms and performing the arithmetic operations on their coefficients. Remember, you cannot combine unlike terms (terms with different variables or different powers of the same variable).
The Importance of Order of Operations (PEMDAS/BODMAS)
When dealing with more complex expressions involving multiple operations (addition, subtraction, multiplication, division, exponents, parentheses/brackets), it is crucial to follow the order of operations, often remembered by the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction). This ensures that you simplify the expression correctly.
For example, consider the expression: 3x + 2(4x - 5)
Following PEMDAS/BODMAS, we first address the parentheses:
2(4x - 5) = 8x - 10
Now, we substitute this back into the original expression:
3x + 8x - 10
Then, we combine like terms:
3x + 8x = 11x
The simplified expression is 11x - 10.
Applications of Simplifying Algebraic Expressions
Simplifying algebraic expressions isn't just an abstract mathematical exercise. It's a fundamental skill with broad applications in various fields, including:
-
Solving equations: Simplifying expressions helps to make equations more manageable and easier to solve.
-
Graphing functions: Simplified expressions are essential for understanding and graphing functions accurately.
-
Calculus: Simplifying expressions is a prerequisite for many calculus operations like differentiation and integration.
-
Physics and Engineering: Many physical laws and engineering formulas are expressed using algebraic expressions that need to be simplified for practical applications.
-
Computer programming: Simplifying expressions improves the efficiency and readability of computer code.
Frequently Asked Questions (FAQ)
Q: What happens if I have more than two like terms?
A: You simply extend the same process. Add or subtract the coefficients of all like terms to find the simplified coefficient for that term. For example, 2x + 5x - x + 3x = (2 + 5 - 1 + 3)x = 9x.
Q: Can I simplify terms with different variables?
A: No, you cannot combine unlike terms. For example, 3x + 2y cannot be simplified further because x and y are different variables.
Q: What if the coefficient is 1 or -1?
A: If the coefficient is 1, it's usually omitted (e.g., 1x is written as x). If the coefficient is -1, you typically write -x instead of -1x.
Q: What if I have a more complex expression with multiple variables and exponents?
A: Follow the same principle: identify like terms (terms with the exact same variables raised to the same powers) and combine their coefficients. Remember to follow the order of operations (PEMDAS/BODMAS).
Q: Are there online tools to help simplify algebraic expressions?
A: Yes, many online calculators and software programs can help simplify algebraic expressions. However, understanding the underlying principles is crucial for effectively using these tools and for solving problems where such tools might not be available.
Conclusion
Simplifying algebraic expressions, even a seemingly basic one like 8x - 9x, is a cornerstone of algebraic manipulation. Mastering this skill involves a clear understanding of like terms, coefficients, variables, and the order of operations. The ability to simplify expressions efficiently and accurately is vital not only for succeeding in mathematics but also for applying mathematical principles in various scientific, engineering, and computational contexts. This article has provided a comprehensive guide, encompassing the fundamental principles, illustrative examples, and frequently asked questions, equipping you with the tools and knowledge to confidently tackle a wide range of algebraic simplification problems. Remember, practice is key to mastering this skill. So, keep practicing, and you'll find simplifying algebraic expressions becomes increasingly intuitive and effortless.
Latest Posts
Latest Posts
-
Is 4 10 Equivalent To 2 5
Sep 20, 2025
-
12 16 Reduced To Lowest Terms
Sep 20, 2025
-
500 Square Meter In Feet
Sep 20, 2025
-
8 40 As A Percent
Sep 20, 2025
-
4 Way Venn Diagram Generator
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Simplify 8x - 9x Completely . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.