10 X 1 1 2
saludintensiva
Sep 23, 2025 · 6 min read
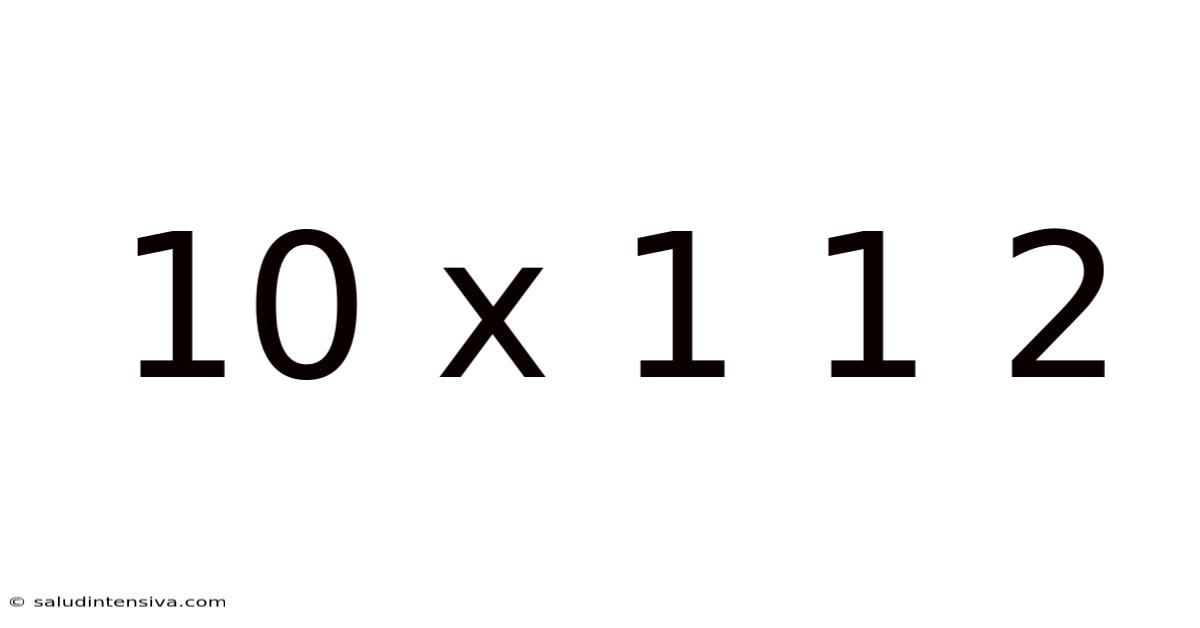
Table of Contents
Decoding 10 x 1 1 2: Exploring the Mysteries of a Seemingly Simple Equation
The seemingly simple expression "10 x 1 1 2" initially presents a puzzle. It lacks the clarity of a standard mathematical equation, leaving room for interpretation and multiple potential solutions. This ambiguity, however, opens the door to exploring fundamental mathematical concepts, order of operations, and the importance of precise notation. This article will delve into the possible interpretations of this expression, providing a detailed explanation of each approach and emphasizing the significance of clear mathematical communication. We will explore the role of implied multiplication, the order of operations (PEMDAS/BODMAS), and how differing interpretations can lead to vastly different results.
Understanding the Problem: Ambiguity and Interpretation
The core challenge with "10 x 1 1 2" lies in the absence of explicit operators between the numbers. Standard mathematical notation uses symbols like +, -, ×, and ÷ to clearly indicate the operation to be performed. The lack of these symbols introduces ambiguity. This means we must consider multiple potential interpretations before reaching a definitive answer. This is a crucial lesson in mathematics: precise notation is paramount to avoid confusion and ensure accurate results.
Potential Interpretations and Solutions
Let's examine the most plausible interpretations of "10 x 1 1 2":
Interpretation 1: Implied Multiplication and Concatenation
One possible interpretation treats the sequence "112" as a single number. This approach assumes implied multiplication between 10 and 112. Therefore:
10 x 112 = 1120
This interpretation assumes the spaces are simply separators and not indicative of any specific operation. While simple, it relies on an assumption that isn't explicitly stated.
Interpretation 2: Sequential Multiplication
Another interpretation involves treating each element as a separate factor in a sequential multiplication. This assumes multiplication between each number. The expression becomes:
10 × 1 × 1 × 2 = 20
This interpretation is equally valid as the first, highlighting how a simple change in assumed operations dramatically alters the outcome.
Interpretation 3: Introducing Addition or Subtraction (Highly Unlikely)
It's highly improbable, but conceivable, to introduce addition or subtraction into the equation. Without explicit operators, however, this approach is highly speculative. Examples of this would include:
- 10 + 1 + 1 + 2 = 14 (Adding all numbers together)
- 10 - 1 - 1 - 2 = 6 (Subtracting sequentially)
These interpretations are less likely given the presence of "x" suggesting a primarily multiplicative problem.
The Importance of Order of Operations (PEMDAS/BODMAS)
The order of operations, often remembered by the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction), plays a critical role in resolving mathematical expressions. While "10 x 1 1 2" doesn't explicitly contain parentheses or exponents, the order of multiplication and any potentially implied addition or subtraction becomes crucial if we choose to interpret it that way.
Let's reiterate the previous interpretations considering order of operations where applicable:
- Interpretation 1 (Implied Multiplication): This interpretation inherently adheres to the order of operations by performing the single multiplication first.
- Interpretation 2 (Sequential Multiplication): This interpretation again follows the order of operations, performing all multiplications from left to right.
- Interpretation 3 (Addition/Subtraction): If we were to introduce addition or subtraction, the order of operations would determine which operations are performed first.
Mathematical Notation and Clarity: A Crucial Lesson
The ambiguity of "10 x 1 1 2" underscores the crucial importance of precise mathematical notation. Clear and unambiguous notation prevents misinterpretations and ensures everyone arrives at the same correct solution. Using parentheses or explicitly stating the operations to be performed (e.g., 10 x (1 + 1 + 2) or 10 x 1 x 1 x 2) eliminates any potential confusion.
This example highlights how seemingly simple expressions can lead to vastly different results if the underlying assumptions and interpretations are not clearly defined. In real-world applications, especially in fields like engineering, programming, and finance, precise mathematical notation is essential to prevent costly errors.
Expanding on the Concepts: Exploring Related Mathematical Ideas
The analysis of "10 x 1 1 2" opens doors to explore related mathematical concepts:
- Implied Multiplication: Many mathematical expressions use implied multiplication, particularly in algebraic contexts. Understanding when and how implied multiplication is used is critical for accurate interpretation.
- Factorization: The expression can be viewed in terms of factorization, identifying the prime factors of the result. For example, if we adopt interpretation 2 (10 x 1 x 1 x 2 = 20), the prime factorization of 20 is 2² x 5.
- Number Systems: The expression could be explored within different number systems (binary, hexadecimal, etc.), further highlighting the importance of context and notation.
Practical Applications and Real-World Relevance
While the expression "10 x 1 1 2" might seem abstract, the principles involved are applicable in numerous real-world scenarios:
- Programming: In programming, the order of operations and explicit notation are crucial for writing clear and error-free code. Ambiguity can lead to unexpected program behavior or crashes.
- Financial Calculations: Accurate calculations are essential in finance. Misinterpretations of mathematical expressions could result in significant financial errors.
- Engineering and Physics: Precise mathematical calculations are fundamental to engineering and physics. Ambiguous notation can lead to design flaws or incorrect predictions.
Frequently Asked Questions (FAQ)
Q1: What is the "correct" answer to 10 x 1 1 2?
A1: There's no single "correct" answer without further clarification of the intended operations. The different interpretations presented above (1120 and 20) are both valid depending on how the expression is understood.
Q2: Why is this expression ambiguous?
A2: The ambiguity arises from the lack of explicit mathematical operators (like +, -, ×, ÷) between the numbers. This leaves room for multiple valid interpretations.
Q3: How can I avoid ambiguity in my own mathematical expressions?
A3: Always use clear and unambiguous notation. Use parentheses to group terms, explicitly state all operations, and maintain consistent spacing to enhance readability.
Q4: What is the importance of order of operations?
A4: The order of operations ensures that complex expressions are evaluated consistently, leading to a single, unambiguous result. Following the established order (PEMDAS/BODMAS) is essential for accurate calculations.
Q5: Can this expression be interpreted in other number systems?
A5: Yes, but the interpretation and outcome would depend heavily on the specific number system and how the numerals are defined within that system. This would introduce further complexities.
Conclusion: The Power of Precise Mathematical Communication
The seemingly simple expression "10 x 1 1 2" serves as a powerful reminder of the importance of clear and unambiguous mathematical notation. The multiple interpretations and resulting answers highlight the necessity of precise communication to avoid confusion and ensure accurate results. This lesson transcends the simple equation itself, emphasizing the fundamental importance of clear communication in all areas of mathematics and its applications in the real world. Understanding implied multiplication, the order of operations, and the impact of notation are crucial skills for anyone working with mathematics, regardless of their level of expertise. The ambiguity of this equation serves as a valuable teaching tool, highlighting the need for precision and clarity in all mathematical work.
Latest Posts
Latest Posts
-
How Thick Concrete For Sidewalk
Sep 23, 2025
-
10 Divided By 5 6
Sep 23, 2025
-
90 Days From August 26
Sep 23, 2025
-
Energy Stored Due To Elevation
Sep 23, 2025
-
What Is 55c In F
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 10 X 1 1 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.