10 X 20 X 4
saludintensiva
Sep 21, 2025 · 6 min read
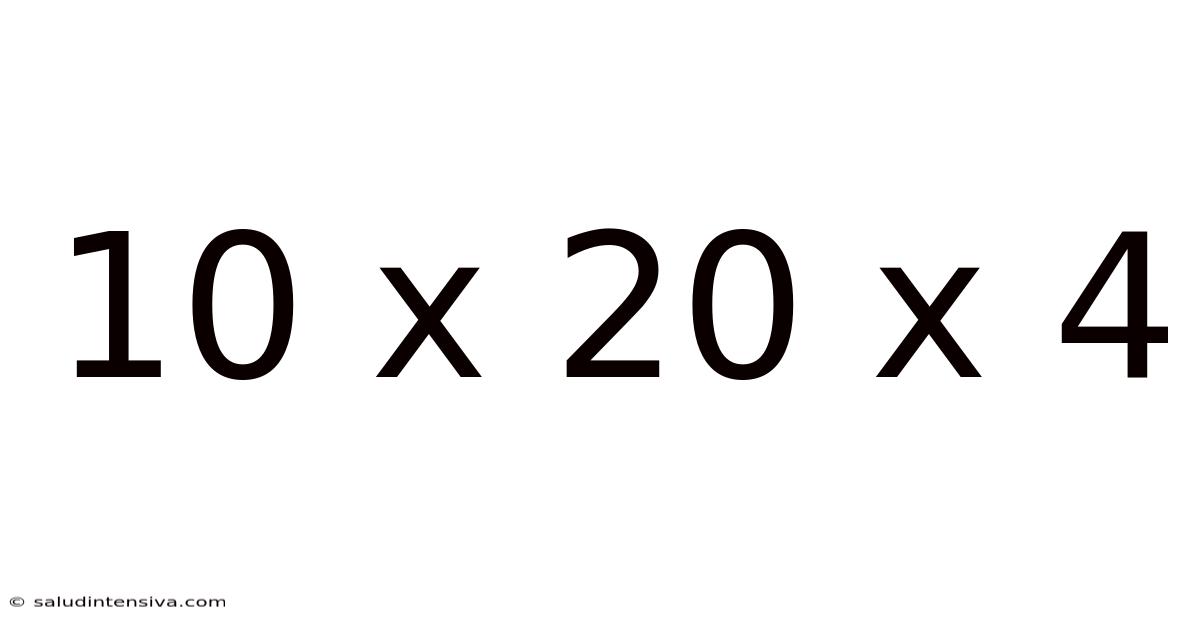
Table of Contents
Decoding 10 x 20 x 4: Exploring Dimensions, Volume, and Applications
This seemingly simple expression, "10 x 20 x 4," represents much more than just a series of numbers. It fundamentally describes dimensions – length, width, and height – which in turn define volume and ultimately dictate the potential applications of a three-dimensional space. Understanding this seemingly simple concept unlocks a deeper appreciation for geometry, spatial reasoning, and practical applications across various fields. This article will delve into the meaning of these dimensions, explore the calculation of volume, and investigate the diverse contexts in which such dimensions are utilized.
Understanding the Dimensions: Length, Width, and Height
The expression "10 x 20 x 4" defines a rectangular prism (or cuboid) using three key dimensions:
- 10: This represents the length of the rectangular prism. It is the longest continuous measurement of one side.
- 20: This represents the width of the rectangular prism. It's the measurement of the side perpendicular to the length.
- 4: This represents the height of the rectangular prism. It's the measurement of the side extending upwards from the base.
These dimensions are typically measured in the same unit. For example, it could be 10 meters x 20 meters x 4 meters, 10 centimeters x 20 centimeters x 4 centimeters, or 10 inches x 20 inches x 4 inches. The choice of unit depends entirely on the context and scale of the object being described. Failing to specify the unit makes the dimensions abstract and less useful for practical applications.
Calculating the Volume
The primary application of understanding these dimensions is in calculating the volume of the rectangular prism. The volume represents the amount of three-dimensional space enclosed within the prism's boundaries. It is calculated by multiplying the three dimensions together:
Volume = Length x Width x Height
In this case:
Volume = 10 x 20 x 4 = 800
Again, the unit of volume depends on the unit used for the dimensions. If the dimensions are in meters, the volume is 800 cubic meters (m³). If the dimensions are in centimeters, the volume is 800 cubic centimeters (cm³), and so on.
Practical Applications Across Diverse Fields
The dimensions 10 x 20 x 4, and the resultant volume of 800 cubic units, find applications in a surprisingly broad range of fields. Let's explore some examples:
-
Construction and Engineering: These dimensions might represent the size of a room, a section of a building, or even a component in a larger structure. Understanding the volume is crucial for calculating the amount of materials needed, such as concrete, bricks, or insulation. A contractor might use these dimensions to plan the space and order the necessary materials.
-
Manufacturing and Packaging: Many products are packaged in boxes with these or similar dimensions. Manufacturers need to optimize packaging size to minimize waste and shipping costs while ensuring the product is protected. Knowing the volume helps in determining the number of items that can be shipped in a container of a specific size.
-
Agriculture and Horticulture: These dimensions could describe the size of a greenhouse, a hydroponic growing system, or a storage unit for agricultural products. The volume is important for determining the growing space available and the capacity for storing harvested crops.
-
Logistics and Shipping: Containers used for shipping goods often have dimensions that are multiples or fractions of these dimensions. Understanding the volume allows for efficient packing and utilization of shipping space. The volume calculation directly affects shipping costs.
-
Aquariums and Fish Tanks: Aquariums and fish tanks often have similar proportions. The volume of the tank is crucial for determining the number of fish and the type of filtration system required. A larger volume allows for more fish and reduces the stress on the environment.
-
Data Storage and Computing: While not directly related to physical dimensions, the concept of "10 x 20 x 4" can be applied metaphorically to represent data structures. Imagine a 3D array with these dimensions. The volume would represent the total number of data points or elements within this structure.
-
Residential Design: A home might have rooms with dimensions similar to this, and the understanding of volume is crucial for everything from heating and cooling calculations to furnishing plans.
Beyond the Numbers: Considerations for Practical Application
While the calculation of volume is straightforward, several factors should be considered when applying these dimensions in real-world scenarios:
-
Unit of Measurement: Always specify the unit of measurement (meters, centimeters, feet, inches, etc.) to avoid ambiguity.
-
Material Properties: The material used to construct an object with these dimensions will influence its weight and structural integrity. This needs to be factored into design and construction plans.
-
Tolerances: In manufacturing and engineering, tolerances account for slight variations in dimensions. It's rare to achieve perfectly precise measurements.
-
Scale: The scale of the application significantly impacts the relevance of these dimensions. 10 x 20 x 4 meters is vastly different from 10 x 20 x 4 millimeters.
FAQ
-
Q: What is the surface area of a rectangular prism with dimensions 10 x 20 x 4?
- A: The surface area is calculated as 2(lw + lh + wh), where l is length, w is width, and h is height. In this case, the surface area is 2(1020 + 104 + 20*4) = 680 square units. The unit will be square meters if the dimensions were in meters, and so on.
-
Q: Can these dimensions be used to describe any shape other than a rectangular prism?
- A: No, these three dimensions specifically define a rectangular prism. Other shapes require different sets of dimensions or parameters.
-
Q: What if one of the dimensions is zero?
- A: If any dimension is zero, the resulting volume is zero. This implies a two-dimensional object or a line.
-
Q: How are these dimensions used in 3D modeling software?
- A: These dimensions are fundamental input parameters in 3D modeling software. They define the basic size and shape of an object which can then be further modified and manipulated.
Conclusion
The seemingly simple expression "10 x 20 x 4" provides a foundation for understanding three-dimensional space, volume calculations, and their wide-ranging applications. From engineering and manufacturing to agriculture and shipping, the ability to interpret and utilize these dimensions is crucial across numerous disciplines. By grasping the fundamental concepts of length, width, height, and volume, one can better comprehend and engage with the three-dimensional world around us. The seemingly simple act of multiplying these numbers reveals a world of practical applications and possibilities. Understanding this core concept empowers individuals to solve problems, make informed decisions, and contribute effectively to various fields.
Latest Posts
Latest Posts
-
90 Days From June 13
Sep 22, 2025
-
34 9 As A Mixed Number
Sep 22, 2025
-
2 8 Repeating As A Fraction
Sep 22, 2025
-
Images Of A Square Prism
Sep 22, 2025
-
Ratio Word Problems 7th Grade
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about 10 X 20 X 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.