11/7 As A Mixed Number
saludintensiva
Sep 23, 2025 · 6 min read
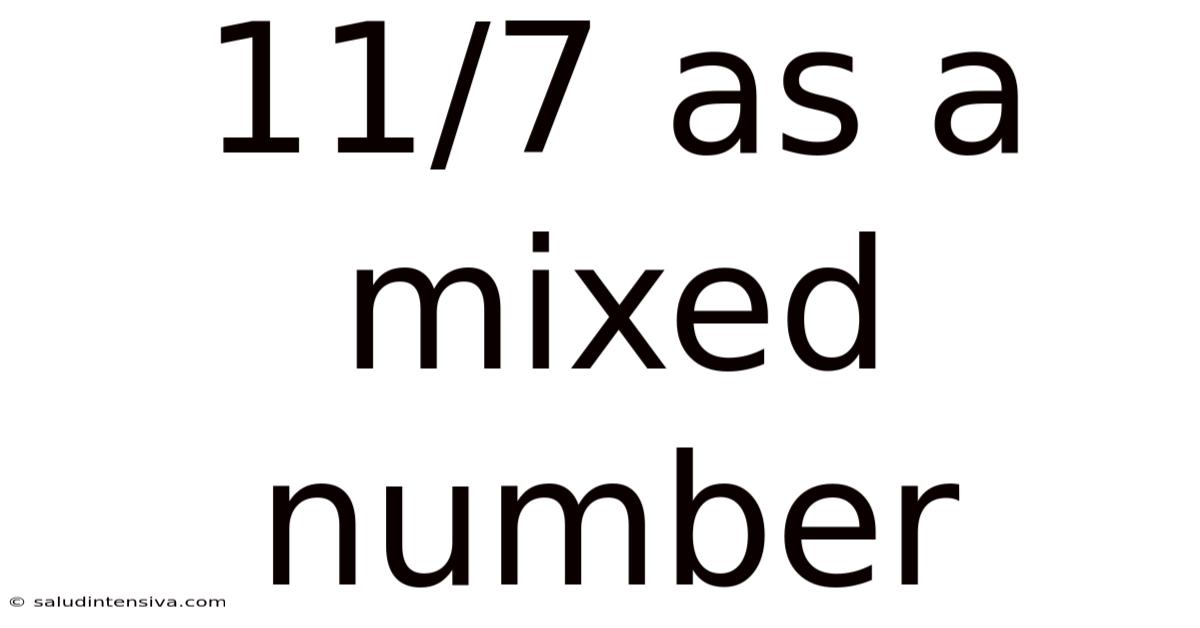
Table of Contents
Understanding 11/7 as a Mixed Number: A Comprehensive Guide
The fraction 11/7 represents a value greater than one. Understanding how to convert improper fractions like 11/7 into mixed numbers is a fundamental skill in mathematics, crucial for various applications from baking to engineering. This comprehensive guide will walk you through the process of converting 11/7 to a mixed number, explore the underlying concepts, and delve into practical examples. We'll also address common questions and misconceptions surrounding this mathematical operation.
What is a Mixed Number?
Before we tackle the conversion of 11/7, let's clarify what a mixed number is. A mixed number combines a whole number and a proper fraction. A proper fraction is a fraction where the numerator (the top number) is smaller than the denominator (the bottom number). For instance, 1 ½, 3 ¼, and 5 ⅔ are all examples of mixed numbers. They represent values greater than one, expressing the quantity as a whole number and a remaining fractional part.
Converting 11/7 to a Mixed Number: Step-by-Step
The conversion of an improper fraction (where the numerator is larger than the denominator) to a mixed number involves a simple division process. Let's break it down step-by-step for 11/7:
Step 1: Perform the Division
Divide the numerator (11) by the denominator (7).
11 ÷ 7 = 1 with a remainder of 4
Step 2: Identify the Whole Number
The quotient (the result of the division) becomes the whole number part of your mixed number. In this case, the quotient is 1.
Step 3: Identify the Fraction
The remainder (4) becomes the numerator of the fractional part of your mixed number. The denominator remains the same as the original fraction (7).
Step 4: Write the Mixed Number
Combine the whole number and the fraction to form the mixed number. Therefore, 11/7 as a mixed number is 1 ⁴⁄₇.
Visualizing the Conversion
Imagine you have 11 pizzas, and you want to share them equally among 7 friends. You can give each friend one whole pizza (that's the '1' in our mixed number). You'll have 4 pizzas left over (the remainder), which you can divide among your 7 friends, resulting in each friend getting an additional ⁴⁄₇ of a pizza. This visual representation perfectly illustrates the concept behind converting an improper fraction to a mixed number.
Understanding the Underlying Mathematical Principles
The conversion from an improper fraction to a mixed number is based on the fundamental principle of equivalent fractions. The improper fraction 11/7 represents the same quantity as the mixed number 1 ⁴⁄₇. We can demonstrate this equivalence:
1 ⁴⁄₇ = (1 x 7)/7 + ⁴⁄₇ = ⁷⁄₇ + ⁴⁄₇ = ¹¹⁄₇
This equation shows that we can express the whole number '1' as ⁷⁄₇ (a fraction with the same denominator as the remainder). Adding this equivalent fraction to the remainder fraction (⁴⁄₇) gives us the original improper fraction ¹¹⁄₇. This equivalence holds true for all improper fraction to mixed number conversions.
Practical Applications of Mixed Numbers
Mixed numbers are incredibly useful in various real-world scenarios. Here are a few examples:
-
Cooking and Baking: Recipes often call for measurements like 2 ½ cups of flour or 1 ¾ teaspoons of baking powder. Mixed numbers are the standard way to represent these quantities.
-
Measurement and Construction: Measuring lengths, heights, and widths frequently involves mixed numbers, particularly in fields like carpentry and engineering.
-
Time: We use mixed numbers to represent durations, such as 1 hour and 15 minutes (which can be represented as 1 ¼ hours).
-
Data Analysis and Statistics: Mixed numbers can appear in statistical data representing averages or proportions.
-
Everyday Calculations: Many everyday problems that involve fractions will benefit from representing the results as mixed numbers for clearer understanding and easier interpretation.
Converting Mixed Numbers Back to Improper Fractions
It's important to understand that the conversion between improper fractions and mixed numbers is reversible. To convert a mixed number back to an improper fraction, follow these steps:
Step 1: Multiply the whole number by the denominator.
In our example (1 ⁴⁄₇), multiply 1 by 7, which equals 7.
Step 2: Add the numerator.
Add the result from step 1 (7) to the numerator of the fraction (4), resulting in 11.
Step 3: Write the improper fraction.
This sum (11) becomes the numerator of the improper fraction, while the denominator remains the same (7). Thus, 1 ⁴⁄₇ converts back to ¹¹⁄₇.
Frequently Asked Questions (FAQ)
Q1: What if the remainder is zero after dividing the numerator by the denominator?
A1: If the remainder is zero, it means the improper fraction is actually a whole number. For example, 14/7 = 2. There's no fractional part in this case.
Q2: Can I convert any improper fraction into a mixed number?
A2: Yes, any improper fraction can be converted into a mixed number or a whole number. This is because an improper fraction inherently represents a value greater than or equal to one.
Q3: Why is it important to understand improper fractions and mixed numbers?
A3: Understanding both forms is crucial for a strong foundation in mathematics. It allows for flexible problem-solving and clear communication of fractional quantities. Many real-world applications rely on the ability to switch between these two representations.
Q4: Are there different ways to represent the same value using fractions?
A4: Yes, absolutely. A single value can be expressed as an improper fraction, a mixed number, or even a decimal. The choice of representation often depends on the context and the preferred level of precision.
Q5: How do I choose between using an improper fraction or a mixed number in a problem?
A5: The choice often depends on the specific problem and context. Improper fractions are generally preferred for calculations, as they are easier to manipulate algebraically. Mixed numbers are more intuitive and easier to visualize in many real-world situations.
Conclusion
Converting an improper fraction like 11/7 to a mixed number is a fundamental mathematical skill with broad applications. This guide has comprehensively explored the process, underlying principles, and practical uses of mixed numbers. By understanding these concepts and mastering the conversion techniques, you'll gain a stronger foundation in mathematics and enhance your ability to solve problems involving fractions in various contexts. Remember that the key to success lies in practice. Work through various examples, and you'll soon find this operation second nature. The more you practice, the more confident and proficient you will become in handling fractions and mixed numbers. This will not only improve your mathematical skills but also boost your problem-solving abilities across a wide range of applications.
Latest Posts
Latest Posts
-
1 Yard Of Mulch Weight
Sep 23, 2025
-
How Thick Concrete For Sidewalk
Sep 23, 2025
-
10 Divided By 5 6
Sep 23, 2025
-
90 Days From August 26
Sep 23, 2025
-
Energy Stored Due To Elevation
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 11/7 As A Mixed Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.