11 9 As A Decimal
saludintensiva
Sep 13, 2025 · 6 min read
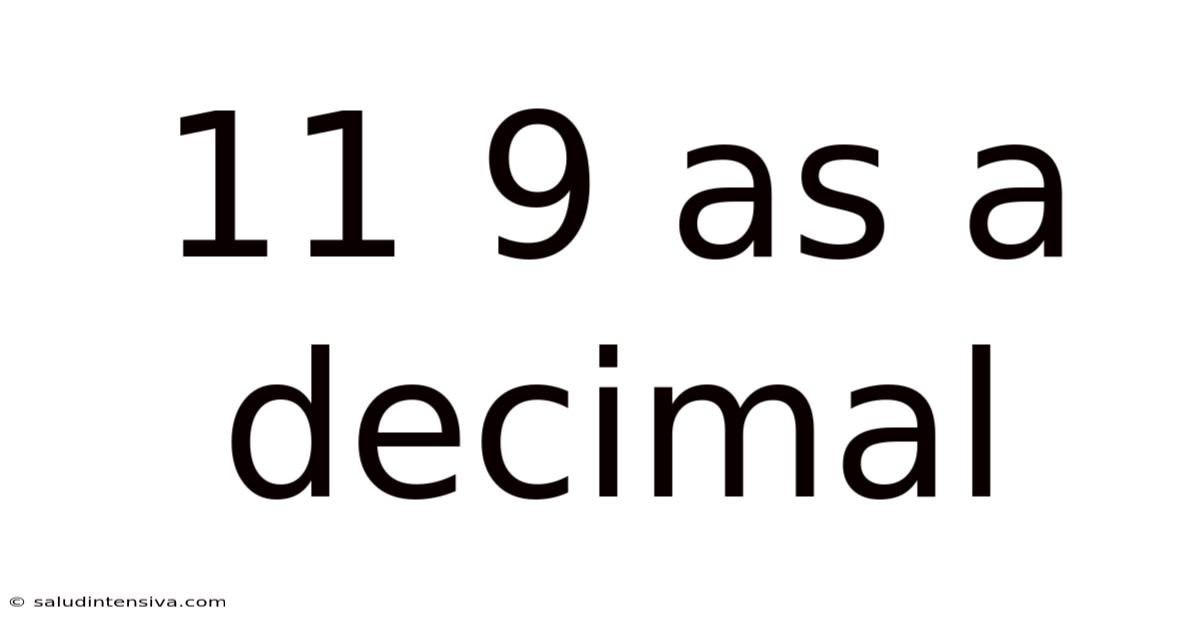
Table of Contents
11/9 as a Decimal: A Comprehensive Guide to Fraction-to-Decimal Conversion
Understanding how to convert fractions to decimals is a fundamental skill in mathematics. This comprehensive guide will delve deep into converting the fraction 11/9 into its decimal equivalent, exploring various methods and providing a solid understanding of the underlying principles. We'll cover not only the calculation itself but also the broader context of rational numbers and their decimal representations. By the end, you'll be equipped to confidently tackle similar fraction-to-decimal conversions and have a deeper grasp of number systems.
Introduction: Fractions and Decimals – A Unified System
Before diving into the specifics of 11/9, let's establish a foundational understanding. Both fractions and decimals represent parts of a whole. A fraction expresses a part as a ratio of two integers – the numerator (top number) and the denominator (bottom number). A decimal represents a part using the base-10 number system, where digits to the right of the decimal point represent tenths, hundredths, thousandths, and so on. Essentially, fractions and decimals are two different ways of expressing the same numerical value.
The fraction 11/9, in particular, represents eleven ninths. This means we have eleven parts out of a total of nine parts. Since the numerator is larger than the denominator, this is an improper fraction, indicating a value greater than one. Converting this to a decimal will reveal this characteristic clearly.
Method 1: Long Division
The most straightforward method for converting a fraction to a decimal is through long division. To convert 11/9 to a decimal, we divide the numerator (11) by the denominator (9):
1.222...
9 | 11.000
-9
---
20
-18
---
20
-18
---
20
-18
---
2...
As you can see, the division results in a repeating decimal: 1.222... The digit '2' repeats infinitely. This is denoted mathematically as 1.2̅. The bar above the '2' indicates the repeating part of the decimal.
Method 2: Understanding the Concept of Repeating Decimals
The repeating nature of the decimal representation of 11/9 is not coincidental. It arises because the fraction cannot be simplified to have a denominator that is a power of 10 (10, 100, 1000, etc.). Fractions with denominators that can be expressed as powers of 10 will always convert to terminating decimals (decimals that end). For example, 1/2 = 0.5, 1/4 = 0.25, and 1/10 = 0.1. However, 11/9, even after simplification, still has a denominator of 9, which is not a power of 10.
This leads to the concept of rational numbers. Rational numbers are numbers that can be expressed as a fraction of two integers. All rational numbers have either terminating or repeating decimal representations. Irrational numbers, on the other hand, like π (pi) or √2 (the square root of 2), have non-terminating and non-repeating decimal representations.
Method 3: Converting to a Mixed Number (Optional)
Before performing the long division, we could convert the improper fraction 11/9 into a mixed number. A mixed number combines a whole number and a fraction. To do this, we divide the numerator (11) by the denominator (9):
11 ÷ 9 = 1 with a remainder of 2
This means 11/9 can be written as 1 and 2/9.
Now, we only need to convert the fractional part, 2/9, to a decimal using long division:
0.222...
9 | 2.000
-1.8
---
0.20
-0.18
---
0.020
-0.018
---
0.002...
This gives us 0.2̅. Adding the whole number part (1) back, we get 1.2̅, confirming the result from the previous method.
Understanding the Repeating Pattern: A Deeper Dive
The repeating decimal 1.2̅ is a fascinating example of mathematical patterns. The repetition arises from the cyclical nature of the long division process. When we continue the long division, the remainder keeps cycling through the same values (in this case, 2). This cyclic pattern of remainders directly corresponds to the repeating digits in the decimal representation.
This concept highlights the inherent relationship between fractions and their decimal expansions. Every repeating decimal can be expressed as a fraction, and every fraction with a denominator that is not a power of 10 or doesn't cancel down to a power of 10 will produce a repeating or recurring decimal.
Practical Applications: Why This Matters
The ability to convert fractions to decimals is crucial in various fields:
- Science and Engineering: Many scientific and engineering calculations involve both fractions and decimals. Converting between the two is often necessary for accurate computations.
- Finance: Working with money involves fractions (e.g., expressing parts of a dollar) and decimals (e.g., representing monetary values).
- Everyday Life: Many situations require understanding fractional and decimal representations, such as measuring ingredients in cooking or calculating discounts in shopping.
Beyond 11/9: Generalizing the Process
The methods explained here can be applied to convert any fraction to a decimal. Remember, if the denominator is a power of 10, the decimal will terminate. Otherwise, you'll likely encounter a repeating decimal. The key is to understand the process of long division and the relationship between the remainders and the repeating digits.
Frequently Asked Questions (FAQ)
-
Q: What is the difference between a terminating and a repeating decimal?
- A: A terminating decimal has a finite number of digits after the decimal point (e.g., 0.5, 0.75). A repeating decimal has an infinite number of digits that repeat in a pattern (e.g., 0.333..., 0.142857142857...).
-
Q: How can I express 1.2̅ as a fraction?
- A: Let x = 1.2̅. Then 10x = 12.2̅. Subtracting x from 10x, we get 9x = 11, so x = 11/9. This demonstrates the inverse operation of converting a repeating decimal back to a fraction.
-
Q: Are there other ways to convert fractions to decimals besides long division?
- A: While long division is the most fundamental method, calculators can directly perform the conversion. Moreover, some fractions can be mentally converted by recognizing equivalent fractions with denominators that are powers of 10 (e.g., 1/2 = 5/10 = 0.5).
-
Q: What if the fraction has a large denominator?
- A: Long division may be more time-consuming with large denominators. Using a calculator is recommended in such cases, although understanding the underlying principle remains essential.
Conclusion: Mastering Fraction-to-Decimal Conversion
Converting 11/9 to its decimal equivalent (1.2̅) highlights the crucial connection between fractions and decimals within the broader context of number systems. By understanding the methods of long division and the concept of repeating decimals, you've gained a valuable mathematical skill applicable across diverse fields. Remember, this skill is not just about calculation; it's about understanding the underlying mathematical principles and their real-world significance. Practice converting different fractions to decimals, and you’ll quickly build confidence and proficiency. The more you explore these concepts, the deeper your understanding of the elegance and interconnectedness of mathematics will become.
Latest Posts
Latest Posts
-
2 5 Million Seconds To Days
Sep 13, 2025
-
Double Declining Balance Depreciation Method
Sep 13, 2025
-
What Is Half Of 28
Sep 13, 2025
-
6 Repeating As A Fraction
Sep 13, 2025
-
What Is 0 6 In Fraction
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about 11 9 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.