12 13 As A Percentage
saludintensiva
Sep 12, 2025 · 5 min read
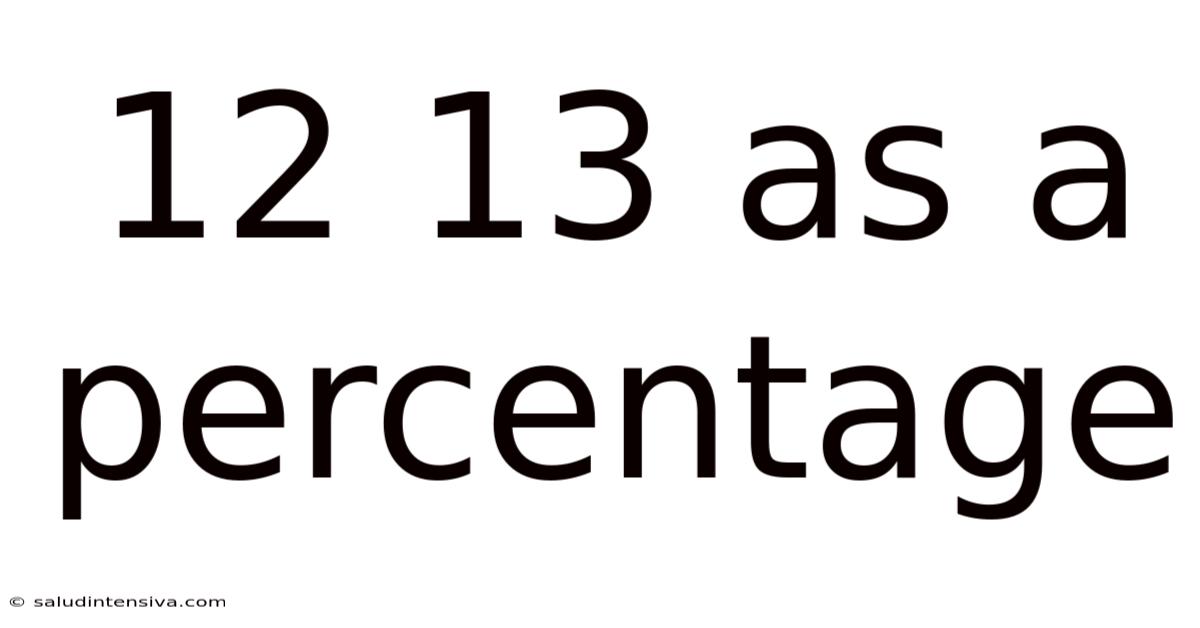
Table of Contents
Understanding 12/13 as a Percentage: A Comprehensive Guide
What percentage is 12 out of 13? This seemingly simple question underlies a fundamental concept in mathematics: expressing parts of a whole as percentages. Understanding how to calculate percentages is crucial in various aspects of life, from calculating grades and discounts to analyzing financial data and understanding statistical information. This article will provide a comprehensive explanation of how to determine 12/13 as a percentage, delve into the underlying mathematical principles, and explore practical applications. We'll also address common questions and misconceptions surrounding percentage calculations.
Understanding Percentages
A percentage is simply a fraction where the denominator is 100. It represents a part of a whole, expressed as a proportion of 100. The symbol "%" represents "per cent," meaning "out of one hundred." For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Calculating 12/13 as a Percentage: Step-by-Step
To find what percentage 12 is of 13, we need to convert the fraction 12/13 into a percentage. Here's the step-by-step process:
Step 1: Divide the numerator by the denominator.
This involves dividing 12 by 13:
12 ÷ 13 ≈ 0.923
Step 2: Multiply the result by 100.
This converts the decimal into a percentage:
0.923 x 100 = 92.3%
Therefore, 12 out of 13 is approximately 92.3%.
Alternative Methods for Percentage Calculation
While the method above is straightforward, there are alternative approaches, especially useful for those who prefer different calculation styles or who are working with more complex scenarios.
Method 1: Using Proportions
We can set up a proportion:
12/13 = x/100
To solve for x (the percentage), we cross-multiply:
13x = 1200
x = 1200/13 ≈ 92.3%
This method emphasizes the relationship between fractions and percentages, clearly showing how the proportion is maintained.
Method 2: Using a Calculator
Most calculators have a percentage function. Simply enter 12 ÷ 13 and then multiply by 100 to get the percentage directly. This method is efficient and minimizes the risk of manual calculation errors.
Understanding the Result: 92.3%
The result, 92.3%, indicates that 12 represents approximately 92.3% of 13. This signifies that if we divide 13 into 100 equal parts, 12 would occupy 92.3 of those parts. This understanding is crucial for interpreting data and making informed decisions in various contexts.
Practical Applications of Percentage Calculations
The ability to calculate percentages is a valuable skill applicable across numerous fields:
-
Academic Performance: Calculating grades based on marks obtained in tests and assignments. For example, if a student scores 12 out of 13 on a quiz, their percentage score is 92.3%.
-
Finance: Calculating interest rates, discounts, taxes, and profit margins. Understanding percentages is essential for making sound financial decisions, comparing investment options, and managing personal finances effectively.
-
Statistics: Analyzing data and presenting findings in a clear and concise way. Percentages are crucial for interpreting statistical data, identifying trends, and communicating research findings effectively.
-
Business and Economics: Calculating market share, growth rates, and inflation rates. Percentages are essential tools for business analysts, economists, and market researchers to understand and predict economic trends.
-
Everyday Life: Determining discounts in stores, calculating tips in restaurants, and understanding proportions in cooking recipes. Percentage calculations are frequently used in everyday situations, making it a valuable life skill.
Addressing Common Misconceptions
Several misconceptions surround percentage calculations:
-
Incorrectly adding percentages: Adding percentages directly is often incorrect. For instance, a 10% increase followed by a 10% decrease does not result in the original value. This is because the second percentage is calculated on a new, adjusted value.
-
Confusion with decimals and fractions: Understanding the relationship between fractions, decimals, and percentages is key to avoiding errors. Properly converting between these forms is essential for accurate calculations.
-
Rounding errors: When rounding decimals, slight variations can occur. It's crucial to consider the level of precision required for the specific application. In some instances, it's acceptable to round to the nearest whole number, while in others, greater precision might be necessary.
Further Exploration: Working with Percentages
Once you've mastered the basics of calculating percentages, you can explore more complex scenarios:
-
Percentage increase and decrease: Calculating the percentage change between two values. For example, finding the percentage increase in sales from one year to the next.
-
Compound percentages: Calculating percentages that are applied sequentially, taking into account the effect of previous calculations (like compound interest).
-
Percentage points: Understanding the difference between percentage change and percentage points. Percentage points represent the absolute difference between two percentages.
Frequently Asked Questions (FAQs)
Q: What if I have a fraction that doesn't divide evenly?
A: In most cases, you'll obtain a decimal value. You can either leave the answer as a decimal percentage (like 92.3%) or round it to a whole number or a certain number of decimal places depending on the required precision.
Q: How do I calculate a percentage of a number?
A: To find a percentage of a number, convert the percentage to a decimal (by dividing by 100) and then multiply the decimal by the number. For example, 25% of 80 is 0.25 x 80 = 20.
Q: What is the difference between a fraction and a percentage?
A: A fraction represents a part of a whole as a ratio of two numbers (numerator/denominator). A percentage is a specific type of fraction where the denominator is always 100.
Q: Can I use a spreadsheet program like Excel to calculate percentages?
A: Yes, spreadsheet programs like Excel have built-in functions for calculating percentages, making it easier to perform calculations, especially with larger datasets.
Conclusion
Calculating 12/13 as a percentage, resulting in approximately 92.3%, demonstrates a fundamental skill applicable across diverse fields. Mastering percentage calculations enhances one's ability to analyze data, make informed decisions, and understand various aspects of the world around us. By understanding the underlying principles and applying the methods outlined in this article, you can confidently tackle various percentage-related problems and leverage this essential mathematical skill in your personal and professional life. Remember, practice is key to mastering this valuable skill. Try working through different examples and gradually increase the complexity of the problems to solidify your understanding.
Latest Posts
Latest Posts
-
What Is 1 3 4 5
Sep 12, 2025
-
Calculate Square Footage Of Yard
Sep 12, 2025
-
Gcf Of 60 And 40
Sep 12, 2025
-
Convert 500 Kg To Pounds
Sep 12, 2025
-
2 Out Of 5 Percentage
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 12 13 As A Percentage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.