What Is 1/3 + 4/5
saludintensiva
Sep 12, 2025 · 5 min read
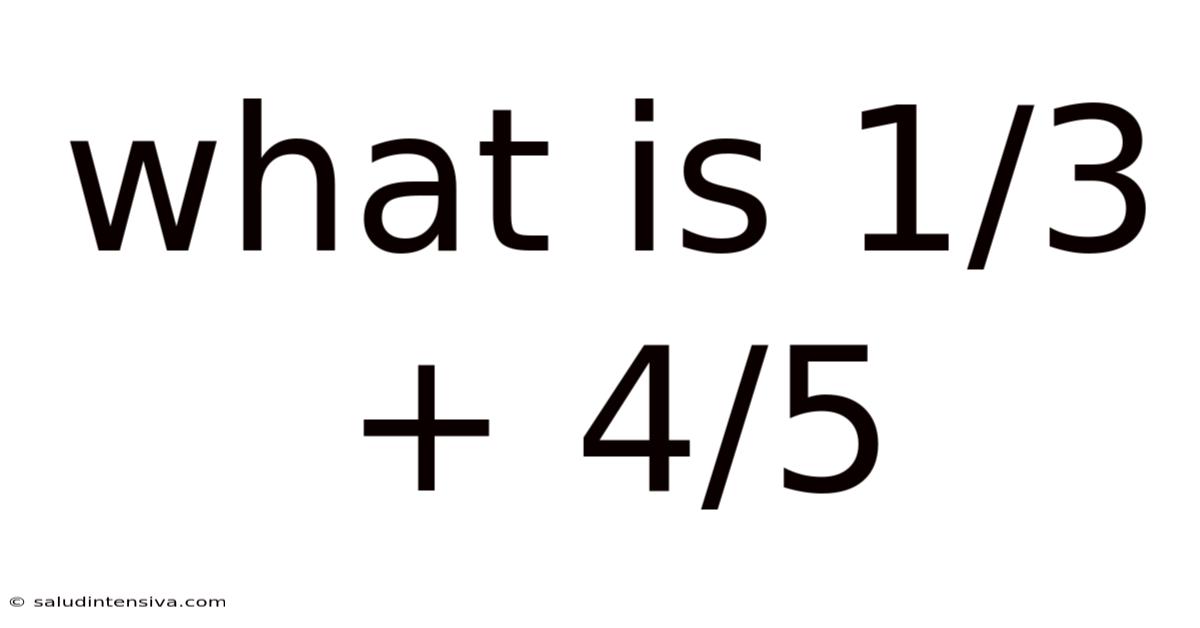
Table of Contents
What is 1/3 + 4/5? A Deep Dive into Fraction Addition
This article will guide you through the process of adding fractions, specifically addressing the common question: What is 1/3 + 4/5? We'll cover the fundamental concepts of fraction addition, explain the steps involved in solving this particular problem, and explore the underlying mathematical principles. This comprehensive guide is designed for anyone, from students just learning about fractions to those looking to refresh their mathematical skills. We'll also delve into some frequently asked questions and explore the broader context of fraction arithmetic.
Understanding Fractions: A Quick Refresher
Before tackling the addition of 1/3 and 4/5, let's refresh our understanding of fractions. A fraction represents a part of a whole. It consists of two key components:
- Numerator: The top number, indicating how many parts we have.
- Denominator: The bottom number, indicating how many equal parts the whole is divided into.
For example, in the fraction 1/3, the numerator (1) represents one part, and the denominator (3) indicates that the whole is divided into three equal parts.
Adding Fractions: The Core Principles
The crucial rule for adding fractions is that the denominators must be the same. Think of it like adding apples and oranges – you can't directly add them unless you have a common unit. If the denominators are different, we need to find a common denominator before we can add the fractions.
Step-by-Step Solution: 1/3 + 4/5
-
Find the Least Common Denominator (LCD): The LCD is the smallest number that is a multiple of both denominators (3 and 5). The multiples of 3 are 3, 6, 9, 12, 15, 18... The multiples of 5 are 5, 10, 15, 20... The smallest number that appears in both lists is 15. Therefore, our LCD is 15.
-
Convert the Fractions to Equivalent Fractions with the LCD: To change the denominator of 1/3 to 15, we multiply both the numerator and the denominator by 5:
(1/3) x (5/5) = 5/15
To change the denominator of 4/5 to 15, we multiply both the numerator and the denominator by 3:
(4/5) x (3/3) = 12/15
Notice that multiplying a fraction by a form of 1 (like 5/5 or 3/3) doesn't change its value; it just changes its representation.
-
Add the Numerators: Now that both fractions have the same denominator, we can add the numerators:
5/15 + 12/15 = (5 + 12)/15 = 17/15
-
Simplify the Result (if necessary): The resulting fraction, 17/15, is an improper fraction because the numerator (17) is larger than the denominator (15). We can convert this to a mixed number, which combines a whole number and a fraction. To do this, divide the numerator by the denominator:
17 ÷ 15 = 1 with a remainder of 2
Therefore, 17/15 is equivalent to 1 2/15.
Therefore, 1/3 + 4/5 = 17/15 = 1 2/15
A Deeper Look: The Mathematical Principles
The process of finding the LCD is essentially about finding the least common multiple (LCM) of the denominators. The LCM is the smallest number that is divisible by both numbers. For small numbers, this can be done by listing multiples. For larger numbers, prime factorization can be a more efficient method.
Prime factorization involves breaking down a number into its prime factors (numbers only divisible by 1 and themselves). For example, the prime factorization of 15 is 3 x 5. By finding the prime factorization of each denominator, we can identify the common factors and build the LCD.
Once we have equivalent fractions with the same denominator, the addition becomes straightforward: we simply add the numerators while keeping the denominator the same. This is because we are adding parts of the same whole.
Frequently Asked Questions (FAQs)
-
Why do we need a common denominator? Imagine you have 1/2 of a pizza and 1/4 of a pizza. You can't directly add them because the slices are different sizes. A common denominator ensures we are adding parts of the same size.
-
What if the fractions are negative? The process is the same, but remember the rules for adding negative numbers. For example, -1/3 + 4/5 would involve finding the LCD, converting to equivalent fractions, and then adding the numerators, paying attention to the signs.
-
Can I always simplify the result? Not always. Sometimes the resulting fraction is already in its simplest form. Simplifying means reducing the fraction to its lowest terms by dividing both the numerator and denominator by their greatest common divisor (GCD).
-
Are there other methods to add fractions? While the common denominator method is the most common and generally easiest, there are other approaches, particularly for more complex fractions. These might involve using decimal representations or other algebraic techniques.
-
How do I add more than two fractions? The principle remains the same. Find the LCD for all the denominators and convert each fraction to an equivalent fraction with that LCD before adding the numerators.
Beyond the Basics: Applications of Fraction Addition
Understanding fraction addition isn't just about solving mathematical problems; it has practical applications in various real-world scenarios. For example:
-
Cooking and Baking: Recipes often require fractional amounts of ingredients. Adding fractions is crucial for accurately scaling up or down a recipe.
-
Construction and Engineering: Many construction projects involve precise measurements, often requiring the addition of fractions for accurate calculations.
-
Finance: Understanding fractions is essential for working with percentages, interest rates, and other financial calculations.
-
Data Analysis: Fractions are frequently used to represent proportions and ratios in data analysis and statistics.
Conclusion: Mastering Fraction Addition
Adding fractions, while seemingly simple, involves a fundamental understanding of mathematical principles. Mastering this skill opens doors to solving more complex problems and applying this knowledge to diverse practical situations. The step-by-step approach detailed above, along with the understanding of the underlying mathematical principles, will equip you to confidently tackle any fraction addition problem. Remember the key: find the least common denominator, convert to equivalent fractions, add the numerators, and simplify the result if necessary. With practice, this process will become second nature. Through understanding the core concepts, you can move beyond simple calculations and apply the knowledge to more advanced mathematical concepts and real-world applications.
Latest Posts
Latest Posts
-
What Is 15 Of 45
Sep 12, 2025
-
4 1 3 Improper Fraction
Sep 12, 2025
-
What Was 21 Days Ago
Sep 12, 2025
-
72 Degree Fahrenheit To Celsius
Sep 12, 2025
-
What Is 12 5 Simplified
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about What Is 1/3 + 4/5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.